 |
В соревнованиях по легкой атлетике стартовало 15 участников. На финиш пришло 13 участников. Какова погрешность приближения?
|
|
|
|
Граница абсолютной погрешности приближенного значения числа
В практической деятельности людей постоянно встречаются как точные, так и приближенные значения величин. Числа, выражающие точные и приближенные значения величин, будем для краткости называть соответственно точными и приближенными числами. В математике нет определения точного и приближенного числа, но существуют критерии их распознавания. Приближенные числа получаются в результате измерений, при счете большого числа предметов. Всякий научный опыт и эксперимент, всякое измерение на местности или в лабораторных условиях порождают приближенные числа, так как показания различных приборов мы не можем определить точно. Поэтому мы должны научиться оценивать точность приближенных чисел и выполнять арифметические действия над ними. Знания и умения, полученные при изучении этой темы, могут пригодиться при выполнении лабораторных работ по физике, при выполнении практических работ по специальным дисциплинам, при разработке курсовых и дипломных проектов.
Буквами греческого алфавита x, y, z, … будем обозначать точные значения величин. Буквами латинского алфавита a, b, c, … будем обозначать приближенные значения величин.
x, y, z, … - точные значения величин.
a, b, c, … - приближенные значения величин.
х» a - a приближенное значение х.
Вывод: Критерии распознавания приближенных чисел: приближенные числа получаются при измерениях, при взвешиваниях, при счете большого числа предметов, при действиях с приближенными числами.
Пример:
В шестиугольнике девять диагоналей. Число 9 - точное.
Расстояние от станции Москва до станции Санкт-Петербург Октябрьской железной дороги составляет 651 км. Число 651 - приближенное, так как, с одной стороны, наши измерительные приборы не точны, с другой стороны, сами станции имеют некоторое протяжение.
|
|
|
Тормозной путь автомобиля равен расстоянию, пройденному автомобилем с момента нажатия тормоза до полной остановки автомобиля. Тормозной путь автомобиля есть величина приближенная.
Не все приближенные значения обладают одинаковой близостью к точному значению величины. Для оценки точности приближенного значения величины рассматривается разность между точным и приближенным значениями этой величины.
Определение: Разность между точным и приближенным значениями величины называется погрешностью приближенного значения этой величины.
х» a - a приближенное значение х.
х - a -погрешность приближения.
Пример:
Картридж принтера рассчитан на 800 листов. При экономном режиме удалось распечатать 830 листов. Какова погрешность приближения?
х» a;
х = 800; a = 830 - приближенное значение с избытком;
х - a = 800 - 830 = - 30; х - a = - 30; х - a < 0.
В соревнованиях по легкой атлетике стартовало 15 участников. На финиш пришло 13 участников. Какова погрешность приближения?
х» a; х = 15; a = 13 - приближенное значение с недостатком;
х - a = 15 - 13 = 2; х - a = 2; х - a > 0.
Вывод:
- Погрешность приближения может быть и положительной, и отрицательной.
- Пусть х» a.
Если a £ х, то а - приближенное значение с недостатком величины х.
Если a ³ х, то а - приближенное значение с избытком величины х.
Замечание: При вычислениях чаще не важно больше приближенное значение точного или меньше, а важно, только, на сколько они отличаются друг от друга. Поэтому на практике чаще определяют не погрешность, а абсолютную погрешность приближения.
Определение: Абсолютной погрешностью приближенного значения величины называется модуль разности между точным и приближенным значениями этой величины.
|
|
|
х» a - a приближенное значение х.
D x = | х - a | -абсолютнаяпогрешность приближения.
Вывод:
1. Абсолютнаяпогрешность приближения всегда положительна, то есть D x > 0.
2. Абсолютнаяпогрешность приближения всегда измеряется в тех же единицах, что и сама величина, то есть абсолютнаяпогрешность является размерной величиной.
Пример:
 1. х =
1. х =  D x = | х - a |
D x = | х - a |
 a = - 0,333 D x =
a = - 0,333 D x = 
D x =? D x = 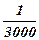
 2. p = 3,1415926… D p = | 3,1415926… - 3,14 |
2. p = 3,1415926… D p = | 3,1415926… - 3,14 |
p» 3,14 D p = 0,0015926…
D p =? 
Абсолютнаяпогрешность приближения может быть громоздкой, неудобной для вычислений (пример 1). Более того, абсолютнуюпогрешность приближения нельзя определить, если неизвестно точное значение величины (пример 2).
Вывод: Если абсолютнуюпогрешность приближения нельзя определить или абсолютнаяпогрешность приближения громоздка, то в каждом конкретном случае можно указать положительное число, которое больше или равно самой абсолютнойпогрешности.
Определение: Границей абсолютной погрешности приближения называется такое положительное число h, которое больше или равно самой абсолютнойпогрешности.
D x = | х - a | £ h
Пример: При покупке часов клиент получает свидетельство, в котором завод-изготовитель гарантирует точность суточного хода часов в пределах ± 45 секунд, что означает: часы не должны уходить вперед или отставать в сутки более чем на 45 секунд. Если при проверке купленных часов с сигналами точного времени, даваемыми по радио, обнаружилось, что часы уходят вперед в сутки на 20 секунд, то 20 секунд - абсолютная погрешность суточного хода данных часов. А число 45 секунд - граница абсолютной погрешности приближения.
Замечание:
1. В отличие от абсолютной погрешности граница абсолютной погрешности не определяется однозначно. Поэтому на практике в качестве границы абсолютной погрешности берется число, мало отличающееся от абсолютной погрешности и удобное для вычислений.
2. Если задана граница абсолютной погрешности h, то говорят, что a есть приближенное значение числа x с точностью до h, и пишут x = a ± h.
 x = a ± h Û a - h £ x £ a + h,
x = a ± h Û a - h £ x £ a + h,
a - h - нижняя границачисла x,
a + h - верхняя границачисла x.
Пример:
1. Определить границу абсолютной погрешности приближенного значения 2,7 числа е = 2,718281828459045….
D x = | х - a | ;
|
|
|
D е = | 2,718281828459045… - 2,7 | = 0,018281828459045… £ 0,02; h = 0,02;
е = 2,7 ± 0,02.
2. Электрическая сеть выдерживает напряжение U = 220 ± 3 B. Что означает эта запись? Укажите границы возможного напряжения в сети.
|
|
|


