 |
Картографические проекции. (Например: конические, цилиндрические, азимутальные, псевдоконические, псевдоцилиндрические, псевдоазимутальные, поликонические, производные (условные))
|
|
|
|
Картографическая проекция — математически определенный способ отображения поверхности эллипсоида на плоскости. Суть проекций связана с тем, что фигуру Земли — эллипсоид, не развертываемый в плоскость, заменяют на другую фигуру, развёртываемую на плоскость, или непосредственно на плоскость. При этом с эллипсоида на другую фигуру переносят сетку параллелей и меридианов. Вид этой сетки бывает разный в зависимости от того, какой фигурой заменяется эллипсоид. В любой проекции существуют искажения, они бывают четырех видов: искажения длин, искажения углов, искажения площадей, искажения форм. Искажение длин означает непостоянство масштаба плоского изображения, что проявляется в изменении масштаба от точки к точке, и даже в одной и той же точке в зависимости от направления. Масштаб на карте подписывается, но на самом деле это масштаб исходного эллипсоида, развертыванием которого в плоскость карта и получена. За характеристику искажения площадей принимают отклонение площади эллипса искажений от исходной площади на эллипсоиде. Искажения формы — графическое изображение вытянутости эллипсоида.
Конические проекции
Проектирование координатных линий Земли производят по какому-либо из законов на внутреннюю поверхность описанного или секущего конуса, а затем, разрезав конус по образующей, разворачивают его на плоскость.
Для получения нормальной прямой конической сетки делают так, чтобы ось конуса совпадала с земной осью PNР S (рис 3.2.1). 

Рисунок 3.2.1 – Коническая проекция
В этом случае меридианы изображаются прямыми линиями, исходящими из одной точки, а параллели — дугами концентрических окружностей. Если ось конуса располагают под углом к земной оси, то такие сетки называют косыми коническими.
|
|
|
В зависимости от закона, выбранного для построения параллелей, конические проекции могут быть равноугольными, равновеликими и произвольными. Конические проекции применяются для географических карт.
Цилиндрические проекции
Картографическую нормальную сетку получают путем проектирования координатных линий Земли по какому-либо закону на боковую поверхность касательного или секущего цилиндра, ось которого совпадает с осью Земли (рис.3.2.2), и последующей развертки по образующей на плоскость.


Рисунок 3.2.2 – Цилиндрическая проекция
В прямой нормальной проекции сетка получается из взаимно перпендикулярных прямых линий меридианов A, В, С, D, F, G и параллелей аа',bb',сс’ При этом без больших искажений будут изображены участки поверхности экваториальных районов, но участки полярных районов в этом случае не могут быть спроектированы.
Если повернуть цилиндр так, чтобы ось его расположилась в плоскости экватора, а поверхность его касалась полюсов, то получается поперечная цилиндрическая проекция (например, поперечная цилиндрическая проекция Гаусса). Если цилиндр поставить под другим углом к оси Земли, то получаются косые картографические сетки. На этих сетках меридианы и параллели изображаются кривыми линиями.
Азимутальные проекции
Нормальную картографическую сетку получают проектированием координатных линий Земли на так называемую картинную плоскость Q (рис. 3.2.3) — касательную к полюсу Земли. Меридианы нормальной сетки на проекции имеют вид радиальных прямых, исходящих из центральной точки проекции PN под углами, равными соответствующим углам в натуре, а параллели — концентрическими окружностями с центром в полюсе. Картинную плоскость можно располагать в любой точке земной поверхности, и точку касания называют центральной точкой проекции и принимают за зенит.
|
|
|

Рисунок 3.2.3 – Азимутальная проекция
Азимутальная проекция зависит от того, какими радиусами проводятся параллели. Подчиняя радиусы той или иной зависимости от широты, получают различные азимутальные проекции, удовлетворяющие условиям либо равноугольности, либо равновеликости.
Псевдоконические проекции
Псевдоконическими называются такие проекции, в которых параллели нормальной сетки изображаются дугами концентрических окружностей, а меридианы — кривыми линиями, симметричными относительно среднего меридиана, который изображается прямой, перпендикулярной к параллелям. Эти проекции отличаются, от конических видом меридианов. Вид картографической сетки псевдоконической проекции показан на рис. 3.2.4.
В псевдоконических проекциях линиями нулевых искажений являются средний меридиан и средняя параллель. Искажения в них нарастают по мере удаления от этих линий. Вид изокол углов в этих проекциях показан на рис. 3.2.5.
Псевдоконические проекции применяются при изображении территорий, имеющих форму ромба с вогнутыми сторонами.
Псевдоцилиндрическими называются такие проекции, в которых параллели нормальной сетки изображаются параллельными прямыми, а меридианы — кривыми линиями, симметричными относительно среднего меридиана, который изображается прямой, перпендикулярной к параллелям. Эти проекции отличаются от цилиндрических видом меридианов. В псевдоцилиндрических проекциях изоколы имеют вид сложных кривых линий, симметричных относительно экватора и среднего меридиана, причем закон нарастания искажений может быть различным.

Рисунок 3.2.4 – Картографическая сетка в псевдоконической проекции

Рисунок 3.2.5 – Изоколы углов в псевдоконической проекции
Поликонические проекции
Поликоническими называются такие проекции, в которых параллели нормальной сетки изображаются разноцентренными окружностями, а меридианы — кривыми линиями, симметричными относительно среднего меридиана, который изображается прямой, перпендикулярной к параллелям.
Поликонические проекции можно рассматривать, как проекции глобуса не на один касательный по параллели конус, а на множество касательных конусов, что обусловливает равенство масштабов проекции по всем параллелям. В этих проекциях масштаб по всем параллелям и на среднем меридиане равен единице. Искажения возрастают с удалением от среднего меридиана, и изоколы имеют вид линий, приблизительно параллельных среднему меридиану. Поэтому эти проекции более выгодно применять для изображения территорий, сильно вытянутых вдоль меридианов хотя бы от одного полюса до другого. Вид, картографической сетки в поликонической проекции показан на рис. 3.2.6.
|
|
|
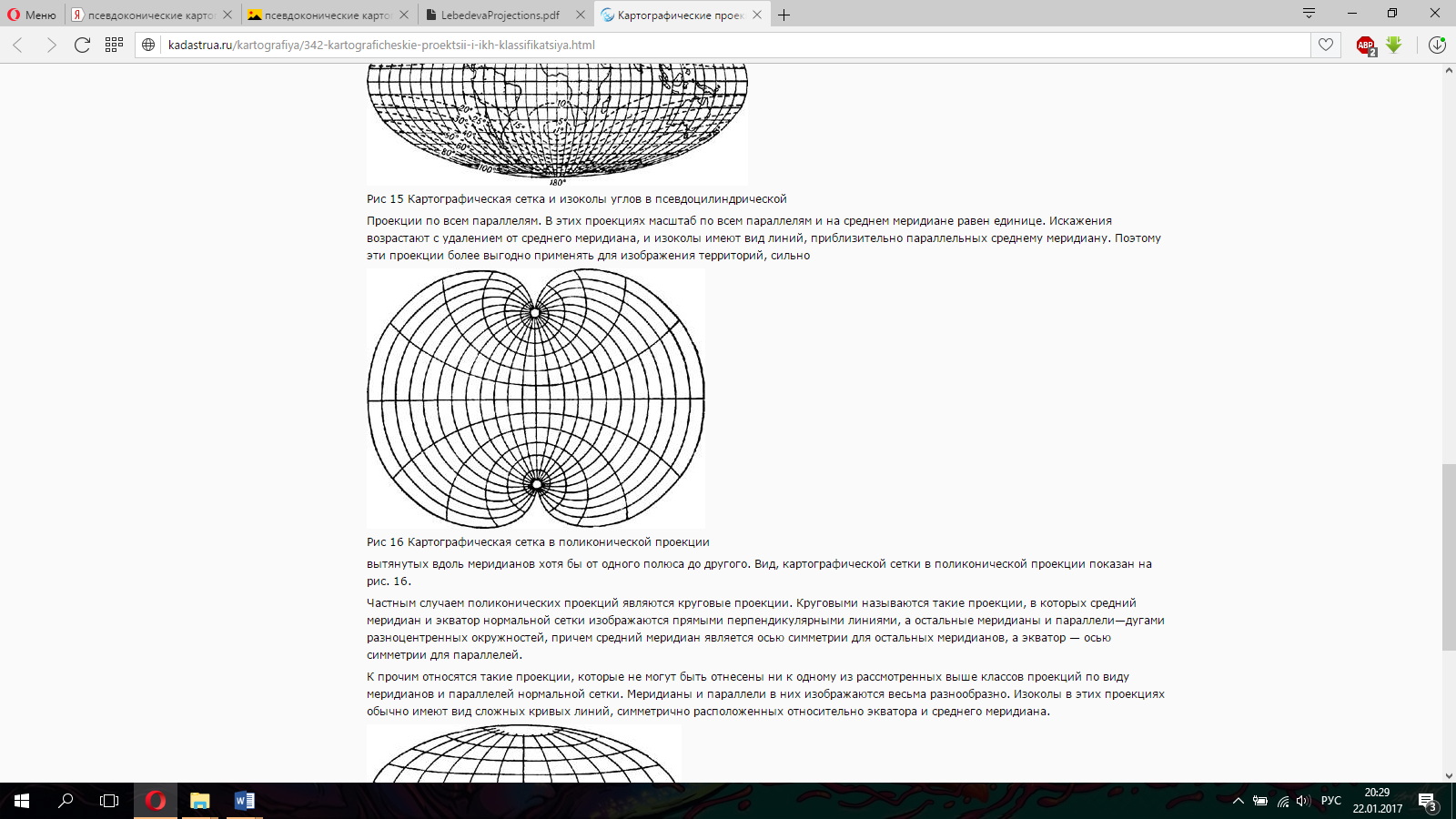
Рисунок 3.2.6 – Картографическая сетка в поликонической проекции
Частным случаем поликонических проекций являются круговые проекции. Круговыми называются такие проекции, в которых средний меридиан и экватор нормальной сетки изображаются прямыми перпендикулярными линиями, а остальные меридианы и параллели—дугами разноцентренных окружностей, причем средний меридиан является осью симметрии для остальных меридианов, а экватор — осью симметрии для параллелей.
К прочим относятся такие проекции, которые не могут быть отнесены ни к одному из рассмотренных выше классов проекций по виду меридианов и параллелей нормальной сетки. Меридианы и параллели в них изображаются весьма разнообразно. Изоколы в этих проекциях обычно имеют вид сложных кривых линий, симметрично расположенных относительно экватора и среднего меридиана. Эти проекции нашли широкое применение для мировых карт.
|
|
|


