Экспериментальная установка

Кафедра Общей и технической физики

(лаборатория виртуальных экспериментов)

ФИЗИКА

Определение теплоемкости твердых тел

Методические указания к лабораторной работе

С использованием компьютерных технологий

Для студентов бакалавриата направления

Подготовки 120700

 

 

САНКТ-ПЕТЕРБУРГ

2015

УДК 539.12

 

 

ФИЗИКА. Определение теплоемкости твердых тел. Методические указания к лабораторной работе. Фицак В.В. / Национальный минерально-сырьевой университет ”Горный”. С-Пб, 2015, 19 с.

 

Методические указания к лабораторной работе курсу «Физика», «Определение теплоемкости твердых тел», предназначены для студентов бакалавриата направления подготовки 120700 «Землеустройство и кадастры».

С помощью методических указаний студент имеет возможность, в предварительном плане, ознакомиться с физическими явлениями, методикой выполнения лабораторного исследования и правилами оформления лабораторных работ.

Выполнение лабораторных работ проводится студентом индивидуально по графику.

 

 

Табл. 5. Ил. 2. Библиогр.: 17 назв.

 

Научный редактор доц. Н.Н. Смирнова

 

© Национальный минерально-сырьевой университет ”Горный”, 2015 г.

 

 

Введение

 

В процессе обучения в вузе выполнение лабораторной работы студентами является одной из форм образовательных технологий. Она способствует формированию у студентов комплекса компетенций, таких как: способность к познавательной и творческой деятельности; способность использовать навыки работы с информацией из различных источников для решения профессиональных задач и др.

Методические указания к лабораторной работе предназначены для самостоятельной работы студентов. Они содержат основные теоретические сведения по теме, а также порядок выполнения и оформления лабораторной работы.

При выполнении лабораторной работы, студент должен понимать физический смыл данного явления или процесса рассматриваемого в лабораторной работе. Поэтому к выполнению работы целесообразно приступать только после изучения теоретического и методического материала, соответствующего данному разделу.

Кроме формирования необходимых для выпускников вуза компетенций, самостоятельное выполнение лабораторной работы способствует подготовке студентов к сдаче экзамена.

 

2. Краткое теоретическое содержание

Теплоёмкость

Теплоемкостью тела называется величина, определяемая количеством теплоты, необходимым для нагревания тела на 1° К

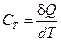(2.1)

т.е. отношение бесконечно малого количества теплоты δ Q (δ Q не является полным дифференциалом), полученного телом, к соответствующему приращению его температуры dT.

Теплоёмкость, отнесённая к единице массы вещества, называется удельной теплоёмкостью

(2.2)

Теплоёмкость, отнесённая к одному молю вещества, называется молярной теплоёмкостью

(2.3)

где m и ν – масса и число молей вещества.

Удельная и молярная теплоёмкости характеризуют уже не данное тело, а вещество, из которого тело состоит. Между вышеуказанными теплоёмкостями существуют очевидные соотношения

, (2.4)

где μ – молярная масса вещества (численно равная массе моля).

Первое начало термодинамики в дифференциальной форме

δ Q = dU+ δ А

где dU – бесконечно малое изменение внутренней энергии системы, δ А – элементарная работа, δ Q – бесконечно малое количество теплоты. В этом выражении dU является полным дифференциалом, а δ Q и δ А таковыми не являются.

Если нагревание происходит в условиях, когда объём остается постоянным (V =const), то соответствующая молярная теплоёмкость называется теплоёмкостью при постоянном объёме, или изохорической теплоёмкостью, и обозначается

. (2.5)

Так как теплота при этом тратится только на изменение внутренней энергии dU, то δ Q = dU и

. (2.6)

Отсюда dU = C_V dT и первое начало термодинамики можно записать как

. (2.7)

Следовательно, подводимое к телу тепло расходуется на изменение температуры dT (изменение внутренней энергии) и изменение объёма dV.

Если при нагревании постоянным остаётся давление, то теплоёмкость называется теплоёмкостью при постоянном давлении С_P, или изобарической теплоёмкостью

(2.8)

 

. (2.9)

 

 

Теплоёмкость твердых тел

В твердых телах частицы вещества «закреплены» в определённых положениях равновесия, отвечающих минимуму энергии взаимодействия их друг с другом. Основной формой движения, доступной таким частицам, являются колебания около положений равновесия, называемых узлами кристаллической решётки. Амплитуда этих колебаний составляет незначительную долю расстояния между атомами (≈0,05 r ₀). Рассмотрим основные теории теплоёмкости твёрдых тел.

 

Классическая модель

В основе классической теории теплоёмкости твёрдых тел (кристаллов) лежит закон равнораспределения энергии по степеням свободы. Твёрдое тело рассматривается как система N независимых друг от друга атомов, имеющих по три колебательных степени свободы. Атомы совершают тепловые колебания около положений равновесия, и если они малы, то их можно рассматривать как гармонические. На каждую степень свободы приходится в среднем энергия kT ( в виде кинетической и в виде потенциальной, k – постоянная Больцмана, T – абсолютная температура тела). Таким образом, значение полной энергии, приходящейся на одну колебательную степень свободы, равно

. (2.10)

Имея в виду, что число степеней свободы многоатомных газов 3 N – 6, (где N – число молекул, 6 – число степеней свободы поступательного и вращательного движения), то число колебательных степеней свободы равно 3 N, получим, что внутренняя энергия одного моля атомов U =3 N_A kT =3 RT, где N_A – число Авогадро, R=kN_A – универсальная газовая постоянная. Отсюда молярная теплоёмкость твёрдого тела

(2.11)

Согласно (2.11) молярная теплоёмкость всех химических простых кристаллических твёрдых тел одинакова и равна 3 R. Этот закон был установлен экспериментально Дюлонгом и Пти. Из него следует, что молярная теплоёмкость не должна зависеть ни от свойств вещества из которого состоит кристалл, ни от температуры.

Однако опыты показывают, что при обычных температурах молярная теплоёмкость большинства твёрдых тел (химических элементов) близка к значению 3 R и почти не зависит от температуры, но при низких температурах теплоёмкость убывает (рис.2.1), стремясь к нулю при по закону .

Причиной расхождения классической теории теплоёмкости является ограниченность применения закона равномерного распределения энергии теплового движения по степеням свободы. Наблюдаемая на опыте зависимость теплоёмкости от температуры может быть объяснена на основе квантовых представлений.

Модель Эйнштейна

В теории Эйнштейна твердое тело рассматривалось как система N атомов, каждый из которых является квантовым гармоническим осциллятором. Предполагалось, что колебания атомов происходят независимо друг от друга с одинаковой частотой ν. Энергия квантового гармонического осциллятора дискретна

, n = 0, 1, 2..., (2.12)

где h – постоянная Планка.

Согласно теории Эйнштейна молярная теплоёмкость кристаллической решётки определяется как

. (2.13)

При высоких температурах (kT >>h ν) выражение (2.13) переходит в (2.11), при низких температурах (kT << h ν) . Однако по теории Эйнштейна зависимость C_V (T) имеет экспоненциальный характер при , опыт даёт, что . Эти расхождения связаны с чрезмерным упрощением самой модели твёрдого тела – с предположением, что все атомы колеблются независимы друг от друга и с одинаковой частотой.

Модель Дебая

В этой модели кристаллическая решётка рассматривается как связанная система взаимодействующих атомов. Колебания такой системы – результат наложения многих гармонических колебаний с различными частотами. Под гармоническим осциллятором той или и иной частоты теперь надо понимать колебания не отдельного атома, а всей системы в целом. Задача сводится к нахождению спектра частот этих осцилляторов. Это весьма сложно. Дебай сильно упростил задачу. Он обратил внимание на то, что при низких температурах основной вклад в теплоёмкость вносят колебания низких частот, которым соответствует малые кванты энергии h ν. Низкочастотный же спектр колебаний решётки может быть рассчитан достаточно точно.

 

CV, Дж/(мольК)
	T /Θ

 

Рис. 1. Зависимость C_V (T) твердых тел от приведенной температуры T /Θ

 

Теория Дебая теплоёмкости твёрдых тел хорошо согласуется с опытом при низких температурах (при действительно ).

Для высоких температур (T >>Θ) теория Дебая приводит к закону Дюлонга и Пти, где Θ – называется характеристической температурой Дебая, и определяется из условия

. (2.15)

Согласно теории Дебая теплоёмкость определяется

, (2.16)

где , ν_max – верхняя граница возможных частот колебаний. Дебаевская температура Θуказывает для каждого твёрдого тела область температур (T< Θ), где становится существенным квантование энергии колебаний. Соотношение (2.16) не является универсальным, т.к. оно хорошо передаёт зависимость C_V(T) только для химически простых тел с простой кристаллической решёткой. К телам с более сложной структурой формула Дебая не применима. Это связано с тем, что у таких тел спектр колебаний оказывается очень сложным.

 

Теплоёмкость металлов

Металл состоит из положительно заряжённых ионов, совершающих тепловые колебания вокруг узлов кристаллической решётки. Между ними движутся так называемые свободные электроны, слабо связанные с ионами решётки. Они ведут себя подобно электронному газу. Наличием свободных электронов объясняется высокая электропроводность металлов. Классическая теория теплоёмкости не учитывает наличие электронного газа. Она учитывает тепловые колебания одних только ионов. Расчёт показывает, что отношение электронной теплоёмкости к ионной при нормальных условиях равно

, (2.17)

где ε _F – энергия Ферми при Т = 0º К. При рассматриваемых условиях kT<< ε _F, что означает, что теплоёмкость металлов за счёт свободных электронов пренебрежимо мала. При обычных температурах в тепловом движении принимает участие лишь небольшая часть свободных электронов, которые обладают энергией больше, чем ε _F, а при достаточно низких температурах теплоёмкость электронного газа превосходит ионную, поскольку последняя уменьшается ~ Т ^З.

Изложенные теории теплоёмкости твердых тел показывают, что дискретность энергетических уровней не совместима с классическим законом о равнораспределении энергии по степеням свободы. Только тогда, когда средняя энергия теплового движения kT велика по сравнению с разностями между высшими энергетическими уровнями и наинизшим из них, возбуждается много энергетических уровней. При таком условии дискретность уровней становится малосущественной, и атомная система ведет себя как классическая, в которой энергия меняется непрерывно. Отсюда следует, что чем выше температура, тем лучше оправдывается классический закон о равномерном распределении энергии по степеням свободы.

Для экспериментального определения теплоёмкости исследуемое тело помещается в калориметр, который нагревается электрическим током. Если температура калориметра с исследуемым образцом очень медленно увеличивать от начальной T ₀ на ∆T, то энергия электрического тока пойдет на нагревание образца калориметра

, (2.18)

где I и U – ток и напряжение нагревателя, τ – время нагревания, m ₀ и m – массы калориметра и исследуемого образца, c ₀, c – удельные теплоёмкости калориметра и исследуемого образца, ∆ Q – потери тепла в теплоизоляцию калориметра и в окружающее пространство.

Для исключения из уравнения (2.18) количества теплоты, расходованной на нагрев калориметра и потери теплоты в окружающее пространство, необходимо при той же мощности нагревателя нагреть пустой калориметр (без образца) от начальной температуры T ₀ на туже разность температур ∆T. Потери тепла в обоих случаях будут практически одинаковыми и очень малыми, если температура защитного кожуха калориметра в обоих случаях постоянная и равна комнатной

. (2.19)

Из уравнений (2.19) и (2.18) вытекает

. (2.20)

Уравнение (2.20) может быть использовано для экспериментального определения удельной теплоёмкости материала исследуемого образца. Изменяя температуру калориметра, необходимо построить график зависимости разности времени нагрева от изменения температуры исследуемого образца: , по угловому коэффициенту которого можно определить удельную теплоёмкость образца. Следует отметить, что в опытах по измерению теплоёмкости твёрдого тела обычно измеряют C_P. Значительно труднее обеспечить такие условия опыта, когда объём твёрдого тела оставался бы неизменным при изменении температуры. В случае твёрдого тёла изменение объёма при изменении температуры невелико и разность C_P – C_V мала, поэтому её обычно не учитывают.

 

Лабораторная работа

Цель работы

1) измерение зависимости повышения температуры исследуемого образца в муфельной печи от времени;

2) вычисление по результатам измерений теплоемкости исследуемого образца.

 

Экспериментальная установка

В работе используются: муфельная печь 1, содержащая электронагреватель 2, вентилятор обдува 3; термопара 4; цифровой термометр 5; регулируемый источник питания 6; выключатель нагрева 7; таймер 8.

 

 

 

Схема установки изображена на рисунке 1. Вентилятор обдува 3 предназначен для равномерного распределения тепла внутри печи. Электронагреватель 2 подключен к регулируемому источнику питания постоянного тока 6, контроль напряжения и тока осуществляется вольтметром и амперметром, входящими в источник питания. Для измерения температуры воздуха служит термопара 4, подключенная к цифровому термометру 5.

Порядок выполнения работы

1. Запустите лабораторную работу. Отметьте в лабораторном журнале характеристики (масса и материал) полученного образца.

2. Включите источник питания, установите напряжение, указанное преподавателем (или выбранное самостоятельно). Нагрев печи включается кнопкой "ВКЛ", расположенной на пульте НАГРЕВ только при закрытой дверце печи. Для закрывания/открывания дверцы надо нажать на нее левой кнопкой мыши.

3. Включите вентилятор обдува.

4. Не помещая исследуемый образец в печь, закройте дверцу, включите нагрев и одновременно запустите секундомер. Через интервалы времени 20¸40 секунд запишите значения температуры. Всего надо сделать 8¸10 измерений. Также запишите значения напряжения и силы тока I. Выключите нагрев, откройте дверцу печи (для ускорения остывания).

5. Для каждого интервала времени D t найдите соответствующее изменение температуры D T и посчитайте значения . Нанесите полученные точки на координатную плоскость (, t), располагая значения посередине временного интервала измерения (те есть, если измерения проводились через 30 секунд, то значение , посчитанное на интервале 0¸30 секунд соответствует времени 15 секунд). Проведите через точки прямую, продолжая ее до пересечения с осью абсцисс, определите по графику значение при t = 0, пересчитайте значение к 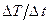. По формуле

[4]

рассчитайте собственную теплоемкость печи C_П.

6. После остывания печи поместите в нее исследуемый образец (для внесения/убирания образца надо нажать на него левой кнопкой мыши при открытой дверце).

7. Повторите измерения и вычисления по п.п. 4 и 5, изменив, если требуется, напряжение питания.

Результаты измерений занести в таблицу 1.

 

Таблица 1

Физ. величина	D t	T 1		T 2		С П	С	С о	с
Ед. измерений   Номер опыта	с	К		К
…
n

 

 

Для получения приемлемой погрешности при проведении измерений необходимо, чтобы температура повышалась не менее, чем на 3¸4 °С за интервал измерения. По формуле [4] будет определена суммарная теплоемкость печи и образца С. Найдите теплоемкость образца С_о

[5]

Рассчитайте удельную теплоемкость .

Сравните со справочными значениями удельной теплоемкости исследуемого образца.

Контрольные вопросы

1. Какая величина называется теплоемкостью вещества, удельной и молярной теплоемкостью? В каких единицах СИ они измеряются?

2. Выведите формулу для полной внутренней энергии и моля твердого тела.

3. В чем особенности теплоемкостей твердых тел? Выведите формулу для молярной теплоемкости твердого тела

4. Запишите и объясните закон Дюлонга и Пти.

5. Рассчитайте, исходя из закона Дюлонга и Пти, удельные теплоемкости алюминия ₂₃Al²⁷ и железа ₂₆Fe⁵⁶.

6. В чем заключается метод электрического нагрева для определения теплоемкости твердых тел?

7. Выведите формулу для экспериментального определения теплоемкости.

8. Основные источники ошибок данного метода измерений

 

Поделиться:

Воспользуйтесь поиском по сайту: