 |
Задания для самостоятельной работы
|
|
|
|
Лабораторная работа №121.
Перевод чисел из одной позиционной системы счисления в другую
Цель работы. Изучение методов и отработка навыков перевода чисел из одной позиционной системы счисления в другую.
Количество различных цифр 
, используемых в позиционной системе, определяет название системы счисления и называется основанием -ой системы счисления.
Любое число N в позиционной системе счисления с основанием может быть представлено в виде полинома от основания :
,
где 
— число, 
— цифры числа (коэффициенты при степенях ), — основание системы счисления ( >1).
Числа записывают в виде последовательности цифр:
. 
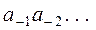, точка в последовательности отделяет целую часть числа от дробной (коэффициенты при неотрицательных степенях, от коэффициентов при отрицательных степенях). Точка опускается, если число целое (нет отрицательных степеней).
В компьютерных системах применяют позиционные системы счисления с недесятичным основанием: двоичную, восьмеричную, шестнадцатеричную.
В аппаратной основе ЭВМ лежат двухпозиционные элементы, которые могут находиться только в двух состояниях; одно из которых обозначается 0, а другое — 1. Поэтому арифметико-логической основной ЭВМ является двоичная система счисления.
Двоичная система счисления. Используется две цифры: 0 и 1. В двоичной системе любое число может быть представлено в виде: 
. 
, где 
либо 0, либо 1.
Эта запись соответствует сумме степеней числа 2, взятых с указанными коэффициентами:
Восьмеричная система счисления. Используется восемь цифр: 0, 1, 2, 3, 4, 5, 6, 7. Употребляется в ЭВМ как вспомогательная для записи информации в сокращенном виде. Для представления одной цифры восьмеричной системы используется три двоичных разряда (триада) (см. таблицу 1).
|
|
|
Шестнадцатеричная система счисления. Для изображения чисел используется 16 цифр. Первые десять цифр этой системы обозначаются цифрами от 0 до 9, а старшие шесть цифр — латинскими буквами: A (10), В (11), C (12), D (13), E (14), F (15). Шестнадцатеричная система, так же как и восьмеричная, используется для записи информации в сокращенном виде. Для представления одной цифры шестнадцатеричной системы счисления используется четыре двоичных разряда (тетрада) (см. табл. 1).
Таблица 1.
Алфавиты позиционных систем счисления (сс)
| Двоичная сс (Основание 2) | Восьмеричная сс (Основание 8) | Десятичная сс (Основание 10) | Шестнадцатеричная сс (Основание 16) | ||
| Двоичные триады | Двоичные тетрады | ||||
| A (10) B (11) C (12) D (13) E(14) F(15) |
Задание 1. Переведите числа из заданных систем счисления в десятичную систему.
Методические указания.
Перевод чисел в десятичную системуосуществляется путем составления суммы степенного ряда с основанием той системы, из которой число переводится. Затем подсчитывается значение этой суммы.
Примеры.
а) Перевести 
с.с.*
.
Ответ:. .
б) Перевести 
с.с.
.
Ответ: 
.
в) Перевести 
с.с.
.
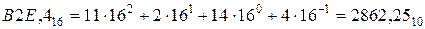Ответ: 
.
Задание 2. Переведите целые числа из десятичной системы в восьмеричную, шестнадцатеричную и двоичную системы.
Методические указания.
Перевод целых десятичных чисел в восьмеричную, шестнадцатеричную и двоичную системыосуществляется последовательным делением десятичного числа на основание той системы, в которую оно переводится, до тех пор, пока не получится частное равное нулю. Число в новой системе записывается в виде остатков от деления, начиная с последнего.
Примеры.
а) Перевести 
с.с.
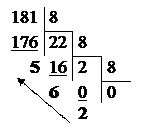
Ответ: 
.
б) Перевести 
с.с.
 |
|
|
|
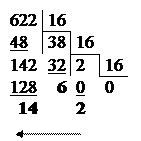Ответ: 
.
Задание 3. Переведите правильные десятичные дроби из десятичной системы в восьмеричную, шестнадцатеричную и двоичную системы.
Методические указания.
Для перевода правильной десятичной дроби в другую систему эту дробь последовательно умножают на основание той системы, в которую она переводится. При этом умножаются только дробные части полученных произведений. Если в результате умножения на некотором шагу дробная часть становится равной нулю, это означает, что получили конечную дробь в новой системе счисления. В новой системе дробь записывается в виде целых частей произведений, начиная с первого. Не все конечные дроби в результате перевода станут конечными, зачастую в новой системе счисления получается бесконечная дробь.
Примеры.
а) Перевести 
с.с.
| 0, | ´ 8 |
| 2, | ´ 8 |
 0,
| ´ 8 |
| ´ 8 | |
Условно разделим вертикальной чертой целую и
дробную часть полученных произведений.
Результат перевода – есть последовательность
цифр, состоящих из целых частей произведений,
записанная сверху вниз.
Ответ: 
.
б) Перевести с точностью до 6 знаков после запятой 
с.с.
| 0, | 65´ 2 |
| 3´ 2 | |
| 6 ´ 2 | |
| 2 ´ 2 | |
| 4 ´ 2 | |
| 8 ´ 2 | |
| 6 ´ 2 | |
| ... |
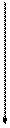0,65´2=1,3 далее умножаем дробную часть полученного произведения
0,3´2=0,6
0,6´2=1,2 каждый раз умножаем только дробную часть
произведения
0,2´2=0,4
0,4´2=0,8
0,8´2=1,6
0,6´2=1,2
Ответ: 
.
Задание 4. Переведите неправильные десятичные дроби из десятичной системы в восьмеричную, шестнадцатеричную и двоичную системы.
Методические указания.
Для перевода неправильной десятичной дроби в систему счисления с недесятичным основанием необходимо отдельно перевести целую часть и отдельно дробную.
Пример. Перевести 
с.с.
1) Переведем целую часть: 2) Переведем дробную часть:
| 22 | ||||||
| 10 | ||||||
| 4 | |||||
| 0 | ||||||
 0,
| 125  2
|
| 25 2
| |
| 5 2
| |
Получили 
; 
. Результат перевода 
.
Ответ: .
Задание 5. Переведите числа из восьмеричной и шестнадцатеричной систем счисления в двоичную систему.
|
|
|
Методические указания.
Для перевода восьмеричного или шестнадцатеричного числа в двоичную формудостаточно заменить каждую цифру этого числа соответствующим трехразрядным двоичным числом (триадой) (см. таблицу 1) или четырехразрядным двоичным числом (тетрадой) (см. таблицу 1), при этом отбрасывают незначащие нули в старших и младших (после запятой) разрядах.
Примеры.
а)   =  ;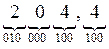
б)   =  .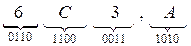
|
Задание 6. Переведите числа из восьмеричной и шестнадцатеричной систем счисления в двоичную систему.
Методические указания.
Для перехода от двоичной к восьмеричной (шестнадцатеричной) системе поступают следующим образом: двигаясь от точки влево и вправо, разбивают двоичное число на группы по три (четыре) разряда, дополняя при необходимости нулями крайние левую и правую группы. Затем триаду (тетраду) заменяют соответствующей восьмеричной (шестнадцатеричной) цифрой.
Примеры.
а) Перевести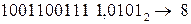 
с.с.
б) Перевести 
с.с.
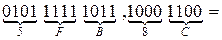
Задание 7. Переведите числа из восьмеричной в шестнадцатеричную систему счисления и из шестнадцатеричной в восьмеричную систему счисления.
Методические указания.
Перевод из восьмеричной в шестнадцатеричную систему и обратно осуществляется через двоичную систему с помощью триад и тетрад.
Пример. Перевести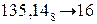 
с.с.
Ответ: 
.
Задания для самостоятельной работы
| Вари-ант | Переведите числа в 10-ю с.с. | Переведите десятичные числа в 2-ю, 8-ю и 16-ю с.с. | Восьмеричное число переведите в 16-ю с.с., а шестнадцатеричное – в 8-ю с.с. |
| 1. | 10010011111, 1012 1372,128 3CA,7D16 | 286,06 | 1263,718 2BA,2C16 |
| 2. | 11100101010, 0112 2136,318 1C3,A216 | 476,91 | 3472,628 4CA,2716 |
| 3. | 11001100111, 0112 1742,368 123E,4D16 | 438,76 | 1724,318 2АF,3C16 |
| 4. | 11101011101, 10012 1467,638 1AF,7316 | 362,87 | 1273,568 30A,E0F16 |
| 5. | 101011010110, 0012 1523,248 2А7,3Е16 | 305,37 | 1623,728 5C2,C716 |
| 6. | 11001100011, 10012 1273,568 30A,E0F16 | 324,93 | 12372,418 1D2,7D1 |
| 7. | 10011010111, 0112 1623,728 5C2,C716 | 457,21 | 1735,128 5AD,4D16 |
| 8. | 11000001111, 0112 1735,668 23A,EF16 | 343,43 | 2451,238 2BA,D316 |
| 9. | 10000111111, 10012 1327,468 3CD,BA16 | 381,93 | 1372,128 3CA,7D16 |
| 10. | 11100001101, 0112 1523,748 4BA,2F16 | 419,96 | 2136,318 1C3,A216 |
| 11. | 11011110110, 1012 4123,178 1C3,A516 | 400,01 | 1742,368 123E,4D16 |
| 12. | 110010010111, 10012 1272,128 3AD,7D16 | 153,63 | 5123,148 1B3,4D16 |
| 13. | 11100110101,10112 1071,218 5DC,F216 | 172,04 | 1263,718 2BA,2C16 |
| 14. | 10011010111, 0112 2372,128 1F2,7B16 | 191,11 | 3472,628 4CA,2716 |
| 15. | 11110010101,10012 1574,618 35C,F116 | 210,96 | 1724,318 2АF,3C16 |
| 16. | 11000011010, 10012 6123,518 13A,C216 | 229,74 | 1272,128 3AD,7D16 |
| 17. | 10011000111,11112 5412,638 52A,1716 | 248,2 | 1071,218 5DC,F216 |
| 18. | 11101101101, 10012 5123,148 1B3,4D16 | 267,72 | 2372,128 1F2,7B16 |
| 19. | 11101011001, 01012 1263,718 2BA,2C16 | 571,58 | 1742,368 123E,4D16 |
| 20. | 10101110111, 01012 3472,628 4CA,2716 | 590,72 | 1467,638 1AF,7316 |
| 21. | 10101101111, 0112 1724,318 2АF,3C16 | 495,32 | 1523,248 2А7,3Е16 |
| 22. | 11100101101,10112 1275,468 23А,Е716 | 552,5 | 1735,668 23A,EF16 |
| 23. | 10011010111, 0112 12372,418 1D2,7D1 | 533,51 | 1327,468 3CD,BA16 |
| 24. | 11011100010,11012 1735,128 5AD,4D16 | 514,58 | 1523,748 4BA,2F16 |
| 25. | 10100101111, 1012 2451,238 2BA,D316 | 609,11 | 4123,178 1C3,A516 |
|
|
|
Контрольные вопросы.
1. Как осуществляется перевод чисел из р -ой с.с. в десятичную
2. Как перевести целое десятичное число в р - ую с.с.
3. Как перевести правильную десятичную дробь в р - ую с.с.
4. Как перевести неправильную десятичную дробь в р - ую с.с.
* Здесь и в дальнейшем при одновременном использовании нескольких различных систем счисления основание системы к которой относится число будем указывать в виде нижнего индекса.
|
|
|
