 |
Лекция № 2. Отсутствующие данные
|
|
|
|
Коллектив Авторов
Базы данных: конспект лекций
Лекция № 1. Введение
Системы управления базами данных
Системы управления базами данных (СУБД) – это специализированные программные продукты, позволяющие:
1) постоянно хранить сколь угодно большие (но не бесконечные) объемы данных;
2) извлекать и изменять эти хранящиеся данные в том или ином аспекте, используя при этом так называемые запросы;
3) создавать новые базы данных, т. е. описывать логические структуры данных и задавать их структуру, т. е. предоставляют интерфейс программирования;
4) обращаться к хранящимся данным со стороны нескольких пользователей одновременно (т. е. предоставляют доступ к механизму управления транзакциями).
Соответственно, базы данных – это наборы данных, находящиеся под контролем систем управления.
Сейчас системы управления базами данных являются наиболее сложными программными продуктами на рынке и составляют его основу. В дальнейшем предполагается вести разработки по сочетанию обычных систем управления базами данных с объектно‑ориентированным программированием (ООП) и интернет‑технологиями.
Изначально СУБД были основаны на иерархических и сетевых моделях данных, т. е. позволяли работать только с древовидными и графовыми структурами. В процессе развития в 1970 г. появились системы управления базами данных, предложенные Коддом (Codd), основанные на реляционной модели данных.
Реляционные базы данных
Термин «реляционный» произошел от английского слова «relation» – «отношение».
В самом общем математическом смысле (как можно помнить из классического курса алгебры множеств) отношение – это множество
|
|
|
R = {(x 1, …, x n) | x 1 ∈ A 1 ,…,x n ∈ A n },
где A 1, …, A n – множества, образующие декартово произведение. Таким образом, отношение R – это подмножество декартова произведения множеств: A 1 × … × A n:
R ⊆ A 1 × … × A n.
Например, рассмотрим бинарные отношения строгого порядка «больше» и «меньше» на множестве упорядоченных пар чисел A 1 = A2 = {3, 4, 5}:
R > = {(3, 4), (4, 5), (3, 5)} ⊂ A 1 × A 2;
R < = {(5, 4), (4, 3), (5, 3)} ⊂ A 1 × A 2.
Эти же отношения можно представить в виде таблиц.
Отношение «больше» R >:

Отношение «меньше» R <:

Таким образом, мы видим, что в реляционных базах данных самые различные данные организовываются в виде отношений и могут быть представлены в форме таблиц.
Нужно заметить, что эти два рассмотренных нами отношения R > и R < не эквивалентны между собой, другими словами, таблицы, соответствующие этим отношениям, не равны друг другу.
Итак, формы представления данных в реляционных БД могут быть разными. В чем проявляется эта возможность различного представления в нашем случае? Отношения R > и R < – это множества, а множество – структура неупорядоченная, значит, в таблицах, соответствующих этим отношениям, строки можно менять между собой местами. Но в то же время элементы этих множеств – это упорядоченные наборы, в нашем случае – упорядоченные пары чисел 3, 4, 5, значит, столбцы менять местами нельзя. Таким образом, мы показали, что представление отношения (в математическом смысле) в виде таблицы с произвольным порядком строк и фиксированным числом столбцов является приемлемой, правильной формой представления отношений.
Но если рассматривать отношения R > и R < с точки зрения заложенной в них информации, то понятно, что они эквивалентны. Поэтому в реляционных базах данных понятие «отношение» имеет несколько другой смысл, нежели отношение в общей математике. А именно оно не связано с упорядоченностью по столбцам в табличной форме представления. Вместо этого вводятся так называемые схемы отношений «строка – заголовок столбцов», т. е. каждому столбцу дается заголовок, после чего их можно беспрепятственно менять местами.
|
|
|
Вот как будут выглядеть наши отношения R > и R < в реляционной базе данных.
Отношение строгого порядка (вместо отношения R >):

Отношение строгого порядка (вместо отношения R <):

Обе таблицы‑отношения получают новое (в данном случае одинаковое, так как введением дополнительных заголовков мы стерли различия между отношениями R > и R <) название.
Итак, мы видим, что при помощи такого несложного приема, как дополнение таблиц необходимыми заголовками, мы приходим к тому, что отношения R > и R < становятся эквивалентными друг другу.
Таким образом, делаем вывод, что понятие «отношение» в общем математическом и в реляционном смысле совпадают не полностью, не являются тождественными.
В настоящее время реляционные системы управления базами данных составляют основу рынка информационных технологий. Дальнейшие исследования ведутся в направлении сочетания той или иной степени реляционной модели.
Лекция № 2. Отсутствующие данные
В системах управления базами данных для определения отсутствующих данных описаны два вида значений: пустые (или Empty‑значения) и неопределенные (или Null‑значения).
В некоторой (преимущественно коммерческой) литературе на Null‑значения иногда ссылаются как на пустые или нулевые значения, однако это неверно. Смысл пустого и неопределенного значения принципиально различается, поэтому необходимо внимательно следить за контекстом употребления того или иного термина.
1. Пустые значения (Empty‑значения)
Пустое значение – это просто одно из множества возможных значений какого‑то вполне определенного типа данных.
Перечислим наиболее «естественные», непосредственные пустые значения (т. е. пустые значения, которые мы могли бы выделить самостоятельно, не имея никакой дополнительной информации):
1) 0 (нуль) – нулевое значение является пустым для числовых типов данных;
2) false (неверно) – является пустым значением для логического типа данных;
|
|
|
3) B’’ – пустая строка бит для строк переменной длины;
4) “” – пустая строка для строк символов переменной длины.
В приведенных выше случаях определить, пустое значение или нет, можно путем сравнивания имеющегося значения с константой пустого значения, определенной для каждого типа данных. Но системы управления базами данных в силу реализованных в них схем долговременного хранения данных могут работать только со строками постоянной длины. Из‑за этого пустой строкой бит можно назвать строку двоичных нулей. Или строку, состоящую из пробелов или каких‑либо других управляющих символов, – пустой строкой символов.
Вот несколько примеров пустых строк постоянной длины:
1) B’0’;
2) B’000’;
3) ‘ ‘.
Как же в этих случаях определить, является ли строка пустой?
В системах управления базами данных для проверки на пустоту применяется логическая функция, т. е. предикат IsEmpty (<выражение>), что буквально означает «есть пустой». Этот предикат обычно встроен в систему управления базами данных и может применяться к выражению абсолютно любого типа. Если такого предиката в системах управления базами данных нет, то можно написать логическую функцию самим и включить ее в список объектов проектируемой базы данных.
Рассмотрим еще один пример, когда не так просто определить, пустое ли мы имеем значение. Данные типа «дата». Какое значение в этом типе считать пустым значением, если дата может варьироваться в диапазоне от 01.01.0100. до 31.12.9999? Для этого в СУБД вводится специальное обозначение для константы пустой даты {…}, если значения этого типа записывается: {ДД. ММ. ГГ} или {ГГ. ММ. ДД}. С этим значением и происходит сравнение при проверке значения на пустоту. Оно считается вполне определенным, «полноправным» значением выражения этого типа, причем наименьшим из возможных.
При работе с базами данных пустые значения часто используются как значения по умолчанию или применяются, если значения выражений отсутствуют.
2. Неопределенные значения (Null‑значения)
|
|
|
Слово Null используется для обозначения неопределенных значений в базах данных.
Чтобы лучше понять, какие значения понимаются под неопределенными, рассмотрим таблицу, являющуюся фрагментом базы данных:

Итак, неопределенное значение или Null‑значение – это:
1) неизвестное, но обычное, т. е. применимое значение. Например, у господина Хайретдинова, который является номером один в нашей базе данных, несомненно, имеются какие‑то паспортные данные (как у человека 1980 г. рождения и гражданина страны), но они не известны, следовательно, не занесены в базу данных. Поэтому в соответствующую графу таблицы будет записано значение Null;
2) неприменимое значение. У господина Карамазова (№ 2 в нашей базе данных) просто не может быть никаких паспортных данных, потому что на момент создания этой базы данных или внесения в нее данных, он являлся ребенком;
3) значение любой ячейки таблицы, если мы не можем сказать применимое оно или нет. Например, у господина Коваленко, который занимает третью позицию в составленной нами базе данных, неизвестен год рождения, поэтому мы не можем с уверенностью говорить о наличие или отсутствии у него паспортных данных. А следовательно, значениями двух ячеек в строке, посвященной господину Коваленко будет Null‑значение (первое – как неизвестное вообще, второе – как значение, природа которого неизвестна). Как и любые другие типы данных, Null‑значения тоже имеют определенные свойства. Перечислим самые существенные из них:
1) с течением времени понимание Null‑значения может меняться. Например, у господина Карамазова (№ 2 в нашей базе данных) в 2014 г., т. е. по достижении совершеннолетия, Null‑значение изменится на какое‑то конкретное вполне определенное значение;
2) Null‑значение может быть присвоено переменной или константе любого типа (числового, строкового, логического, дате, времени и т. д.);
3) результатом любых операций над выражениями с Null‑значе‑ниями в качестве операндов является Null‑значение;
4) исключением из предыдущего правила являются операции конъюнкции и дизъюнкции в условиях законов поглощения (подробнее о законах поглощения смотрите в п. 4 лекции № 2).
3. Null‑значения и общее правило вычисления выражений
Поговорим подробнее о действиях над выражениями, содержащими Null‑значения.
Общее правило работы с Null‑значениями (то, что результат операций над Null‑значениями есть Null‑значение) применяется к следующим операциям:
1) к арифметическим;
2) к побитным операциям отрицания, конъюнкции и дизъюнкции (кроме законов поглощения);
|
|
|
3) к операциям со строками (например, конкотинации – сцепления строк);
4) к операциям сравнения (<, ≤, ≠, ≥, >).
Приведем примеры. В результате применений следующих операций будут получены Null‑значения:
3 + Null, 1/ Null, (Иванов' + '' + Null) ≔ Null
Здесь вместо обычного равенства использована операция подстановки «≔» из‑за особого характера работы с Null‑значениями. Далее в подобных ситуациях также будет использоваться этот символ, который означает, что выражение справа от символа подстановки может заменить собой любое выражение из списка слева от символа подстановки.
Характер Null‑значений приводит к тому, что часто в некоторых выражениях вместо ожидаемого нуля получается Null‑значение, например:
(x – x), y * (x – x), x * 0 ≔ Null при x = Null.
Все дело в том, что при подстановке, например, в выражение (x – x) значения x = Null, мы получаем выражение (Null – Null), и в силу вступает общее правило вычисления значения выражения, содержащего Null‑значения, и информация о том, что здесь Null‑значение соответствует одной и той же переменной теряется.
Можно сделать вывод, что при вычислении любых операций, кроме логических, Null‑значения интерпретируются как неприменимые, и поэтому в результате получается тоже Null‑значение.
К не менее неожиданным результатам приводит использование Null‑значений в операциях сравнения. Например, в следующих выражениях также получаются Null‑значения вместо ожидаемых логических значений True или False:
(Null < Null); (Null ≤ Null); (Null = Null); (Null ≠ Null);
(Null > Null); (Null ≥ Null) ≔ Null;
Таким образом, делаем вывод, что нельзя говорить о том, что Null‑значение равно или не равно самому себе. Каждое новое вхождение Null‑значения рассматривается как независимое, и каждый раз Null‑значения воспринимаются как различные неизвестные значения. Этим Null‑значения кардинально отличаются от всех остальных типов данных, ведь мы знаем, что обо всех пройденных ранее величинах и их типах с уверенностью можно было говорить, что они равны или не равны друг другу.
Итак, мы видим, что Null‑значения не являются значениями переменных в обычном смысле этого слова. Поэтому становится невозможным сравнивать значения переменных или выражения, содержащие Null‑значения, поскольку в результате мы будем получать не логические значения True или False, а Null‑значения, как в следующих примерах:
(x < Null); (x ≤ Null); (x = Null); (x ≠ Null); (x > Null);
(x ≥ Null) ≔ Null;
Поэтому по аналогии с пустыми значениями для проверки выражения на Null‑значения необходимо использовать специальный предикат:
IsNull (<выражение>), что буквально означает «есть Null».
Логическая функция возвращает значение True, если в выражении присутствует Null или оно равно Null, и False – в противном случае, но никогда не возвращает значение Null. Предикат IsNull может применяться к переменным и выражению любого типа. Если применять его к выражениям пустого типа, предикат всегда будет возвращать False.
Например:

Итак, действительно, видим, что в первом случае, когда предикат IsNull взяли от нуля, на выходе получилось значение False. Во всех случаях, в том числе во втором и третьем, когда аргументы логической функции оказались равными Null‑значению, и в четвертом случае, когда сам аргумент и был изначально равен Null‑значению, предикат выдал значение True.
4. Null‑значения и логические операции
Обычно в системах управления базами данных непосредственно поддерживаются только три логические операции: отрицание, конъюнкция & и дизъюнкция ∨. Операции следования ⇒ и равносильности ⇔ выражаются через них с помощью подстановок:
(x ⇒ y) ≔ (x ∨ y);
(x ⇔ y) ≔ (x ⇒ y) & (y ⇒ x);
Заметим, что эти подстановки полностью сохраняются и при использовании Null‑значений.
Интересно, что при помощи операции отрицания «» любая из операций конъюнкция & или дизъюнкция ∨ может быть выражена одна через другую следующим образом:
(x & y) ≔ (x ∨ y);
(x ∨ y) ≔ (x & y);
На эти подстановки, как и на предыдущие, Null‑значения влияния не оказывают.
А теперь приведем таблицы истинности логических операций отрицания, конъюнкции и дизъюнкции, но кроме привычных значений True и False, используем также Null‑значение в качестве операндов. Для удобства введем следующие обозначения: вместо True будем писать t, вместо False – f, а вместо Null – n.
1. Отрицание x.

Стоит отметить следующие интересные моменты касательно операции отрицания с использованием Null‑значений:
1) x ≔ x – закон двойного отрицания;
2) Null ≔ Null – Null‑значение является неподвижной точкой.
2. Конъюнкция x & y.
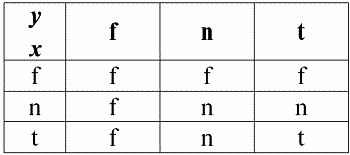
Эта операция также имеет свои свойства:
1) x & y ≔ y & x – коммутативность;
2) x & x ≔ x – идемпотентность;
3) False & y ≔ False, здесь False – поглощающий элемент;
4) True & y ≔ y, здесь True – нейтральный элемент.
3. Дизъюнкция x ∨ y.

Свойства:
1) x ∨ y ≔ y ∨ x – коммутативность;
2) x ∨ x ≔ x – идемпотентность;
3) False ∨ y ≔ y, здесь False – нейтральный элемент;
4) True ∨ y ≔ True, здесь True – поглощающий элемент.
Исключение из общего правила составляют правила вычисления логических операций конъюнкция & и дизъюнкция ∨ в условиях действия законов поглощения:
(False & y) ≔ (x & False) ≔ False;
(True ∨ y) ≔ (x ∨ True) ≔ True;
Эти дополнительные правила формулируются для того, чтобы при замене Null‑значения значениями False или True результат бы все равно не зависел бы от этого значения.
Как и ранее было показано для других типов операций, применение Null‑значений в логических операциях могут также привести к неожиданным значениям. Например, логика на первый взгляд нарушена в законе исключения третьего (x ∨ x) и в законе рефлексивности (x = x), поскольку при x ≔ Null имеем:
(x ∨ x), (x = x) ≔ Null.
Законы не выполняются! Объясняется это так же, как и раньше: при подстановке Null‑значения в выражение информация о том, что это значение сообщается одной и той же переменной теряется, а в силу вступает общее правило работы с Null‑значениями.
Таким образом, делаем вывод: при выполнении логических операций с Null‑значениями в качестве операнда эти значения определяются системами управления базами данных как применимое, но неизвестное.
5. Null‑значения и проверка условий
Итак, из всего вышесказанного можно сделать вывод, что в логике систем управления базами данных имеются не два логических значения (True и False), а три, ведь Null‑значение также рассматривается как одно из возможных логических значений. Именно поэтому на него часто ссылаются как на неизвестное значение, значение Unknown.
Однако, несмотря на это, в системах управления базами данных реализуется только двузначная логика. Поэтому условие с Null‑значением (неопределенное условие) должно интерпретироваться машиной либо как True, либо как False.
В языке СУБД по умолчанию установлено опознавание условия с Null‑значением как значения False. Проиллюстрируем это следующими примерами реализации в системах управления базами данных условных операторов If и While:
If P then A else B;
Эта запись означает: если P принимает значение True, то выполняется действие A, а если P принимает значение False или Null, то выполняется действие B.
Теперь применим к этому оператору операцию отрицания, получим:
If P then B else A;
В свою очередь, этот оператор означает следующее: если P принимает значение True, то выполняется действие B, а в том случае, если P принимает значение False или Null, то будет выполняться действие A.
И снова, как мы видим, при появлении Null‑значения мы сталкиваемся с неожиданными результатами. Дело в том, что два оператора If в этом примере не эквивалентны! Хотя один из них получен из другого отрицанием условия и перестановкой ветвей, т. е. стандартной операцией. Такие операторы в общем случае эквивалентны! Но в нашем примере мы видим, что Null‑значению условия P в первом случае соответствует команда B, а во втором – A.
А теперь рассмотрим действие условного оператора While:
While P do A; B;
Как работает этот оператор? Пока переменная P имеет значение True, будет выполняться действие A, а как только P примет значение False или Null, выполнится действие B.
Но не всегда Null‑значения интерпретируются как False. Например, в ограничениях целостности неопределенные условия опознаются как True (ограничения целостности – это условия, накладываемые на входные данные и обеспечивающие их корректность). Это происходит потому, что в таких ограничениях отвергнуть нужно только заведомо ложные данные.
И опять‑таки в системах управления базами данных существует специальная функция подмены IfNull (ограничения целостности, True), с помощью которой Null‑значения и неопределенные условия можно представить в явном виде.
Перепишем условные операторы If и While с использованием этой функции:
1) If IfNull (P, False) then A else B;
2) While IfNull (P, False) do A; B;
Итак, функция подмены IfNull (выражение 1, выражение 2) возвращает значение первого выражения, если оно не содержит Null‑значения, и значение второго выражения – в противном случае.
Надо заметить, что на тип возвращаемого функцией IfNull выражения никаких ограничений не накладывается. Поэтому с помощью этой функции можно явно переопределить любые правила работы с Null‑значениями.
|
|
|


