 |
Нахождение длины дуги кривой
|
|
|
|
Введение
Нахождение производной f’ (x) или дифференциала df=f’ (x) dx функции f(x) является основной задачей дифференциального исчисления. В интегральном исчислении решается обратная задача: по заданной функции f(x) требуется найти такую функцию F(x), что F’ (х)=f(x) или F(x)=F’ (x) dx=f(x) dx. Таким образом, основной задачей интегрального исчисления является восстановление функции F(x) по известной производной (дифференциалу) этой функции. Интегральное исчисление имеет многочисленные приложения в геометрии, механике, физике и технике. Оно дает общий метод нахождения площадей, объемов, центров тяжести и т.д.
Курс математического анализа содержит разнообразный материал, однако, одним из его центральных разделов является определенный интеграл. Интегрирование многих видов функций подчас представляет собой одну из труднейших проблем математического анализа.
Вычисление определенного интеграла имеет не только теоретический интерес. К его вычислению сводятся иногда задачи, связанные с практической деятельностью человека.
Также понятие определенного интеграла широко используется в физике.
Нахождение площади криволинейной трапеции
Криволинейной трапецией называется фигура, расположенная в прямоугольной системе координат и ограниченная осью абсцисс, прямыми х = а и х = b и кривой  , причем
, причем  неотрицательна на отрезке
неотрицательна на отрезке  . Приближенно площадь криволинейной трапеции можно найти так:
. Приближенно площадь криволинейной трапеции можно найти так:
1. разделить отрезок  оси абсцисс на n равных отрезков;
оси абсцисс на n равных отрезков;
2. провести через точки деления отрезки, перпендикулярные к оси абсцисс, до пересечения с кривой  ;
;
3. заменить получившиеся столбики прямоугольниками с основанием  и высотой, равной значению функции f в левом конце каждого отрезка;
и высотой, равной значению функции f в левом конце каждого отрезка;
|
|
|
4. найти сумму площадей этих прямоугольников.
Но можно найти площадь криволинейной иначе: по формуле Ньютона-Лейбница. Для доказательства формулы, носящей их имена, докажем, что площадь криволинейной трапеции равна  , где – любая из первообразных функции
, где – любая из первообразных функции  , график которой ограничивает криволинейную трапецию.
, график которой ограничивает криволинейную трапецию.
Вычисление площади криволинейной трапеции записывается так:
1. находится любая из первообразных  функции
функции  .
.
2. записывается  .
.  - это формула Ньютона-Лейбница.
- это формула Ньютона-Лейбница.
Нахождение площади криволинейного сектора
 http://webmath.exponenta.ru/s/c/function/content/chapter3/section4/paragraph4/03040401.jpg
1 http://webmath.exponenta.ru/s/c/function/content/chapter3/section4/paragraph4/03040401.jpg
1
|
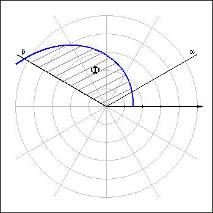
| Площадь криволинейного сектора. |
Рассмотрим кривую ρ = ρ (φ) в полярной системе координат, где ρ (φ) – непрерывная и неотрицательная на [α; β] функция. Фигура, ограниченная кривой ρ (φ) и лучами φ = α, φ = β, называется криволинейным сектором. Площадь криволинейного сектора равна

|
Нахождение длины дуги кривой
Прямоугольные координаты
Пусть в прямоугольных координатах дана плоская кривая AB, уравнение которой y = f(x), где a ≤ x ≤ b. (рис 2) [7]
Под длиной дуги AB понимается предел, к которому стремиться длина ломаной линии, вписанной в эту дугу, когда число звеньев ломаной неограниченно возрастает, а длина наибольшего звена ее стремиться к нулю.
Применим схему I (метод сумм).
Точками X  = a, X
= a, X  , …, X
, …, X  = b (X
= b (X  ≤ X
≤ X  ≤ … ≤ X
≤ … ≤ X  ) разобьем отрезок [a, b] на n частей. Пусть этим точкам соответствуют точки M
) разобьем отрезок [a, b] на n частей. Пусть этим точкам соответствуют точки M  = A, M
= A, M  , …, M
, …, M  = B на кривой AB. Проведем хорды M
= B на кривой AB. Проведем хорды M  M
M  , M
, M  M
M  , …, M
, …, M  M
M  , длины которых обозначим соответственно через ΔL
, длины которых обозначим соответственно через ΔL  , ΔL
, ΔL  , …, ΔL
, …, ΔL  .
.
|

Получим ломанную M  M
M  M
M  … M
… M  M
M  , длина которой равна L
, длина которой равна L  = ΔL
= ΔL  + ΔL
+ ΔL  + … + ΔL
+ … + ΔL  =
=  ΔL
ΔL  .
.
Длину хорды (или звена ломанной) ΔL  можно найти по теореме Пифагора из треугольника с катетами ΔX
можно найти по теореме Пифагора из треугольника с катетами ΔX  и ΔY
и ΔY  :
:
ΔL  =
=  , где ΔX
, где ΔX  = X
= X  – X
– X  , ΔY
, ΔY  = f(X
= f(X  ) – f(X
) – f(X  ).
).
|
|
|
По теореме Лагранжа о конечном приращении функции
ΔY  =
=  (C
(C  ) ΔX
) ΔX  , где C
, где C 
 (X
(X  , X
, X  ).
).
Поэтому
ΔL  =
=  =
=  ,
,
а длина всей ломанной M  M
M  M
M  … M
… M  M
M  равна
равна
L  =
=  ΔL
ΔL  =
= 
 .
.
Длина кривой AB, по определению, равна
L =  L
L  =
= 
 ΔL
ΔL  .
.
Заметим, что при ΔL 
 0 также и ΔX
0 также и ΔX 
 0 (ΔL
0 (ΔL  =
=  и следовательно | ΔX
и следовательно | ΔX  | < ΔL
| < ΔL  ). Функция
). Функция  непрерывна на отрезке [a, b], так как, по условию, непрерывна функция f
непрерывна на отрезке [a, b], так как, по условию, непрерывна функция f  (X). Следовательно, существует предел интегральной суммы L
(X). Следовательно, существует предел интегральной суммы L  =
=  ΔL
ΔL  =
= 
 , кода max ΔX
, кода max ΔX 
 0:
0:
L = 

 =
= 
 dx.
dx.
Таким образом, L = 
 dx.
dx.
Пример: Найти длину окружности радиуса R. (рис 3)

|
Найдем ¼ часть ее длины от точки (0; R) до точки (R; 0). Так как
y =  , ¼L =
, ¼L = 
 dx = R arcsin
dx = R arcsin 
 = R
= R  .
.
Значит L = 2  R.
R.
Полярные координаты
Пусть кривая AB задана уравнением в полярных координатах r = r( ),
),  . Предположим, что r(
. Предположим, что r( ) и r
) и r  (
( ) непрерывны на отрезке [
) непрерывны на отрезке [  ].
].
Если в равенствах x = r cos  , y = r sin
, y = r sin  , связывающих полярные и декартовы координаты, параметром считать угол
, связывающих полярные и декартовы координаты, параметром считать угол  , то кривую AB можно задать параметрически
, то кривую AB можно задать параметрически

Тогда

Поэтому
 =
= 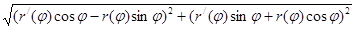 =
= 
Применяя формулу L = 
 ,
,
получаем L = 


|
Пример:Найти длину кардиоиды r = a (1 + cos  ). (рис. 4)
). (рис. 4)
Решение:Кардиоида r = a (1 + cos  ) симметрична относительно полярной оси. Найдем половину (рис 4) длины кардиоиды:
) симметрична относительно полярной оси. Найдем половину (рис 4) длины кардиоиды:
½ L = 
 =a
=a 
 =a
=a 
 = 2a
= 2a  cos
cos  d
d  = 4a sin
= 4a sin 
 = 4a.
= 4a.
Нахождение объема тел
Вычисление объема тела по известным площадям параллельных сечений
Пусть требуется найти объем V тела (рис 5), причем известны площади сечений этого тела плоскостями, перпендикулярными некоторой оси, например оси Ox: S = S (x), a ≤ x ≤ b [5]
Применим схему II (метод дифференциала).
|

1. Через произвольную точку x  [а; b]проведем плоскость П, перпендикулярную оси Ох. Обозначим через S (x) площадь сечения тела этой плоскостью; S (x) считаем известной и непрерывно изменяющейся при изменении x. Через v (x) обозначим объем части тела, лежащее левее плоскости П. Будем считать, что на отрезке [а; x]величина v есть функция от x, т.е. v = у(x) (v(a) = 0, v(b) = V).
[а; b]проведем плоскость П, перпендикулярную оси Ох. Обозначим через S (x) площадь сечения тела этой плоскостью; S (x) считаем известной и непрерывно изменяющейся при изменении x. Через v (x) обозначим объем части тела, лежащее левее плоскости П. Будем считать, что на отрезке [а; x]величина v есть функция от x, т.е. v = у(x) (v(a) = 0, v(b) = V).
2. Находим дифференциал dV функции v = v(x). Он представляет собой
«элементарный слой» тела, заключенный между параллельными плоскостями, пересекающими ось Ох в точках x и x + Δx, который приближенно может быть принят за цилиндр с основанием S (x) и высотой dx. Поэтому дифференциал объема dV = S (х) d х.
|
|
|
3. Находим искомую величину V путем интегрирования d А в пределах от a до b:
V =  S (x) dx
S (x) dx
Формула объема тела по площади параллельных сечений
Пример:Найти объем эллипсоида  (рис 6) [5]
(рис 6) [5]
|

Решение: Рассекая эллипсоид плоскостью, параллельной плоскости OYZ и на расстоянии х от нее (- a ≤ x ≤ b.), получим эллипс

Площадь этого эллипса равна S(x) =  bc (1 –
bc (1 –  ). Поэтому, по формуле имеем
). Поэтому, по формуле имеем
V =  bc
bc  (1 –
(1 –  ) dx =
) dx = 
 a bc.
a bc.
Объём тела вращения
Пусть вокруг оси Ох вращается криволинейная трапеция, ограниченная непрерывной линией у = f (х) ≥ 0, отрезком а ≤ х ≤ b и прямыми х = а и х = b (рис 7). Полученная от вращения фигура называется телом вращения. Сечение этого тела плоскостью, перпендикулярной оси Ох, проведенной через произвольную точку х оси O х), есть круг с радиусом у = f (х). Следовательно, S (x)=  y
y  .
.
Применяя формулу
V =  S (x) dx
S (x) dx
объема тела по площадипараллельных сечений, получаем


V  =
= 
 y
y  dx.
dx.
Если криволинейная трапеция ограничена графиком непрерывной функции x =  (x) ≥ 0 и прямыми x = 0, y = c, y = d (c <
(x) ≥ 0 и прямыми x = 0, y = c, y = d (c <
d), то объем тела, образованного вращением этой трапеции вокруг оси Оу, по аналогии с формулой
V =  S(x) dx,
S(x) dx,
равен
V = 
 x
x  dy.
dy.
Пример:Найти объем тела, образованного вращением фигуры, ограниченной линиями у =  , x = 0, у = 2
, x = 0, у = 2 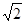 вокруг оси Оу. [5]
вокруг оси Оу. [5]
Решение: По формуле
V = 
 x
x  dy.
dy.
находим:
V  =
= 
 2ydy =
2ydy =  y
y 
 = 8
= 8  .
.
|
|
|


