Виды отношений между понятиями

Для того, чтобы правильно оперировать понятиями — в этом состоит одна из целей изучения теории понята — необходимо учитывать, что они существуют в системе знания не изолированно, а находятся в каких-то отношениях между собой. Эти отношения многообразны. Можно выделить, по крайней мере, два типа таких отношений. Один тип - - ношения теоретико-множес т венной (экстенсиональной) природы. Это отношения между классами, которые представляют объемы понятий, хотя и зависят определенным образом от содержаний понятий. Другого типа отношения возникают в процессе познания, когда возникают вопросы: может ли быть познано одно явление, если не познано другое? знание каких явлений необходимо для познания других? и соответственно о том, какие понятия необходимы, и даже в какой степени, для определения других? и что необходимо для определения первых?

Примером такой субординации понятий может служить определение истинных солнечных суток: «Истинные солнечные сутки — это промежуток времени между двумя непосредственно следующими друг за другом истинными полуднями. Истинный полдень (в данном месте) — это момент верхней кульминации центра солнечного диска (светила вообще). Кульминация центра солнечного диска — это явление прохождения центра диска Солнца через небесный меридиан, а верхняя кульминация — это прохождение центра диска через меридиан верхней части небесной сферы. Небесный меридиан — это линия, в которой плоскость небесного меридиана пересекает небесную сферу. Плоскость небесного меридиана — это плоскость, проходящая через точку зенита центра небесной сферы и полюс мира. Точка зенита — это наивысшая точка небесной сферы над головой наблюдателя. Полюсы мира — это точки пересечения оси мира с небесной сферой. Ось мира — это ось суточного вращения небесной сферы. Центр небесной сферы — это глаз наблюдателя. Небесная сфера — это воображаемая шаровая поверхность, на которую мы проецируем положение небесных тел. Верхняя часть небесной сферы — это часть небесной сферы, лежащая на плоскости небесного экватора. Плоскость небесного экватора — это плоскость, перпендикулярная оси мира и проходящая через центр небесной сферы».

Однако в логике пока нет теории, описывающей отношения этого (последнего) типа. Но довольно детально разработана теория отношений первого типа. Мы ограничимся рассмотрением только этих отношений.

Здесь имеются в виду отношения между парами понятий по их содержаниям и по их объемам. Те и другие отношения, как мы увидим далее, определенным образом связаны между собой. Выяснение отношений между содержаниями может быть связано с вопросами: является ли содержание одного понятия более широким, чем содержание другого, или, могут ли признаки, составляющие содержание одного и другого, принадлежать одним и тем же предметам? Об объемах двух понятий соответственно можно спросить: является ли объем одного понятия уже объема другого, или, имеются ли такие предметы, которые одновременно являются элементами объема и одного, и другого понятия?

Обратим внимание сразу на то, что надо отличать отно шения понятий о тех или иных предметах от отношений между самими предметами, тем более что имеются даже об щие термины для обозначения отношений того и другого типа. Так, мы говорим, что крыло самолета является частью самолета, а объем понятия «реактивный самолет» является частью объема понятия «самолет». Городской район — часть города, но объем понятия «городской район», конечно, не является частью объема понятия «город». Отношения «часть» — «целое» между предметами называются мерно- логическими; рассматриваемые здесь отношения между понятиями — это логические отношения (при этом опреде ленного типа, связанные именно с указанными выше вопро сами. Возможны и другие отношения: например, в системе понятий той или иной науки одни понятия определимы че рез другие, но не наоборот и т. д.).

Однако и среди интересующих нас отношений между понятиями возможно различение отношений по логическим и фактическим содержаниям и соответственно объемам. В дальнейшем речь будет идти об отношениях между фактическими содержаниями (и объемами) относительно всех вообще имеющихся на данный момент знаний в повседневном обиходе или в соответствующей науке, к которой относится понятие.

Кроме того, надо заметить, что в практике научного познания возникают ситуации, когда надо определить отношения между множеством понятий, состоящим из более чем двух понятий. Но задача в этом случае сводится к более простой: к выяснению отношений данного множества понятий попарно.

I. Любые два понятия прежде всего являются сравнимыми или н е с р а в н и м ы м и. Два понятия сравнимы, если они имеют общий род. В противном случае понятия несравнимы. Например, понятия «плоская геометрическая фигура (род), замкнутая и ограниченная четырьмя прямыми (видовое отличие)» и «плоская геометрическая фигура (род), замкнутая и ограниченная тремя прямыми (видовое отличие)» являются сравнимыми. Но «плоская, замкнутая геометрическая фигура (род), ограниченная четырьмя сторонами», не является сравнимым понятием ни с одним из указанных. Обратим внимание на то, что обычно сравнимыми называют понятия, предметы которых имеют какие-то общие признаки, если же у предметов, мыслимых в понятии, нет никаких общих признаков, то они несравнимы. Однако, строго говоря, все предметы, поскольку понятие «предмет» употребляется здесь в широком смысле «как предмет мысли», имеют какие-то общие признаки, хотя бы именно тот, что они являются или могут быть предметами мысли. Кажутся явно несравнимыми, например, понятия «радость» и «искусственный спутник Земли». Однако, если мы их сформулируем так, что возьмем в качестве рода множество никак не охарактеризованных предметов («нечто») и все остальные характеристики, по которым выделяем соответствующие объекты мысли, отнесем к видовым отличиям, то понятия оказываются сравнимыми. Таким образом, существенно обращать внимание на строение (формулировку) понятия.

При указанном выше способе сравнения содержаний понятий по информативности на основе отношения логического следования предполагается, что понятия имеют общий род, а сравниваются части содержаний, заключенные в видовых отличиях. Приведение подлежащих сравнению понятий к общему роду так же необходимо, как приведение сравниваемых дробей к общему знаменателю, и только при осуществлении такого приведения они становятся сравнимыми. Из данных разъяснений напрашивается мысль, что все понятия сравнимы, поскольку они могут быть всегда приведены к общему роду. Однако в определении сравнимости мы имеем в виду не возможность, а фактическое положение дел. И это существенно, поскольку понятие, полученное из какого-либо понятия изменением его рода, представляет собой уже иное понятие, чем исходное.

И. Среди несравнимых понятий не существует уже никаких отношений. В множестве пар сравнимых понятий выделяются с о в м е с т и м ы е и н е с о в м е с т и м ы е. Понятия совместимы, если признаки, составляющие содержание этих понятий, могут принадлежать одним и тем же предметам, их объемы имеют какие-то общие элементы. В противном случае понятия несовместимы. Например, совместимыми являются понятия: «активист» и «отличник», «философ- материалист» и «философ-метафизик», «философ-идеалист» и «философ-диалектик» и т. п. Здесь, как и в дальнейших примерах, подразумевается, что понятия сформулированы так, что они имеют общий род. Для первой пары понятий общим родом может быть класс людей или класс учащихся, для остальных — класс людей.

Необходимым и достаточным условием логической несовместимости понятий хА(х) и хВ(х) является пустота пересечения их объемов: WxA (x) n WxB (x) = 0. Для содержаний понятий в этом случае имеем Г, А[х) *= -. В[х). При этом, в случае логической несовместимости понятий, Г пусто (значит, может быть любым). При фактической несовместимости Г — некоторое непустое множество высказываний, относящихся к дескриптивным терминам в А(х) и В(х) (и любое его расширение).

В силу того, что Г есть множество высказываний (замкнутых формул), логическая несовместимость указанных понятий означает логическую истинность выражений Ух (А{х) гэ -, В{х)) и Ух (-. А{х) v -, В(х)) (логическая истинность формул означает истинность лишь в силу логических форм, независимых от значений дескриптивных терминов в них).

При фактической несовместимости эти выражения истинны в силу значений, имеющихся в А(х) и В{х) дескриптивных терминов.

Для совместимых понятий имеем: WxA (x) n WxB (x) *0 и истинное высказывание Зх (А{х) 8* B (x)). При этом для логической совместимости это высказывание истинно лишь в силу своей логической формы (то есть истинно независимо от значений дескриптивных терминов в составе форм А(х) и В{х)). Фактическая совместимость означает истинность указанных высказываний в силу данных значений дескриптивных терминов в А{х) и В(х) и, значит, с учетом некоторого множества знаний Г относительно этих терминов.

Несовместимые понятия: «студент — отличник» и «неуспевающий студент», «интернационалист» и «националист», «кристаллическое вещество» и «вещество, не имеющее определенной температуры плавления».

Ясно, что для решения вопроса о совместимости или несовместимости понятий нужно иметь сами понятия, а не слова, которые служат их сокращениями. Так, если молекулой называется наименьшая частица вещества, обладающая его химическими свойствами, то совместимыми, очевидно, являются понятия «молекула» и «атом», поскольку имеются так называемые одноатомные молекулы (например, молекулы инертных (благородных) газов).

Кстати, автор статьи «Молекула» в БСЭ (изд. 3-е), сформулировав указанное в начале определение ее, вместе с тем замечает, что «одноатомные молекулы по сути дела являются атомами вещества и поэтому (? — Д., В.), строго говоря, не могут быть отнесены к молекулам». Автор здесь противоречит сам себе. Согласно его определению молекулы, одноатомная молекула является молекулой в строгом смысле слова.

Виды совместимости

В множестве пар совместимых понятий различаются три вида: 1) равнозначные понятия; 2) понятия, находящиеся в отношении логического подчинения; 3) перекрещивающиеся понятия. Равнозначными называются понятия, объемы которых совпадают и только содержания различны. Таким образом, эти понятия выделяют один и тот же класс предметов, но по разным совокупностям признаков. Например, «равносторонний треугольник» и «равноугольный треугольник» (в Эвклидовой геометрии); «тело, на которое не действуют никакие силы, или равнодействующая всех сил равна нулю» и «тело, которое находится в состоянии покоя или равномерного прямолинейного движения», «студент, для которого не существует таких вопросов (данного) курса, на которые он не может ответить» и «студент, который может ответить на все вопросы (данного) курса».

Для содержания равнозначных понятий хА{х) и хВ(х) существует их эквивалентность А{х) = В{х), что означает Г, Л{х) t = В(х) и Г, В(х) 1= А(х). Если эти соотношения имеются при пустом Г — понятия логически равнозначны; если же только при некотором непустом Г (и, естественно, при всех возможных расширениях его в этом случае), то они оказываются фактически равнозначными (относительно этого Г).

Понятия в приведенных выше двух первых примерах фактически равнозначны (относительно множества аксиом геометрии и относительно множества утверждений физики), а в последнем имеем логическую равнозначность понятий, что очевидно в силу логических форм этих понятий х-,3у ->Р(х, у) и х Уу Р(х, у).

Относительно множества утверждений арифметики равнозначны «целое положительное число, отличное от 1 и не имеющее никаких делителей кроме себя и 1» и «целое положительное число; имеющее ровно два различных делителя» (в том и другом понятии выделяется класс простых чисел).

Понятия находятся в отношении логического подчинения, если объем одного из них составляет правильную часть объема другого (а содержания — в соответствии с законом обратного отношения - находятся в обратном отношении).

Понятие с более широким объемом называется подчиняющим, а другое — подчиненным. Примеры: «четырехугольник» и «прямоугольный четырехугольник», «философ» и «философ-материалист», «международные отношения» и «международные экономические отношения», «химически простое вещество» и «металл», «учащийся вуза» и «студент» («учащийся вуза или среднего специального учебного заведения»).

Для понятий хА{х) и хВ(х), находящихся в отношении логического подчинения, имеем: WxB { x) < zWxA (x) и Г, В(х) 1= А{х), но Г, А{х) * В[х). В случае пустого Г существует родовидовое отношение логического характера, при непустом Г — родовидовое отношение фактического характера (относительно Г). Таковы отношения понятий во всех указанных примерах, кроме последнего.

Отношение логического подчинения иначе характеризуют как родовидовое, называя понятие, объем которого включает объем другого в качестве своей правильной части, родовым по отношению к этому второму, а второе — видовым по отношению к первому. Класс предметов, составляющих объем родового понятия, называют родом для класса предметов, мыслимых во втором понятии, а этот второй класс, наоборот, видом предметов данного рода.

Перекрещивающимися называют такие понятия, в объемах которых имеются общие элементы, однако в составе каждого из них содержатся такие предметы, которые не являются элементами другого. Например, «участник движения за ядерное разоружение» и «предприниматель», «поэт» и «драматург», «студент» и «спортсмен» и т. п. Для перекрещивающихся понятий хА{х) и хВ(х) верно утверждение Зх[А(х) & В{х)) с учетом некоторого Г - в случае фактического перекрещивания или без учета Г — логическое отношение перекрещивания.

Виды несовместимости

Среди несовместимых понятий выделяются пары противоречащих, противоположных и соподчиненных понятий.

Противоречащими являются понятия вида хА{х)

и хВ(х), где А{х) = -1 В[х) и где В(х) в свою очередь неэквивалентно отрицанию некоторой формулы С{х), то есть такие, в одном из которых мыслятся предметы, лишенные каких-либо свойств, составляющих видовое отличие предметов, мыслимых в другом.

Эквивалентность А{х) - -, В{х) может быть фактической или логической. В общем случае наличие ее означает Г, А(х) n -, В{х) и Г, -л В[х) 1= А(х). При пустом Г эти понятия логически противоречивы: при наличии же этих отношений только при некотором непустом Г имеем отношение фактического противоречия (относительно данного Г). Для логически противоречивых понятий хА(х) и хВ{х) логически истинны высказывания V * (А{х) vB { x)) и V * (-, А(х) v -, В(х)). При фактической противоречивости этих понятий данные высказывания истинны в силу значений дескриптивных терминов в составе Л&> и В[х).

Примеры противоречащих понятий: «город, являющийся столичным» и «город, не являющийся столичным», «слово, изменяющееся по числам и падежам» и «слово, не изменяющееся по числам или не изменяющееся по падежам», «тело (материальное), находящееся в покое или в состоянии равномерного прямолинейного движения» и «тело, которое не находится в покое и не находится в состоянии равномерного прямолинейного движения».

Фактически противоречащими являются понятия «равносторонний прямоугольный четырехугольник» и «четырехугольник, у которого диагонали в точке пересечения не делятся пополам», «ромб» и «неравносторонний четырехугольник».

К числу противоположных понятий относят, например, такие, как «человек высокого роста» и «человек низкого роста», «черное» и «белое», «человек высоконравственный» и «безнравственный человек». Обычно мы более или менее удачно применяем термин «противоположности» при интуитивном его употреблении. Определение же его смысла является трудной проблемой. Как правило, в этом отношении находятся понятия, которые отражают крайние степени какой-либо интенсивности. Более конкретно речь идет о понятиях, объемы которых составляют два крайних вида в множестве видов, которые выделены и расположены по степени изменения какого-нибудь признака. Так, например, объем понятия «ахроматический цвет» можно разделить по степени яркости на «белый», «светло-серый», «серый», «темно-серый», «черный». Таким образом, «белый» и «черный» здесь оказываются противоположностями. По-видимому, в любом случае, говоря о противоположных понятиях, мы подразумеваем возможность какого-либо упорядочивания видов предметов, входящих в его объем.

Среди философских систем различают материализм (исходное положение которого состоит в том, что материя первична, а сознание вторично, то есть является продуктом развития материи), дуализм (согласно представлениям которого материя и сознание существуют независимо друг от друга), идеализм (считающий, что сознание — идея, духовное вообще — первично, материя — вторична). Таким образом, идеализм есть противоположность материализма.

Наконец, два несовместимых понятия, которые не являются ни противоречащими, ни противоположными, называются с о п о д ч и н е н н ы м и. Например, «прямолинейное движение» и «криволинейное движение», «животное» и «растение» и т. п.

Приняты следующие графические изображения отношений между объемами совместимых и несовместимых понятий.

1. Отношение совместимости:

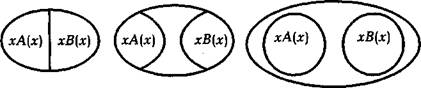
2. Отношение несовместимости:

Противоречие Противо- Соподчинение положность

Каждой из указанных схем может быть сопоставлена совокупность некоторых высказываний. Так, схема логического подчинения указывает на истинность высказывания: «Всякий предмет из области х, обладающий характеристикой В, есть предмет, имеющий характеристику А и только некоторые предметы, имеющие характеристику А суть предметы, обладающие характеристикой В», и «Всякий предмет из области х есть А или В». Читателю предлагается самому проанализировать с указанной точки зрения все другие схемы.

Таким образом, связывая схемы с определенным высказыванием, мы имеем некоторый способ проверки того, правильно ли определено отношение между теми или иными понятиями. Например, изобразив отношение между понятиями

«слово» — А и «существительное» — В схемой {&)), мы

принимаем за истинные утверждения: «всякое существительное есть слово» и «только некоторые слова суть существительные». Если же А есть «слово», а В — «корень слова», то при таком же изображении отношения между этими понятиями нужно было бы признать, что «Всякий корень слова есть слово». Но при том употреблении термина «слово», которое принято в лингвистике, это, очевидно, неверно.

Дело в том, что корень слова — это не вид слова, а его часть. Между понятиями нет родовидового отношения.

Для успешного решения вопросов об отношении тех или иных понятий, естественно, нужно точное знание содержания, а тем самым и объема понятий. Как, например, решить вопрос об отношении между понятиями «дерево, имеющее лиственную крону» и «дерево, имеющее хвойную крону», не имея понятия «листья»? Если хвоя — вид листьев, тогда второе является подчиненным первому. Однако часто знание отношений между понятиями, а тем более процесс их установления способствует уточнению, углублению содержаний употребляемых понятий. И, конечно, овладение процедурой выяснения отношений между понятиями способствует развитию аналитических способностей мышления.

• Упражнения

1. Какие из следующих отношений между понятиями яв ляются отношениями «рода и вида», а какие отношениями «часть и целое»:

а) школа, средняя школа; б) четырехугольник и сторона четырехугольника; в) натуральный ряд чисел, геометрическая прогрессия; г) ромб, квадрат; д) Китай, Азия; е) множество натуральных чисел, множество четных натуральных чисел; ж) часть Китая, часть Азии; з) кислота, химически сложное вещество?

2. Изобразите посредством круговых схем отношения между понятиями:

• а) естественный спутник какого-нибудь небесного тела, спутник Земли, небесное тело, спутник Марса, спутник ка кого-нибудь небесного тела, искусственный спутник какого- нибудь небесного тела;
• б) мужество, упорство, упрямство;
• в) дед, сын, брат, мужчина, отец, внук, дядя, племянник;
• г) уравнение, уравнение с целочисленным решением, уравнение, не имеющее решения, уравнение с решением в рациональных числах;
• д) окружность, геометрическое место точек, равноудален ных от одной точки, полусфера, дуга окружности, сфера;
• е) корень квадратный из 4, четное число, нечетное число, корень квадратный из 9, число, деление на которое дает то же число; число, на которое не делится никакое число; ко рень квадратный из 1;
• ж) слово, изменяющееся по лицам; слово, изменяющееся по падежам, спрягаемое слово, глагол, прилагательное, наре чие, существительное.

3. Укажите какие-нибудь понятия, отношения между которыми удовлетворяют следующим схемам:

4. Какие отношения между понятиями «объективный человек», «честный человек» и «справедливый человек» имеются в виду в утверждениях (изобразите эти отношения посредством круговой схемы):

• а) ни один необъективный человек не является справедливым;
• б) некоторые честные люди справедливы и наоборот;
• в) ни один честньш не является необъективным 1?

5. Опрос 100 студентов дал следующие результаты о количестве изучающих различные иностранные языки: английский — 28, немецкий — 30, французский — 42, английский и немецкий — 8, английский и французский — 10, немецкий и французский — 5, все три языка — 3.

• а) Сколько студентов не изучает ни одного языка?
• б) Сколько студентов изучает только французский язык?
• в) Сколько студентов изучает только немецкий язык?
• г) Сколько студентов изучает только английский язык?
• д) Сколько студентов изучает немецкий язык в том и только в том случае, если они изучают французский язык?
• е) Сколько студентов изучает немецкий язык в том и только в том случае, если они не изучают английский язык?

(Ук а з а н и е. Нарисуйте схему в виде трех кругов, обозначающих студентов, изучающих соответственно английский, французский и немецкий языки. В каждую из полученных областей впишите цифры, исходя из условия задачи.)

i При затруднении обратитесь к разделу «Непосредственные выводы из категорических суждений» § 36.

 

 

Поделиться:

Воспользуйтесь поиском по сайту: