Интегрирование методом замены

Производные функции

Производной функции в точке называется предел отношения приращения функции в этой точке к приращению аргумента при , если этот предел существует:

. (1.1)

Функция , имеющая производную в каждой точке некоторого промежутка, называется дифференцируемой в этом промежутке.

Для производной функции употребляются следующие обозначения: , , , .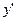

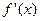Нахождение производной называется дифференцированием.

Правила дифференцирования:

1. ;

2. ;

3. ;

4. .

 

 

Таблица производных

Таблица основных производных:

Таблица 1

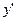
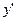
С-постоянная
				-
				-

 

 

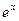
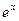
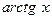
Производная сложной функции.

Производной второго порядка функции называется производная от её производной, т.е.

20. . (1.2)

Производную от второй производной называют производной третьего порядка.

В общем случае производной n-го порядка называется производная от производной (n-1)-го порядка: .

Пусть и , тогда – сложная функция с промежуточным аргументом u и независимым аргументом x.

Для нахождения производной сложной функции надо производную данной функции по промежуточному аргументу умножить на производную промежуточного аргумента по независимому аргументу:

21. 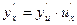. (1.3)

1.Найдём производную функции , используя формулу (1.3). Данная функция не является элементарной. Полагая , получим . Находим .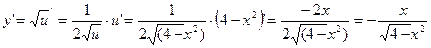

 

Производная в точке. Для вычисления производной функции в точке нужно в выражение производной вместо переменной подставить значение . В итоге должно получиться число.

 

 

4. Производная высшего порядка.

Производной n -го порядка (n -ой производной) от функции f (x) (n >1) называется производная первого порядка от производной (n -1) порядка функции f (x) при условии, что она существует.

f (n)(x) = (f (n -1)(x)) ',

 

5. Частные производные:

Частные производные

Каждая частная производная (по x и по y) функции двух переменных представляет собой обыкновенную производную функции одной переменной при фиксированном значении другой переменной:

(где y = const),

 

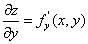
(где x = const).

 

Пример 1. Найти частные производные функции

Решение. Имеем

( y фиксировано);

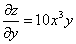
( x фиксировано).

 

Дифференциал функции

Дифференциалом функции (или дифференциалом первого порядка) называется произведение производной этой функции 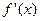на произвольное приращение аргумента :

. (3.1)

Дифференциал аргумента равен приращению аргумента: . Поэтому дифференциал функции равен произведению её производной на дифференциал аргумента:

(3.2.)

Дифференциалом второго порядка называется дифференциал от дифференциала первого порядка:

, (3.3)

т. е. дифференциал второго порядка функции равен произведению второй производной этой функции на квадрат дифференциала аргумента.

Пример

1. Найдите дифференциалы первого порядка.

а) ;

;

б) ;

.

2. Найдите дифференциалы второго порядка.

а) ;

;

;

;

б)

;

;

Интеграл функции

Тема 4.Интегрирование функции.

Функция называется первообразной для функции в промежутке , если в любой точке этого промежутка ее производная равна :

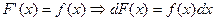, . (4.1)

Операция отыскания первообразной функции по заданной ее производной или по дифференциалу называется интегрированием.

Совокупность первообразных для функции или для дифференциала называется неопределённым интегралом и обозначается символом . Таким образом,

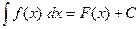, (4.2)

если .

Здесь - подынтегральная функция; - подынтегральное выражение; С – произвольная постоянная.

Основные свойства неопределённого интеграла.

1. ;

2. ;

3. ;

4. ;

5. .

 

Таблица интегралов

1. ;

2. ;

3. ;

4. ;

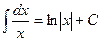5. ;

6. ;

7. ;

8. ;

9. ;

10. ;

11. ;

12. ;

13. ;

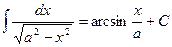14. .

Интегрирование методом замены

Интегрирование методом замены переменной (способ подстановки). Сущность интегрирования способом подстановки заключается в преобразовании интеграла в интеграл 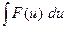, который легко вычисляется по какой-либо из основных формул интегрирования. Для нахождения интеграла заменяем переменную новой переменной с помощью подстановки 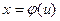. Дифференцируя это равенство, получим . Подставляя в подынтегральное выражение вместо и их значения, выраженные через и , имеем .

После того как интеграл относительно новой переменной будет найден, с помощью подстановки он приводится к переменной .

10. Интегрирование по частям:

Интегрирование по частям. Если , - дифференцируемые функции, то справедлива формула .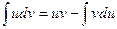

С помощью этой формулы вычисление интеграла 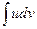сводится к вычислению интеграла 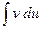, если последний окажется проще исходного

Методы интегрирования функции сводятся к указанию приемов, приводящих данный интеграл к табличному. Необходимо знать табличные интегралы и уметь их узнавать.

Для того чтобы проверить правильно ли найден интеграл, необходимо найти производную от получившейся функции и получить подынтегральное выражение.

При вычислении интегралов часто используется формула .

Пример 1.

.

Пример 2.

В этих примерах также можно использовать метод замены переменной.

Интегрирование по частям состоит в том, что подынтегральное выражение заданного интеграла представляется каким-либо образом в виде произведения двух сомножителей и , затем, после нахождения и , используется формула интегрирования по частям.

Типы интегралов, которые удобно вычислять методом интегрирования по частям:

1. Интегралы вида , , , где – многочлен, k – число. Удобно положить , а за обозначить все остальные сомножители.

2. Интегралы вида , , , , 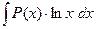. Удобно положить , а за обозначить остальные сомножители.

3. Интегралы вида , , где а и b – числа. За можно принять функцию .

При нахождении интегралов (а-г) используется непосредственное интегрирование. Интегралы (б-г) также можно найти методом замены переменной. Интеграл (е) находится интегрированием по частям.

 

 

Поделиться:

Воспользуйтесь поиском по сайту: