о статической устойчивости асинхронных двигателей, входящих в состав комплексной нагрузки

Пример выполнения контрольной работы по дисциплине «Электромеханические переходные процессы»

Некоторые теоретические сведения

о статической устойчивости асинхронных двигателей, входящих в состав комплексной нагрузки

    Под статической устойчивостью асинхронного двигателя понимается его способность возвращаться к установившемуся режиму после малых возмущений, которые могут возникать в результате изменений режимов работы как самой электрической системы так и асинхронного двигателя, например отключения части питающих линий, при оперативных переключениях и в результате изменений режимов.

    Если узлы нагрузки по суммарной потребляемой мощности соизмеримы с мощностью питающей системы или электрически удалены от источников электрической энергии, то режим их работы при малых возмущениях может оказаться неустойчивым.

    Рассмотрим условия устойчивости асинхронного двигателя применительно к схеме, представленной на рис. 1. В узел нагрузки входит эквивалентный асинхронный двигатель и осветительная нагрузка. Узел нагрузки питается от генератора (станции) G через трансформатор Т 1, линию электропередачи W, трансформатор Т 2.

 

 

 

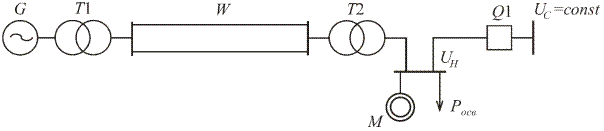
Рис. 1. Расчетная схема системы электроснабжения узла нагрузки

 

В исходном режиме питание узла нагрузки полностью обеспечивается удаленной станцией G, кроме того, шины нагрузки имеют связь с шинами системы бесконечной мощности. В исходном нормальном режиме при номинальном напряжении на шинах нагрузки =1 и номинальном скольжении  через выключатель  переток активной и реактивной мощности равен нулю. Наличие связи с системой обеспечивает во всех режимах неизменное напряжение на шинах нагрузки . Анализ устойчивости асинхронного двигателя выполняется для двух случаев.

1. Выключатель  включен (рис. 1). Наличие связи с системой бесконечной мощности обеспечивает во всех режимах, в том числе и отличных от исходного, неизменное напряжение на шинах нагрузки .

    2. Выключатель  отключен (рис. 1). Узел нагрузки отключен от системы бесконечной мощности. Нагрузка питается от генераторов удаленной станции. Напряжение на шинах нагрузки в этих условиях не остается постоянным, а изменяется при изменениях режима работы нагрузки .

    Схема замещения исследуемой системы приведена на рис. 2.

        

Рис. 2. Схема замещения исследуемой системы

    При составлении схемы замещения двигателя не учитываются потери активной мощности в стали, а также в меди статора, индуктивное сопротивление цепи намагничивающего тока  отнесено непосредственно к выводам двигателя. Индуктивное сопротивление  представляет сумму индуктивных сопротивлений рассеяния статора и ротора, – активное сопротивление ротора приведенное к статору, 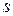– скольжение. При составлении схемы замещения внешней сети не учитываются активные сопротивления линий и трансформаторов, зарядные мощности линий. Осветительная нагрузка представлена активным сопротивлением .

    Выполним анализ устойчивости асинхронного двигателя при условии, что мощность механизма, приводимого во вращение двигателем, не зависит от его скольжения, т. е. 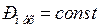и при номинальном напряжении равна номинальной мощности двигателя 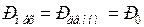, т. е. коэффициент загрузки принят равным 1.

1. Рассмотрим условия устойчивости асинхронного двигателя вначале при включенном положении выключателя Q 1. При включенном положении выключателя  нагрузка питается от шин мощной системы. Наличие этой связи обеспечивает во всех режимах, отличных от исходного, неизменное напряжение на шинах нагрузки .

Рассмотрим процесс нарушения статической устойчивости асинхронного двигателя.

В соответствии со схемой замещения двигателя (рис. 2) потребляемая им активная мощность   в функции скольжения может быть определена по известной формуле:

.                          (1)

В выражении (3.1) скольжение двигателя определяется по выражению 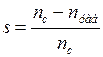, где ,  – синхронная и рабочая частоты вращения ротора двигателя. Очевидно, при , а если то .

Кроме того, формула (1) показывает, что при постоянных параметрах схемы замещения двигателя и напряжении на его зажимах , активная мощность  зависят только от скольжения  и , т. е. величина  связана с напряжением квадратичной зависимостью.

На рис. 3.3 представлены: зависимость мощности механизма, не зависящая от скольжения , и семейство характеристик  при изменении скольжений от  до 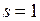 при различных постоянных напряжениях на зажимах двигателя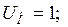 , где  некоторое критическое напряжение.

Амплитудное значение  каждой из зависимостей  имеет место при скольжении, называемом критическим .

Пересечение каждой из кривых  и  (точки 1, 2, К 1 рис. 3) соответствуют равновесным режимам работы асинхронного двигателя.

     

 

Рис. 3. Характеристики мощности двигателя

при различных значениях напряжения

 

При напряжении на зажимах двигателя  имеет место нормальный устойчивый установившийся режим в точке 1 со скольжением , близком или равном номинальному и соотношением мощностей .

При понижении напряжения на зажимах двигателя до величины, например, 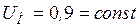 на валу двигателя возникает избыток мощности , соответствующий отрезку , двигатель тормозится, скольжение возрастает и в точке 2 при скольжении 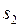 устанавливается новый стационарный установившийся режим, при этом так же максимальная мощность двигателя больше мощности механизма . При  на зажимах двигателя и скольжении  максимальная мощность двигателя равна мощности механизма  (рабочая точка К 1), двигатель имеет критическое состояние равновесия, он находится на границе устойчивости, а при  максимальная мощность двигателя становится меньше мощности механизма , двигатель теряет устойчивость, выбегает, «опрокидывается» и при этом скольжение его растет, становится больше критического .

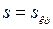Таким образом, рабочие точки 1, 2 и любая другая точка на восходящей части зависимости  являются точками устойчивых режимов работы и критерий устойчивых режимов можно сформулировать как . Рабочая точка К 1 при  и  – предельный режим работы двигателя, для которого . Из рис. 3 видно, что диапазон скольжений, при которых обеспечивается устойчивая работа двигателя, находится в интервале от  до критического . Величину  можно определить по каталожным параметрам двигателя, а можно и по схеме замещения. Если взять первую производную выражения (1) и приравнять результат выражения производной при 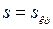  к нулю (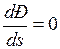) получим

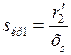.                                              (2)

    Подставив  в уравнение (1), получаем наибольшее значение активной мощности двигателя, соответствующее «опрокидывающему моменту»:

.                                         (3)

    «Опрокидывающий момент», таким образом, зависит от напряжения на зажимах двигателя. С уменьшением напряжения значение опрокидывающего момента, как и  в целом, быстро падает по квадратичной зависимости. Наименьшим напряжением, при котором еще возможна работа асинхронного двигателя, является критическое напряжение. При этом напряжении имеется лишь одна рабочая точка(т. К 1), в которой мощность двигателя равна мощности механизма. При напряжении, равном критическому , максимальная мощность двигателя оказывается равной мощности механизма.

    Из выражения (3) с учетом, что  при  получаем выражение для критического напряжения:

.                            (4)

Величина критического напряжения может служить показателем степени устойчивости двигателя. Чем выше значение критического напряжения, тем менее устойчив двигатель.

      Количественно запас устойчивости асинхронного двигателя оценивается по коэффициентам запаса 

– по напряжению:                                                                                 

,                                (5)

– по мощности:     

                        ,                                        (6)

 

– по скольжению:              

                        ,                               (7)

    Обычно двигатели, подключаемые к шинам напряжения, не зависящего от их режима, работают с весьма большим запасом устойчивости. Именно такая ситуация соответствует включенному положению выключателя .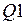

    2. При отключенном положении выключателя 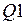 двигатель оказывается подключенным через внешнее сопротивление  от удаленного источника ЭДС 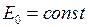 (см. рис. 2).

    Напряжение на выводах двигателя в этих условиях не остается постоянным, а падает с увеличением скольжения в связи с потерями напряжения во внешнем индуктивном сопротивлении. Это обстоятельство в существенной степени влияет на условия устойчивости двигателя. Если в схеме замещения двигателя опустить индуктивное сопротивление цепи намагничивания, то при постоянстве , приложенной за внешним индуктивным сопротивлением , значение опрокидывающего момента может быть найдено по аналогии с (3.3):

,                                       (8)

и критическое скольжение - по аналогии с (2):

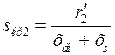.                                     (9)

    Изменение характеристики мощности двигателя под влиянием внешнего сопротивления показано на рис. 4. Из рис. 4 видно, что опрокидывающий момент  и критическое скольжение  заметно уменьшаются. Быстрое понижение характеристики с ростом скольжения, начиная с , при неизменной ЭДС 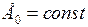, объясняется нарастающей потерей напряжения во внешнем индуктивном сопротивлении. Запас устойчивости, определяемый по выражениям (5) – (7), в этом случае оказывается меньше, чем в случае питания двигателя от шин неизменного напряжения.

Рис.4. Сравнение условий устойчивости асинхронного двигателя

при наличии внешнего сопротивления и при его отсутствии

 

В соответствии с выражением (8) при уменьшении ЭДС мощность двигателя падает по квадратичной зависимости (рис. 4). При снижении ЭДС до критической максимальная мощность двигателя становится равной мощности механизма. В этом случае при критической ЭДС существует одна рабочая точка – точка К 2. При дальнейшем снижении ЭДС работа двигателя будет невозможна, он остановится. Величина  определяется по выражению:

.                             (10)

     Запас устойчивости по ЭДС может быть определен в соответствии с выражением:

 %.                          (11)

 

Рассмотрим условия обеспечения статической устойчивости узла нагрузки, состоящего из однотипных асинхронных двигателей. Схема электроснабжения представлена на рис. 5. Электроснабжение узла нагрузки осуществляется по линии электропередачи напряжением 110 кВ от источника питания Е = const.

Рис.5. Расчетная схема системы электроснабжения

 

Узел нагрузки представлен группой однотипных асинхронных двигателей, равномерно распределенных по секциям шин 6 кВ. Количество двигателей, подключенных к одной секции, равно n, общее число двигателей равно N =2 n.

Номинальная активная мощность, потребляемая эквивалентным асинхронным двигателем, равна:

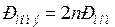                                        (12)

 

где  – номинальная активная мощность одиночного двигателя.

Реактивная мощность, потребляемая асинхронным двигателем, определяется по выражению:

                         (13)

или по выражению:

                                (14)

где 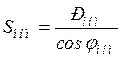 – полная номинальная мощность асинхронного двигателя.

Для эквивалентного асинхронного двигателя полная и реактивная мощности, соответственно, будут равны:

                                 (15)

                                 (16)

Поскольку в узел нагрузки входят однотипные двигатели, то такие параметры эквивалентного АД, как коэффициент загрузки , кратность максимального момента , коэффициент мощности , номинальное скольжение  будут равны аналогичным параметрам одиночного двигателя: , , , .

Исследование устойчивости обычно выполняется в относительных единицах, приведенных к базисным условиям. При расчетах электромеханических переходных процессов, связанных с устойчивостью нагрузки, за базисную мощность удобно принимать суммарную полную мощность двигательной нагрузки , а за базисное напряжение – номинальное напряжение двигателей .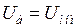

Параметры схемы замещения эквивалентного асинхронного двигателя в относительных единицах, приведенных к этим базисным условиям, могут быть определены с помощью следующих выражений:

 

- индуктивное сопротивление эквивалентного двигателя:

,                                         (17)

- индуктивное сопротивление цепи намагничивания:

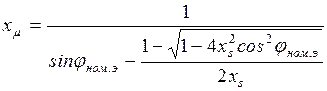                     (18)

 

- активное сопротивление ротора:

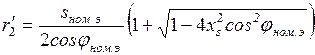                        (19)

 

где                  

 

Пример 1.  Выполнить анализ статической устойчивости  узла нагрузки, состоящего из двенадцати однотипных асинхронных двигателей марки А-13-59-4, к каждой секции шин подключено по 6 двигателей (n =6) при условии, что питание осуществляется через один трансформатор и одну линию (Т1 отключен, секционный выключатель включен) (рис. 5).

Паспортные данные двигателей приведены в табл. 1. Узел нагрузки подключен к источнику питания напряжением 110 кВ через двухцепную воздушную линию электропередачи АС-150 длиной 47 км и трансформаторы ТРДН – 25000/110/6 (рис. 5). Паспортные данные трансформатора приведены в табл. 2, погонные параметры линии – в табл. 3.

Таблица 1

Параметры двигателей (U _ном.дв = 6 кВ)

Тип двигателей	Рном, МВт	cos φ	η, %	пном, об/мин	пС, об/мин	b Н, о.е.	МП, о.е.	КП, о.е.	J, кг∙м2	пдв, шт	k З, о.е.
А-13-59-4	1	0,91	94	1485	1500	2,5	1,2	6,2	62,5	6	0,9

 

Таблица 2

           Параметры трансформаторов

Тип трансформаторов	S ном, МВА	U ном.В, кВ	U ном.Н, кВ	UK, %
ТДН-25000/110/6	25	115	6,3	10,5

 

Таблица 3

           Параметры ЛЭП

Марка провода	L, км	х 0, Ом/км
АС-150	47	0,416

 

1.1. Составить схему замещения заданной системы электроснабжения и рассчитать ее параметры. При расчете параметров сети внешнего электроснабжения допускается не учитывать:

    - потери холостого хода трансформаторов и их активные сопротивления;

    - активные сопротивления и емкостные проводимости воздушных линий электропередачи.

При составлении схемы замещения узла нагрузки группа однотипных двигателей представляется эквивалентным двигателем и эквивалентной схемой замещения.

    Механический момент сопротивления механизма принимается независимым от скольжения и равным .

    1.2. Построить характеристику мощности эквивалентного двигателя , определить параметры предельных режимов , , , определить коэффициенты запаса статической устойчивости эквивалентного асинхронного двигателя , , .

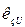    1.3. Рассмотреть мероприятия по обеспечению статической устойчивости в случае если необходимый запас не обеспечивается.

 

Решение.

1. Определим параметры эквивалентного АД.

 МВт,

 МВ∙А,

; ; ,

где , .

2. Выберем базисные условия. В качестве базисных условий примем 

 МВ∙А,  кВ.

Базисное напряжение для ступени 110 кВ будет равно:

                                       (20)

где – номинальные напряжения обмоток высшего и низшего напряжений трансформатора, соответственно.

 кВ.

3. Составим схему замещения исследуемой системы электроснабжения и определим ее параметры.

Схема замещения рассматриваемой системы электроснабжения представлена на рис. 6­­, В схеме замещения учтены только индуктивные сопротивления линии и трансформатора. Для упрощения анализа ветвь намагничивания АД перенесена в узел подключения ЭДС.

 

 

 

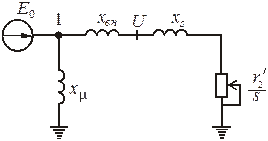
Рис. 6. Преобразованная схема замещения сети после вынесения ветви

намагничивания к точке приложения ЭДС

 

Параметры схемы замещения  эквивалентного асинхронного двигателя  определяются по выражениям (17, 18,19):

,

,

,

где .

Индуктивное сопротивление трансформатора определяется по выражению:

                                (21)

.

Индуктивное сопротивление одной цепи ВЛ определяется по выражению:

,                                          (22)

где  – базисное сопротивление на ступени 110 кВ.

 Ом, .

Внешнее сопротивление равно сумме сопротивлений линии и трансформатора:

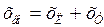,                                      (23)

.

Анализ статической устойчивости выполняется при условии, что мощность механизма не зависит от скольжения: .

Мощность механизма определяется с учетом коэффициента загрузки по выражению:

,                                        (24)

.

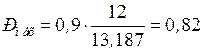В исходном режиме активная мощность двигателя равна мощности механизма: .

Для рассматриваемой задачи .

Реактивную мощность эквивалентного двигателя можно упрощенно определить по выражению (3):

;

.

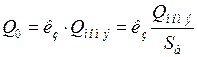В исходном режиме напряжение на шинах двигателя равно номинальному, а в относительных единицах:

,                                          (25)

.

ЭДС эквивалентного источника, обеспечивающая исходный режим работы двигателя с параметрами , ,                                                     определяется по выражению:

,                      (26)

.

Для определения рабочего скольжения эквивалентного двигателя               при  и  необходимо решить уравнение:

,                                     (27)

где , .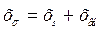

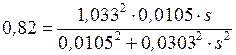 .                         (28)

Уравнение (28) является квадратным относительно s, решая его получаем два корня , .

Критическое скольжение согласно (9) равно:

.

Устойчивому режиму работы двигателя () соответствует скольжение , оно и является рабочим (), а неустойчивому () – скольжение 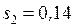 (0,14>0,0347).                                              

Максимальная мощность , т.е. мощность развиваемая двигателем при скольжении  равна, согласно (8):

.

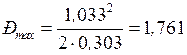Критическая ЭДС, при которой имеет место только одна рабочая точка  при  согласно (10) равна:

.

Критическое напряжение, т.е. напряжение на шинах двигателя, соответствующее этой ЭДС, равно при 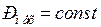 с учетом принятых допущений:

,                               (29)

.

Для построения характеристики мощности эквивалентного двигателя   рассчитаем значения активной мощности при различных значениях скольжения по выражению (27):

.

Результаты расчета приведены в табл. 4 и на рис. 7.

Таблица 4 

s, о.е.	0	=0,0086	=0,0347	0,14	0,2	0,3	0,5	0,7	1
P, о.е.	0	0,82	1,761	0,82	0,592	0,4	0,243	0,174	0,122

 

Коэффициенты запаса устойчивости согласно (5, 6, 7, 11) равны:

,

,

,

.

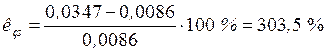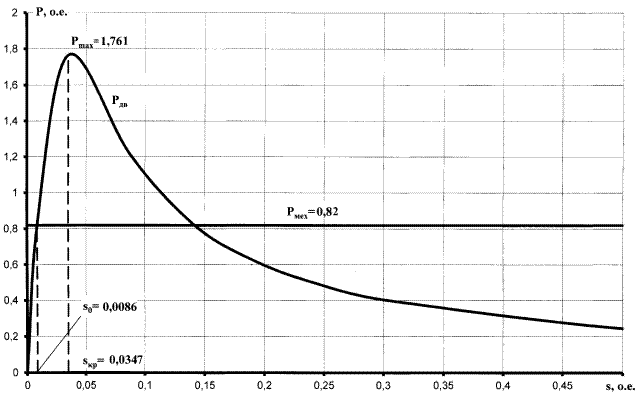
Рис. 7.

 

Вывод. Устойчивость нагрузки, состоящей из 12 АД типа при заданных условиях работы обеспечивается. Запас устойчивости эквивалентного двигателя достаточный. Следует отметить, что коэффициент запаса по напряжению больше нормативного, равного 15%.

Поделиться:

Воспользуйтесь поиском по сайту: