 |
Определение качественных показателей системы
|
|
|
|
Для этих целей используется прикладная программа Simulink и её подпрограмма Control System Toolbox – инструментарий систем управления – предназначенный для моделирования, анализа и проектирования непрерывных автоматических систем. Пакет реализует методы исследования динамических систем, в основу которых положены передаточные функции и графические модели. Основным вычислительным ядром рассматриваемого пакета является программа подраздела LTI (Lienear Time-Invariant System - программа разработки линейных инвариантных во времени систем управления (СУ), которые в отечественной литературе называются линейными стационарными СУ). Программа LTI позволяет анализировать качественные показатели системы с помощью отображения графиков.
Получены следующие графики с помощью программы LTI:
1.) реакция системы на единичную ступенчатую функцию – график 1;
2.) реакция системы на единичную функцию – график 2;
3.) амплитудно-частотная и фазово-частотная характеристика (АЧХ и ФЧХ) системы – график 3;
4.) абсолютная величина изменения АЧХ – график 4;
5.) корневой годограф Найквиста – график 5;
6.) годограф Николса – график 6;
7.) карта нолей и полюсов – график 7.
На графиках даны следующие характеристики:
1.) Setting Time – время переходного процесса;
2.) Rise Time – максимальная скорость;
3.) Steady State – точка достижения заданного значения выходного параметра;
4.) Stability Margins (Minimum only, All crossing) – запас устойчивости;
5.) Pole – корни характеристического уравнения;
6.) Damping – коэффициент демпфирования;
7.) Overshoot – коэффициент перерегулирования;
8.) Frequency – период собственных колебаний;
9.) Peak Response – пик изменяющейся характеристики.
График 1. Реакция системы на единичную ступенчатую функцию.
|
|
|
Из графика 1 видно, что при времени переходного процесса 11,3 секунды процесс входит последний раз в пятипроцентную зону, перерегулирования нет, в целом, график переходного процесса похож на плавный апериодический.
График 2. Реакция системы на единичную функцию (1 – система с отрицательными обратными связями, 2 – система без обратной связи в контуре положения).
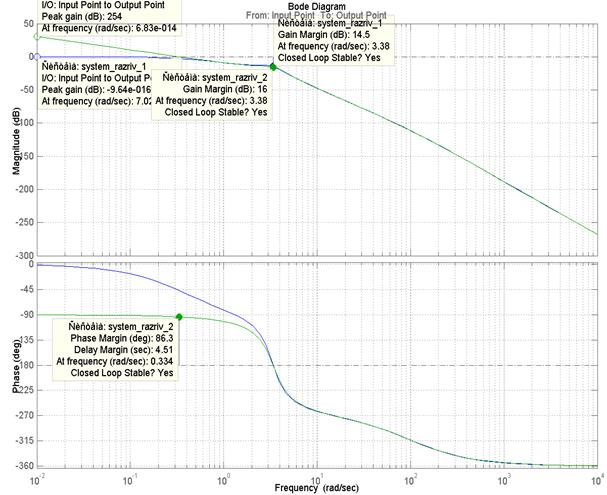
График 3. АЧХ и ФЧХ системы.
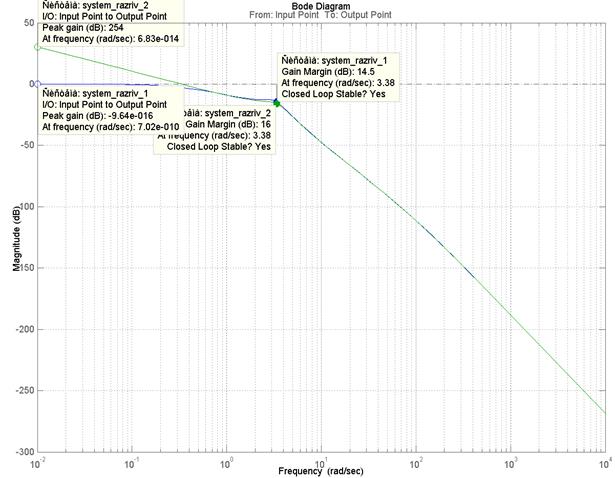График 4. Абсолютная величина изменения АЧХ.
График 5. Корневой годограф Найквиста.
График 6. Годограф Николса.
График 7. Карта нолей и полюсов.
На графике 7 представлена плоскость корней. График 7: можно определить устойчивость системы корневым методом. По графику s1=-100, s2=-0,351, s3=-0,891+3,2i, s4==-0,891+3,2i – это корни характеристического уравнения (приравниваем к нулю знаменатель суммарной передаточной функции). Все корни лежат в левой полуплоскости, следовательно, система устойчивая.
СИНТЕЗ СИСТЕМЫ
По техническому заданию необходимо, чтобы системы обладала следующим набором характеристик:
- коэффициент перерегулирования σн=16,3% и σ=6,3%,
- время переходного процесса tп=6c,
- время первого согласования t1=1,38c,
- статическая погрешность δС=±0,157рад.
Для достижения заданных в техническом задании качественных показателей системы в замкнутый контур системы устанавливается пропорционально-интегро-дифференциальный регулятор (ПИД-регулятор) между ДОС по скорости и колебательным звеном ТПМ. Для расчета коэффициентов ПИД-регулятора используется прикладная программа Simulink с пакетом подпрограммы Nonlinear Control Design (NCD) (проектирование нелинейных систем управления), который предназначен для параметрической оптимизации замкнутых систем. Он является специализированной программой для решения задач оптимизации значений параметров при наличии ограничений в форме неравенств и использующий в качестве алгоритма оптимизации последовательное квадратичное программирование. В данной курсовой работе этот пакет прикладной программы используется для оптимизации коэффициентов ПИД-регулятора.
|
|
|
Перевод значений перерегулирования в радианы. Составим пропорцию
, где
5 – установившееся значение в радианах,
16,3 – значение нижнего перерегулирования в процентах, откуда
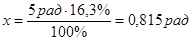
- нижнее перерегулирование.
Аналогично, для верхнего перерегулирования
- верхнее перерегулирование.
Расчёт в радианах пятипроцентной зоны:
В результате работы программы NCD получены следующие коэффициенты PID-регулятора при периоде квантования 0,05 секунды:
Kp=2,3153;
Ki=5,8446;
Kd=0,4191.
График переходного процесса системы с использованием PID-регулятора показан на рисунке 1 ниже.
Рисунок 1. Переходный процесс с использованием PID-регулятора.
В результате, время переходного процесса снизилось на 8,8 секунды до 2,5 секунд, при времени первого согласования 1,38 секунд выход составляет 4,15 радиан, что удовлетворяет техническому заданию.
ЗАКЛЮЧЕНИЕ
В работе спроектирован электрический привод подач металлорежущего станка с применением PID-регулятора, удовлетворяющий требованиям tп=6c, t1=1,38c, σ=6,3%, σн=16,3% и δС=±0,157рад. Коэффициенты PID-регулятора: Kp=2,3153, Ki=5,8446 и Kd=0,4191.
ПРИЛОЖЕНИЕ
|
|
|
12 |
