Линейная функция, её свойства и график.

Понятие числовой функции. Способы задания функции. Свойства функций.

 

Числовая функция — функция, которая действует из одного числового пространства (множества) в другое числовое пространство (множество).

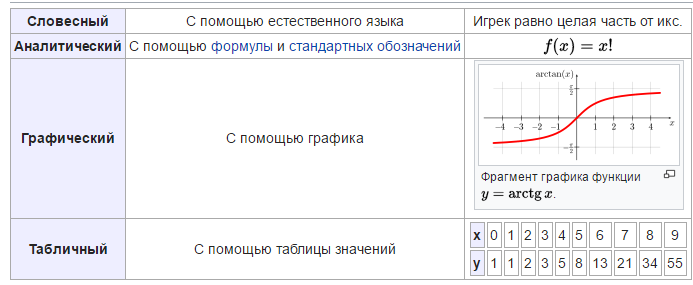
Три главных способа задания функции: аналитический, табличный и графический.

1. Аналитический.

Способ задания функции при помощи формулы называется аналитическим. Этот способ является основным в мат. анализе, но на практике не удобен.

2. Табличный способ задания функции.

Функцию можно задать с помощью таблицы, содержащей значения аргумента и соответствующие им значения функции.

3. Графический способ задания функции.

Функция у=f(х) называется заданной графически, если построен ее график. Такой способ задания функции дает возможность определять значения функции только приближенно, так как построение графика и нахождение на нем значений функции сопряжено с погрешностями.

Свойства функции, которые необходимо учитывать при построении её графика:

1)Область определения функции.

Область определения функции, то есть те значения, которые может принимать аргумент х функции F =y (x).

2) Промежутки возрастания и убывания функции.

Функция называется возрастающей на рассматриваемом промежутке, если большему значению аргумента соответствует большее значение функции у(х). Это означает, что если из рассматриваемого промежутка взяты два произвольных аргумента х₁ и х₂, причём х₁ > х₂, то у(х₁) > у(х₂).

Функция называется убывающей на рассматриваемом промежутке, если большему значению аргумента соответствует меньшее значение функции у(х). Это означает, что если из рассматриваемого промежутка взяты два произвольных аргумента х₁ и х₂, причём х₁ < х₂, то у(х₁) < у(х₂).

3) Нули функции.

Точки, в которых функция F = y (x) пересекает ось абсцисс (они получаются, если решить уравнение у(х) = 0) и называются нулями функции.

4)Чётность и нечётность функции.

Функция называется чётной, если для всех значений аргумента из области определения

у(-х) = у(х).

График чётной функции симметричен относительно оси ординат.

Функция называется нечётной, если для всех значений аргумента из области определения

у(-х) = -у(х).

График чётной функции симметричен относительно начала координат.

Многие функции не являются ни чётными, ни нечётными.

5)Периодичность функции.

Функция называется периодической, если существует такое число Р, что для всех значений аргумента из области определения

у(х + Р) = у(х).

 

 

Линейная функция, её свойства и график.

Линейной функцией называется функция вида y = kx + b, заданная на множестве всех действительных чисел.

k – угловой коэффициент (действительное число)

b – свободный член (действительное число)

x – независимая переменная.

· В частном случае, если k = 0, получим постоянную функцию y = b, график которой есть прямая, параллельная оси Ox, проходящая через точку с координатами (0; b).

· Если b = 0, то получим функцию y = kx, которая является прямой пропорциональностью.

 

o Геометрический смысл коэффициента b – длина отрезка, который отсекает прямая по оси Oy, считая от начала координат.

o Геометрический смысл коэффициента k – угол наклона прямой к положительному направлению оси Ox, считается против часовой стрелки.

 

Свойства линейной функции:

1) Область определения линейной функции есть вся вещественная ось;

2) Если k ≠ 0, то область значений линейной функции есть вся вещественная ось.

Если k = 0, то область значений линейной функции состоит из числа b;

3) Четность и нечетность линейной функции зависят от значений коэффициентов k и b.

a) b ≠ 0, k = 0, следовательно, y = b – четная;

b) b = 0, k ≠ 0, следовательно y = kx – нечетная;

c) b ≠ 0, k ≠ 0, следовательно y = kx + b – функция общего вида;

d) b = 0, k = 0, следовательно y = 0 – как четная, так и нечетная функция.

4) Свойством периодичности линейная функция не обладает;

5) Точки пересечения с осями координат:

Ox: y = kx + b = 0, x = -b/k, следовательно (-b/k; 0) – точка пересечения с осью абсцисс.

Oy: y = 0k + b = b, следовательно (0; b) – точка пересечения с осью ординат.

Замечание. Если b = 0 и k = 0, то функция y = 0 обращается в ноль при любом значении переменной х. Если b ≠ 0 и k = 0, то функция y = b не обращается в ноль ни при каких значениях переменной х.

6) Промежутки знакопостоянства зависят от коэффициента k.

a) k > 0; kx + b > 0, kx > -b, x > -b/k.

y = kx + b – положительна при x из (-b/k; +∞),

y = kx + b – отрицательна при x из (-∞; -b/k).

b) k < 0; kx + b < 0, kx < -b, x < -b/k.

y = kx + b – положительна при x из (-∞; -b/k),

y = kx + b – отрицательна при x из (-b/k; +∞).

c) k = 0, b > 0; y = kx + b положительна на всей области определения,

k = 0, b < 0; y = kx + b отрицательна на всей области определения.

7) Промежутки монотонности линейной функции зависят от коэффициента k.

k > 0, следовательно y = kx + b возрастает на всей области определения,

k < 0, следовательно y = kx + b убывает на всей области определения.

8) Графиком линейной функции является прямая. Для построения прямой достаточно знать две точки. Положение прямой на координатной плоскости зависит от значений коэффициентов k и b.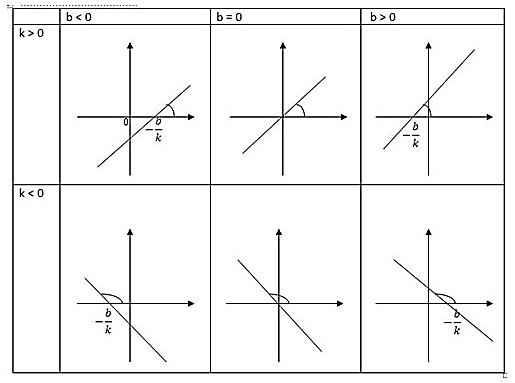

11. Функция у = ах² + bх + с, её свойства и график.

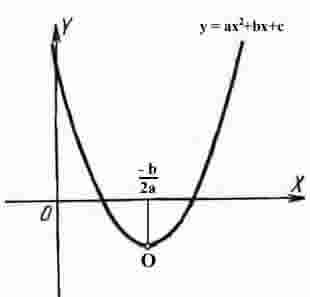
Функция у = ах2 + bх + с (а, b, с - постоянные величины, а ≠ 0) называется квадратичной. В простейшем случае у = ах2 (b = с = 0) график есть кривая линия, проходящая через начало координат. Кривая, служащая графиком функции у = ах2, есть парабола. Каждая парабола имеет ось симметрии, называемую осью параболы. Точка О пересечения параболы с ее осью называется вершиной параболы.

График можно строить по следующей схеме: 1) Находим координаты вершины параболы х0 = -b/2a; у0 = у(х0). 2) Строим еще несколько точек, которые принадлежат параболе, при построении можно использовать симметрии параболы относительно прямой х = -b/2a. 3) Соединяем обозначены точки плавной линией. Пример. Построить график функции в = х2 + 2х - 3. Решения. Графиком функции является парабола, ветви которой направлены вверх. Абсцисса вершины параболы х0 = 2/(2 ∙1) = -1, ее ординаты y(-1) = (1)2 + 2(-1) - 3 = -4. Итак, вершина параболы - точка (-1; -4). Составим таблицу значений для нескольких точек, которые размещены справа от оси симметрии параболы - прямой х = -1.   x       y -3     Обозначим точки, координаты которых записанные в таблице, и точки, симметричные им относительно прямой х = -1. Соединяем точки плавной линией и получим график функции у = х2 + 2х - 3 (рис. 73). .

 

Свойства функции.

Поделиться:

Воспользуйтесь поиском по сайту: