 |
Оценивание погрешностей прямых однократных измерений.
|
|
|
|
Классификация измерений.
1. По характеристике точности измерения делятся на равноточные и неравноточные.
Равноточными измерениями физической величины называется ряд измерений некоторой величины, сделанных при помощи средств измерений (СИ), обладающих одинаковой точностью, в идентичных исходных условиях.
Неравноточными измерениями физической величины называется ряд измерений некоторой величины, сделанных при помощи средств измерения, обладающих разной точностью, и (или) в различных исходных условиях.
2. По количеству измерений измерения делятся на однократные и многократные.
Однократное измерение - это измерение одной величины, сделанное один раз. Однократные измерения на практике имеют большую погрешность, в связи с этим рекомендуется для уменьшения погрешности выполнять минимум три раза измерения такого типа, а в качестве результата брать их среднее арифметическое.
Многократные измерения - это измерение одной или нескольких величин, выполненное четыре и более раз. Многократное измерение представляет собой ряд однократных измерений. Минимальное число измерений, при котором измерение может считаться многократным, - четыре. Результатом многократного измерения является среднее арифметическое результатов всех проведенных измерений. При многократных измерениях снижается погрешность.
3. По типу изменения величины измерения делятся на статические и динамические.
Статические измерения - это измерения постоянной, неизменной физической величины. Примером такой постоянной во времени физической величины может послужить длина земельного участка.
Динамические измерения - это измерения изменяющейся, непостоянной физической величины.
|
|
|
4. По предназначению измерения делятся на технические и метрологические.
Технические измерения - это измерения, выполняемые техническими средствами измерений.
Метрологические измерения - это измерения, выполняемые с использованием эталонов.
5. По способу представления результата измерения делятся на абсолютные и относительные.
Абсолютные измерения - это измерения, которые выполняются посредством прямого, непосредственного измерения основной величины и (или) применения физической константы.
Относительные измерения - это измерения, при которых вычисляется отношение однородных величин, причем числитель является сравниваемой величиной, а знаменатель - базой сравнения (единицей). Результат измерения будет зависеть от того, какая величина принимается за базу сравнения.
6. По методам получения результатов измерения делятся на прямые, косвенные, совокупные и совместные.
Прямые измерения - это измерения, выполняемые при помощи мер, т. е. измеряемая величина сопоставляется непосредственно с ее мерой. Примером прямых измерений является измерение величины угла (мера - транспортир).
Косвенные измерения - это измерения, при которых значение измеряемой величины вычисляется при помощи значений, полученных посредством прямых измерений, и некоторой известной зависимости между данными значениями и измеряемой величиной.
Совокупные измерения - это измерения, результатом которых является решение некоторой системы уравнений, которая составлена из уравнений, полученных вследствие измерения возможных сочетаний измеряемых величин.
Совместные измерения - это измерения, в ходе которых измеряется минимум две неоднородные физические величины с целью установления существующей между ними зависимости.
Методы измерений.
Совокупность приемов использования принципов и средств измерений составляет метод измерения. Различные методы измерений отличаются прежде всего организацией сравнения измеряемой величины с единицей измерения. С этой точки зрения все методы измерений подразделяются на две группы: методы непосредственной оценки и методы сравнения. Методы сравнения в свою очередь включают в себя метод противопоставления, дифференциальный метод, нулевой метод, метод замещения и метод совпадений.
|
|
|
При методе непосредственной оценки значение измеряемой величины определяют непосредственно по отсчетному устройству измерительного прибора прямого действия (измерительный прибор, в котором предусмотрено одно или несколько преобразований сигнала измерительной информации в одном направлении, т. е. без обратной связи). На этом методе основаны все показывающие (стрелочные) приборы (вольтметры, амперметры, ваттметры, счетчики электрической энергии, термометры, тахометры и т. п.). При использовании данного метода измерений мера как вещественное воспроизведение единицы измерения, как правило, непосредственно в процессе измерения не участвует. Сравнение измеряемой величины с единицей измерения осуществляется косвенно путем предварительной градуировки измерительного прибора с помощью образцовых мер или образцовых измерительных приборов.
Точность измерения по методу непосредственной оценки в большинстве случаев невелика и ограничивается точностью применяемых измерительных приборов.
Метод сравнения с мерой - это такой метод измерений, в котором измеряемую величину сравнивают с величиной, воспроизводимой мерой. Примеры этого метода: измерение массы на рычажных весах с уравновешиванием гирь; измерение напряжения постоянного тока на компенсаторе сравнением с ЭДС нормального элемента.
Метод сравнения с мерой, в котором измеряемая величина и величина, воспроизводимая мерой, одновременно воздействуют на прибор сравнения, с помощью которого устанавливается соотношение между этими величинами, называется методом противопоставления. Это, например, измерение массы на рычажных весах с помещением ее и уравновешивающих гирь на две чашки весов при известном соотношении плеч рычага весов. В этом случае при качественном выполнении устройства сравнения (малое трение в опорах, стабильность соотношения плеч рычага и т. п.) может быть достигнута высокая точность измерений (например - аналитические весы).
|
|
|
Дифференциальный метод - это метод сравнения с мерой, в котором на измерительный прибор воздействует разность измеряемой величины и известной величины, воспроизводимой мерой. Этот метод позволяет получать результаты измерений с высокой точностью даже в случае применения относительно неточных измерительных приборов, если с большой точностью воспроизводится известная величина.
Эффект повышения точности результатов измерений, достигаемый при дифференциальном методе, оказывается тем значительнее, чем ближе значение меры к истинному значению измеряемой величины. В том случае, когда результирующий эффект воздействия величин на прибор сравнения доводя до нуля, дифференциальный метод измерений превращается в нулевой. В нулевом методе измерений используемая мера должна быть изменяемой (регулируемой), а прибор сравнения выполняет функции индикатора равенства нулю результирующего воздействия измеряемой величины и меры.
Нулевой метод позволяет получить высокие точности измерений и широко используется, например, при измерениях электрического сопротивления мостом с полным его уравновешиванием или постоянного напряжения компенсатора постоянного тока.
Методом замещения называется метод сравнения с мерой, в котором измеряемую величину замещают известной величиной, воспроизводимой мерой. Это, например, взвешивание с поочередным помещением массы и гирь на одну и ту же чашку весов. Метод замещения можно рассматривать как разновидность дифференциального или нулевого метода, отличающуюся тем, что сравнение измеряемой величины с мерой производится разновременно.
Метод совпадений - это метод сравнения с мерой, в котором разность между измеряемой величиной и величиной, воспроизводимой мерой, измеряют, используя совпадения отметок шкал или периодических сигналов. Примерами этого метода являются измерения длины с помощью штангенциркуля с нониусом, измерение частоты вращения стробоскопом.
|
|
|
Погрешности измерений.
Абсолютная погрешность - это значение, вычисляемое как разность между значением величины, полученным в процессе измерений, и настоящим (действительным) значением данной величины.
Абсолютная погрешность вычисляется по следующей формуле:
ΔQn =Qn ΔQ0,
где AQn - абсолютная погрешность;
Qn - значение некой величины, полученное в процессе измерения;
Q0 - значение той же самой величины, принятое за базу сравнения (настоящее значение).
Абсолютная погрешность меры - это значение, вычисляемое как разность между числом, являющимся номинальным значением меры, и настоящим (действительным) значением воспроизводимой мерой величины.
Относительная погрешность - это число, отражающее степень точности измерения.
Относительная погрешность вычисляется по следующей формуле:
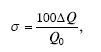
где ΔQ - абсолютная погрешность;
Q0 - настоящее (действительное) значение измеряемой величины.
Относительная погрешность выражается в процентах.
Приведенная погрешность - это значение, вычисляемое как отношение значения абсолютной погрешности к нормирующему значению.
Нормирующее значение определяется следующим образом:
1) для средств измерений, для которых утверждено номинальное значение, это номинальное значение принимается за нормирующее значение;
2) для средств измерений, у которых нулевое значение располагается на краю шкалы измерения или вне шкалы, нормирующее значение принимается равным конечному значению из диапазона измерений. Исключением являются средства измерений с существенно неравномерной шкалой измерения;
3) для средств измерений, у которых нулевая отметка располагается внутри диапазона измерений, нормирующее значение принимается равным сумме конечных численных значений диапазона измерений;
4) для средств измерения (измерительных приборов), у которых шкала неравномерна, нормирующее значение принимается равным целой длине шкалы измерения или длине той ее части, которая соответствует диапазону измерения. Абсолютная погрешность тогда выражается в единицах длины.
Погрешность измерения включает в себя инструментальную погрешность, методическую погрешность и погрешность отсчитывания. Причем погрешность отсчитывания возникает по причине неточности определения долей деления шкалы измерения.
Инструментальная погрешность - это погрешность, возникающая из-за допущенных в процессе изготовления функциональных частей средств измерения ошибок.
Методическая погрешность - это погрешность, возникающая по следующим причинам:
|
|
|
1) неточность построения модели физического процесса, на котором базируется средство измерения;
2) неверное применение средств измерений.
Субъективная погрешность - это погрешность возникающая из-за низкой степени квалификации оператора средства измерений, а также из-за погрешности зрительных органов человека, т. е. причиной возникновения субъективной погрешности является человеческий фактор.
Погрешности по взаимодействию изменений во времени и входной величины делятся на статические и динамические погрешности.
Статическая погрешность - это погрешность, которая возникает в процессе измерения постоянной (не изменяющейся во времени) величины.
Динамическая погрешность - это погрешность, численное значение которой вычисляется как разность между погрешностью, возникающей при измерении непостоянной (переменной во времени) величины, и статической погрешностью (погрешностью значения измеряемой величины в определенный момент времени).
По характеру зависимости погрешности от влияющих величин погрешности делятся на основные и дополнительные.
Основная погрешность - это погрешность, полученная в нормальных условиях эксплуатации средства измерений (при нормальных значениях влияющих величин).
Дополнительная погрешность - это погрешность, которая возникает в условиях несоответствия значений влияющих величин их нормальным значениям, или если влияющая величина переходит границы области нормальных значений.
Нормальные условия - это условия, в которых все значения влияющих величин являются нормальными либо не выходят за границы области нормальных значений.
Рабочие условия - это условия, в которых изменение влияющих величин имеет более широкий диапазон (значения влияющих не выходят за границы рабочей области значений).
Рабочая область значений влияющей величины - это область значений, в которой проводится нормирование значений дополнительной погрешности.
По характеру зависимости погрешности от входной величины погрешности делятся на аддитивные и мультипликативные.
Аддитивная погрешность - это погрешность, возникающая по причине суммирования численных значений и не зависящая от значения измеряемой величины, взятого по модулю (абсолютного).
Мультипликативная погрешность - это погрешность, изменяющаяся вместе с изменением значений величины, подвергающейся измерениям.
Надо заметить, что значение абсолютной аддитивной погрешности не связано со значением измеряемой величины и чувствительностью средства измерений. Абсолютные аддитивные погрешности неизменны на всем диапазоне измерений.
Значение абсолютной аддитивной погрешности определяет минимальное значение величины, которое может быть измерено средством измерений.
Значения мультипликативных погрешностей изменяются пропорционально изменениям значений измеряемой величины. Значения мультипликативных погрешностей также пропорциональны чувствительности средства измерений Мультипликативная погрешность возникает из-за воздействия влияющих величин на параметрические характеристики элементов прибора.
Погрешности, которые могут возникнуть в процессе измерений, классифицируют по характеру появления. Выделяют:
1) систематические погрешности;
2) случайные погрешности.
В процессе измерения могут также появиться грубые погрешности и промахи.
Систематическая погрешность - это составная часть всей погрешности результата измерения, не изменяющаяся или изменяющаяся закономерно при многократных измерениях одной и той же величины. Обычно систематическую погрешность пытаются исключить возможными способами (например, применением методов измерения, снижающих вероятность ее возникновения), если же систематическую погрешность невозможно исключить, то ее просчитывают до начала измерений и в результат измерения вносятся соответствующие поправки. В процессе нормирования систематической погрешности определяются границы ее допустимых значений. Систематическая погрешность определяет правильность измерений средств измерения (метрологическое свойство).
Систематические погрешности в ряде случаев можно определить экспериментальным путем. Результат измерений тогда можно уточнить посредством введения поправки.
Способы исключения систематических погрешностей делятся на четыре вида:
1) ликвидация причин и источников погрешностей до начала проведения измерений;
2) устранение погрешностей в процессе уже начатого измерения способами замещения, компенсации погрешностей по знаку, противопоставлениям, симметричных наблюдений;
3) корректировка результатов измерения посредством внесения поправки (устранение погрешности путем вычислений);
4) определение пределов систематической погрешности в случае, если ее нельзя устранить.
Ликвидация причин и источников погрешностей до начала проведения измерений. Данный способ является самым оптимальным вариантом, так как его использование упрощает дальнейший ход измерений (нет необходимости исключать погрешности в процессе уже начатого измерения или вносить поправки в полученный результат).
Для устранения систематических погрешностей в процессе уже начатого измерения применяются различные способы
Оценивание погрешностей прямых однократных измерений.
Прямые однократные измерения с приближенным оцениванием погрешностей
При приближенной оценке погрешностей, как и при точной, необходимо перед началом измерений провести предварительную оценку составляющих погрешности результата измерения. Эту информацию получают из опыта проведения подобных измерений, нормативнотехнической документации на используемые средства измерений и других источников. Если оценка погрешности превышает допустимую, то следует выбрать более точное средство измерений или изменить методику измерения.
В простейшем случае погрешность равна пределу допускаемой абсолютной основной погрешности средства измерения?си, определяемой по нормативно-технической документации, если измерения проводились в нормальных условиях. При этом результат измерения можно записать в виде хи=  ± Δси, т. е. без указания доверительной вероятности, которая подразумевается как РД = 0,95. Если де измерения проводились в условиях, отличающихся от нормальных, то следует определять и учитывать пределы дополнительных погрешностей, а затем суммировать их с основными.
± Δси, т. е. без указания доверительной вероятности, которая подразумевается как РД = 0,95. Если де измерения проводились в условиях, отличающихся от нормальных, то следует определять и учитывать пределы дополнительных погрешностей, а затем суммировать их с основными.
Пример 4./10. Оценить результат и погрешность однократного измерения напряжения на участке электрической цепи сопротивлением R=4 Ом, выполненного вольтметром класса точности 0,5 % с верхним пределом измерения UB= 1,5 В и внутренним сопротивлением RV = 1000 Ом. Показание вольтметра Ux= 0,90 В. Известно, что дополнительные относительные погрешности показаний вольтметра изза влияния магнитного поля и окружающей температуры не превышают соответственно значений δМ.П. = ± 0,75 % и δТ = ± 0,3 % допускаемой предельной относительной погрешности.
Решение. Инструментальную составляющую погрешности измерения определяют основной и дополнительной погрешностями. При показании вольтметра 0,90 В предел допускаемой относительной погрешности вольтметра на этой отметке в процентах равен:
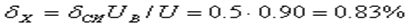
Методическую погрешность определяют соотношением между сопротивлением участка цепи Ru сопротивлением вольтметра RVПри подсоединении вольтметра исходное напряжение Ux изменится из-за наличия сопротивления RV и составит
 (4.49)
(4.49)
Отсюда относительная методическая погрешность:

Эта методическая погрешность является систематической и должна быть исключена из результата измерения путем введения поправки
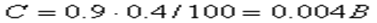
Тогда результат измерения с учетом поправки на систематическую погрешность будет равен
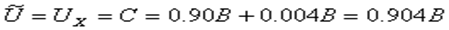
Относительная погрешность результата измерения:
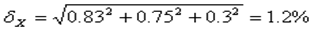
Переходя к абсолютной суммарной погрешности, имеем

Применив статистическое суммирование по (2.42) при РД = 0,95 и коэффициенте К = 1,1, получим значение доверительной границы НСП
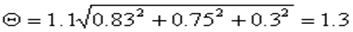
Находим абсолютную погрешность
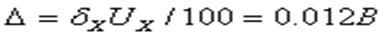
Округляя, окончательный результат измерения представим в виде:


|
|
|


