Алгоритм аппроксимации максимального независимого множества методом исключения подграфов.

 

Авторами данного алгоритма являются Р. Боппана и М. Халлдорсон. Доказательство оценки погрешности можно посмотреть в статье [6].

Введем обозначения: I (G) – максимальное независимое множество, C (G) – максимальная клика.

Под N (v), где v Î G, будем понимать подграф графа G, состоящий из всех вершин и ребер, инцидентных вершине v.

Аналогично, под 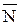(v), где v Î G, будем понимать подграф графа G, состоящий из всех вершин и ребер, не инцидентных вершине v.

Для нахождения максимального независимого множества используется рекурсивный метод, который состоит в следующем: выберем вершину v и занесем её в независимое множество. Построим подграф 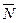(v) (из этого подграфа будут выбираться следующие вершины в независимое множество).

Аналогично сформулируем метод для поиска максимальной клики, с той разницей, что для вершины v ищем подграф N(v), из которого в дальнейшем будут выбираться вершины в максимальную клику.

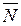Заметим, что при неудачном выборе начальной вершины можно исключить из рассмотрения значительные независимые компоненты (клики). Поэтому предлагается следующая модификация алгоритма. Как и прежде выбираем вершину v, так же находим (v), но на этот раз еще строим граф N (v). Величину независимого множества будем определять, как максимум из величин чисел независимости подграфов N (v) и v È (v). Аналогичный алгоритм работает и для максимальных клик.

Для более точнойаппроксимации независимого множества введем правило выбора вершины v. Вершину будем выбирать с наименьшей степенью, т.к. в этом случае окрестность подобной вершины может содержать более значительное независимое множество. Для максимальной клики вводится аналогичное правило. Здесь в качестве v выбирается вершина с наибольшей степенью.

Фактически алгоритм строит древовидную структуру подзадач, превращая граф в двоичное дерево. Рассмотрим некоторый внутренний узел t этого дерева. Все левые потомки узла t – это вершины, смежные с t, а все правые потомки - несмежные с t вершины. Таким образом, независимое множество вершин, найденное алгоритмом, связано с маршрутом в дереве с самым большим количеством правых потомков. Следовательно, его размер является точным максимальным количеством правых потомков в любом маршруте в дереве, плюс одно. Аналогично, размер найденной клики является максимальным количеством левых потомков в любом маршруте, плюс одно. Введенное правило выбора вершины позволяет удлинить маршрут в дереве с правыми или с левыми потомками в зависимости от того, какую вершину выбираем с минимальной или максимальной степенью вершины для более точной аппроксимации независимого множества или клики.

Например, рассмотрим входной граф G, не содержащий треугольники. Несомненно, алгоритм не может найти клики размера более чем 2, и, следовательно, все маршруты в дереве имеют не более одного левого потомка. Из этого следует также, что самый правый маршрут имеет узлов, либо в дереве менее маршрутов. Но и тогда один из них имеет более чем узлов. В любом случае алгоритм находит независимое множество размера не менее чем .

Выполнение алгоритма, который находит клику размера s и независимое множество размера t, соответствует двоичному дереву, где наибольшее число левых потомков в некотором маршруте – (s – 1) и наибольшее количество правых потомков – (t – 1). Пусть r (s, t) обозначает минимальное целое p такое, что все деревья размера p имеют маршруты с большим количеством либо левых, либо правых потомков. Эта величина больше, чем размер самого большого дерева, в котором нет маршрута с (s – 1) левым потомком или (t – 1) правым. Но эта величина меньше, чем количество листьев в таком дереве. Поскольку каждый лист имеет связанный уникальный маршрут, то в дереве может быть не более чем таких узлов. Следовательно, r(s, t) < .

Пусть R (s,t) (число Рамсея) обозначает минимальное целое n так что все графы размера n или содержат независимое множество размера t или клику размера s. Верхнюю оценку числа Рамсея доказали Эрдеш и Шекереш[7] в 1935:

R(s,t) £ r(s,t) £ .

Отсюда следует, что описанный алгоритм (авторы назвали его Ramsey) находит независимое множество I и клику С такие, что | I | ∙ | C | ≥ (log n)². Реализация алгоритма Ramsey приведена в листинге 12.

 

internal class rebro // класс ребро

{

public int v_na { get; set; }

}

internal class vershina // класс, представляющий вершину в графе

{

public int degree { get; set; } // степень вершины

internal List<rebro> sp_reber; // список инцидентных вершин

public vershina()

{

sp_reber = new List<rebro>();

}

}

public class Graph

{// класс, представляющий граф, заданный списками смежности

internal Dictionary<int, vershina> sp_vershin;

internal int kol_v_n { get; set; }

public Graph()

{

sp_vershin = new Dictionary<int, vershina>();

kol_v_n = 0;

}

// метод возвращающий ключ вершины минимальной степени

public int minDegreeVertex()

{

int nom =-1; // номер вершины минимальной степени

int min; // значение минимальной степени

foreach (KeyValuePair<int, vershina> u in sp_vershin)

{

if(nom == -1)

{

nom = u.Key;

min = u.Value.degree;

}

else if (u.Value.degree < min)

{

nom = u.Key;

min = u.Value.degree;

}

}

return nom;

}

}

internal class resultSet

{ // результирующее множество:

public HashSet<int> clique; // максимальная клика

public HashSet<int> indepSet; // наибольшее незав. мн- во

public resultSet()

{

clique = new HashSet<int>();

indepSet = new HashSet<int>();

}

}

// алгоритм аппроксимации независимого множества вершин class algmApproxIndependentSet // графа

{

resultSet result;

public algmApproxIndependentSet(Graph g)

{

result = Ramsey(g);

Console.WriteLine(" Independence number = "); Console.WriteLine(" {0} ");result.indepSet.Count);

foreach (int v in result.indepSet)

Console.Write("{0} ", v);

}

resultSet Ramsey(Graph g)

{

if (g.kol_v_n == 0)

return new resultSet();

// выберем вершину минимальной степени

int tek_vna = g.minDegreeVertex();

// разделим граф на две части: соседей и не соседей tek_vna

Graph neighbors = buildNeighbGraph(tek_vna, g);

Graph non_neighbors = buildNonNeighbGraph(tek_vna, g);

// вызовем алгоритм Рамсей

resultSet s1 = Ramsey(neighbors);

resultSet s2 = Ramsey(non_neighbors);

// определим наибольшее мн-во

s1.clique.Add(tek_vna);

s2.indepSet.Add(tek_vna);

resultSet rez = new resultSet();

if (s1.clique.Count > s2.clique.Count)

rez.clique = s1.clique;

else rez.clique = s2.clique;

if (s1.indepSet.Count > s2.indepSet.Count)

rez.indepSet = s1.indepSet;

else rez.indepSet = s2.indepSet;

return rez;

}

// метод, который строит граф соседей

Graph buildNeighbGraph(int v_na, Graph g)

{

Graph neighbors = new Graph();

neighbors.kol_v_n = g.sp_vershin[v_na].sp_reber.Count;

// пройдем по списку смежных вершин

// и занесем их в словарь графа соседей

foreach (rebro u in g.sp_vershin[v_na].sp_reber)

{

vershina v = new vershina();

neighbors.sp_vershin.Add(u.v_na, v);

}

// для каждой вершины графа соседей пройдем по списку

// смежных вершин и если смежная вершина принадлежит графу

// соседей, то добавим в граф соседей соответствующее ребро

foreach (KeyValuePair<int, vershina> p in neighbors.sp_vershin)

{

foreach (rebro u in g.sp_vershin[p.Key].sp_reber)

{

if (neighbors.sp_vershin.ContainsKey(u.v_na))

{

rebro r = new rebro { v_na = u.v_na };

p.Value.sp_reber.Add(r);

}

}

p.Value.degree = p.Value.sp_reber.Count;

}

return neighbors;

}

// метод, который строит граф несоседей

Graph buildNonNeighbGraph(int v_na, Graph g)

{

Graph non_neighbors = new Graph();

// пройдем по списку всех вершин графа и, если их нет

// в списке смежных вершин текущей, то занесем их в словарь

// графа несоседей

foreach (KeyValuePair<int, vershina> p in g.sp_vershin)

{

bool flag = true;

foreach(rebro r in g.sp_vershin[v_na].sp_reber)

{

if (r.v_na == p.Key)

flag = false;

}

if (flag && (p.Key!= v_na))

{

vershina u = new vershina();

non_neighbors.sp_vershin.Add(p.Key, u);

}

}

non_neighbors.kol_v_n = non_neighbors.sp_vershin.Count;

// для каждой вершины графа несоседей пройдем по списку

// смежных вершин и если смежная вершина принадлежит графу

// несоседей, то добавим в граф несоседей соответствующее

// ребро

foreach (KeyValuePair<int, vershina> p in non_neighbors.sp_vershin)

{

foreach (rebro u in g.sp_vershin[p.Key].sp_reber)

{

if (non_neighbors.sp_vershin.ContainsKey(u.v_na))

{

rebro r = new rebro { v_na = u.v_na };

p.Value.sp_reber.Add(r);

}

}

p.Value.degree = p.Value.sp_reber.Count;

}

return non_neighbors;

}

}

Листинг 12. Алгоритм апроксимации независимого множества

Вершинное покрытие

 

Введем еще одно понятие, связанное с понятием независимости. Будем говорить, что вершина и ребро графа покрывают друг друга, если они инцидентны. Таким образом, ребро e = { u, v } покрывает вершины u и v, a каждая из этих вершин покрывает ребро e.

Подмножество V ' V (G) называется вершинным покрытием графа G, если каждое ребро из E (G) инцидентно хотя бы одной вершине из V '. Покрытие графа G называется минимальным, если оно не содержит покрытия с меньшим числом вершин, и наименьшим, если число вершин в нем наименьшее среди всех покрытий графа G.

Задача о вершинном покрытии и независимом множестве тесно связаны друг с другом. Множество U вершин графа G является наименьшим (минимальным) покрытием тогда и только тогда, когда U’ = V(G)\ U – наибольшее независимое множество.

Действительно, каждое ребро графа G по определению инцидентно какой-либо вершине в покрытии U. Поэтому невозможно существование ребра, обе вершины которого принадлежали бы множеству V(G)\ U. Таким образом, множество V(G)\ U является независимым. И минимизация множества U равносильна максимизации множества V(G)\ U, то есть эти две задачи эквивалентны. Следовательно, задача поиска минимального вершинного покрытия является NP -полной. Но с помощью очень простого алгоритма можно быстро найти покрытие, которое, самое большее, вдвое больше оптимального.

Выберем в графе произвольное ребро { u, v }, добавим обе вершины u, v к вершинному покрытию, удалим все ребра, имеющие общую вершину с этим ребром, и повторяем этот процесс до тех пор, пока в графе не останется больше ребер.

Очевидно, что данный алгоритм строит вершинное покрытие. Теперь докажем, почему любое другое покрытие имеет не более чем в два раза меньшее количество вершин.

Рассмотрим ребра, выбранные алгоритмом. Ни одна пара этих ребер не может иметь общую вершину. Поэтому любое оптимальное покрытие должно содержать по одной вершине на каждое выбранное ребро, следовательно, оно меньше не более чем в два раза.

Возможно более естественным кажется иной эвристический алгоритм, например, при выборе ребра включать только одну вершину из двух, но на графе К _1,n при неудачном выборе вершины получим покрытие до n -1 вершин, когда наш алгоритм выдаст две вершины. Или если рассмотреть «жадный» алгоритм, и каждый раз включать в вершинное покрытие вершину наибольшей степени, то на графе К _1,n он будет работать идеально, но в случае выбора между одинаковыми или почти одинаковыми вершинами, может значительно отклониться от правильного решения. При этом его трудоемкость хуже, так как необходимо каждый раз упорядочивать вершины по степени.

Дополнительным преимуществом простых эвристических алгоритмов является то, что их часто можно модифицировать для получения лучших практических решений. Например, после окончания работы алгоритма провести операцию по удалению ненужных вершин из покрытия, что позволит получить лучший результат.

 

Паросочетания

 

Не менее важным, чем понятие вершинной независимости, является понятие реберной независимости.

Произвольное подмножество попарно несмежных ребер графа называется паросочетанием (или независимым множеством ребер).

Паросочетание графа G называется максимальным, если оно не содержится в паросочетании с большим числом ребер, и наибольшим, если число ребер в нем наибольшее среди всех паросочетаний графа G.

При изучении паросочетаний основное внимание будет уделяться двудольным графам. Для поиска паросочетаний в произвольном графе используются те же идеи, что и в случае двудольных, только реализация их усложняется.

Задача поиска максимального паросочетания в двудольном графе имеет множество практических приложений. В качестве примера можно рассмотреть паросочетание множества компьютеров K и множества задач T, которые должны выполняться одновременно. Наличие в графе ребра { u, v } означает, что машина u Î K может выполнять задачу v Î T. Максимальное паросочетание обеспечивает максимальную загрузку компьютеров.

Задача построения наибольших паросочетаний в графе изучалась многими исследователями, и для ее решения имеются эффективные алгоритмы, основанные на методе чередующихся цепей Дж. Петерсена.

Пусть M – паросочетание в графе G. Цепь графа G, ребра которой поочередно входят и не входят в M, называется чередующейся относительно M. Цепь длины 1 по определению также чередующаяся. Ребра цепи называются темными или светлыми, если они входят или соответственно не входят в M. Вершины графа G, инцидентные ребрам из M, называются насыщенными, все другие вершины – ненасыщенными. Очевидно, что если в графе G существует чередующаяся относительно паросочетания M цепь, соединяющая две несовпадающие ненасыщенные вершины, то можно построить в G паросочетание с большим числом ребер, чем в M. В самом деле, в такой цепи число темных ребер на единицу меньше числа светлых.

Удалив из M все темные ребра и присоединив все светлые, получим новое паросочетание, в котором число ребер на единицу больше. По этой причине чередующуюся относительно паросочетания M цепь, соединяющую две различные ненасыщенные вершины, будем называть увеличивающейся относительно М цепью в графе G.

Отсутствие увеличивающихся относительно M цепей необходимо, если паросочетание M наибольшее. Поэтому разработка эффективного алгоритма сводится к построению процедуры, которая быстро находит увеличивающую цепь в графе либо выявляет ее отсутствие.

Пусть G = (X, Y, E) – двудольный граф и M – паросочетание в этом графе. Поставим в соответствие графу G и паросочетанию M вспомогательный ориентированный двудольный граф такой что ребра графа G, входящие в паросочетание M, соответствуют в дугам направленнымот Y к X, а все остальные ребра соответствуют дугам направленнымот X к Y.

Обозначим через X_M и Y_M множества ненасыщенных вершин, входящих соответственно в X и Y. Очевидно, что в графе G увеличивающаяся относительно паросочетания M цепь существует тогда и только тогда, когда в графе существует (s, t)- путь, у которого s Î X_M, t Î Y_M.

Пусть – (s, t) путь в графе , s Î X_M, t Î Y_M, P – соответствующая увеличивающаяся цепь в графе G и M ₁ – паросочетание, полученное изменением M вдоль цепи P. Тогда вспомогательный граф ₁ для графа G и паросочетания M ₁ можно получить из графа заменой каждой дуги пути на обратную. Эта операция вместе с поиском пути составляет итерацию приводимого алгоритма.

Предполагается, что граф G задан списками смежности.

Алгоритм построения наибольшего паросочетания в двудольном графе.

1. Построить какое-либо максимальное паросочетание M в графе G.

2. По графу G и паросочетанию M построить граф .

3. Выполнить в графе поиск в ширину из множества X_M вершин, не насыщенных текущим паросочетанием.

4. Если в результате поиска в ширину ни одна из вершин множества Y_M не получила метки, то перейти к п. 5. Иначе перейти к п. 6.

5. Наибольшее паросочетание M ^* равно множеству всех дуг, выходящих из множества Y. Конец.

6. Пусть – (s, t) путь в графе такой, что s Î X_M, t Î Y_M. Изменить граф , заменив в нем каждую дугу (a, b) пути на дугу (b, a). Перейти к п. 2.

Вместе с наибольшим паросочетанием алгоритм фактически находит и наименьшее вершинное покрытие в графе G. В результате последнего выполнения п. 3 алгоритма будет установлено отсутствие пути из X_M в Y_M в графе G. Следовательно, только часть вершин этого графа будет иметь метки после окончания поиска в ширину из X_M. Обозначим через X ' и Y ' соответственно множества непомеченных вершин доли X и помеченных вершин доли Y. Положим Z = X ' È Y '. Множество Z является наименьшим вершинным покрытием графа G.

Трудоемкость алгоритма построения наибольшего паросочетания составляет O (m ∙min{| X |,| Y |}). Действительно, на каждой итерации алгоритма, кроме последней, размер множеств X_M и Y_M уменьшается на единицу. Поэтому общее число итераций не больше min{| X |,| Y |}. Поиск в ширину(п. 3 алгоритма) выполняется за O (m).

Упражения

 

1. Приведите пример графа, на котором алгоритм построения наибольшего независимого множества путем выбора вершин минимальной степени дает не лучший результат.

2. Подмножество V ' вершин графа G называется доминирующим, если каждая вершина из V(G) \ V ' смежна с некоторой вершиной из V '. Докажите, что независимое множество является максимальным (не обязательно наибольшим) тогда и только тогда, когда оно доминирующее.

Приведите пример графа, в котором доминирующее множество не является независимым.

3. Верно ли, что любое паросочетание графа содержится в наибольшем паросочетании?

4. Напишите реализацию алгоритма поиска наибольшего паросочетания в двудольном графе.

Список литературы

1. Кормен Т., Лейзерсон Ч., Ривест Р., Штайн К. Алгоритмы: построение и анализ. 2-е изд. Пер. с англ. – М: Вильямс, 2011. – 1296 с.

2. Кристофидес Н. Теория графов. Алгоритмический подход. – М.: Мир, 1978. – 434 с.

3. Седжвик Р. Фундаментальные алгоритмы на С++. Алгоритмы на графах. Пер. с англ. – СПб: Диасофт, 2002. – 496 с.

4. Скиена С. Алгоритмы. Руководство по разработке. – 2-е изд.: Пер. с англ. – СПб.:БХВ-Петербург, 2011.– 720 с.

5. Троелсен Э. С# и платформа.NET 3.0, специальное издание. –СПб: Питер, 2008. – 1456 с.

6. R. Boppana, M Halldorsson // Approximating maximum independent sets by excluding subgraphs, Bit 32, 2, June 1992

7. P. Erdős, G. Szekerres, // A combinatorial problem in geometry, Compositio Math., 2:463-470,1935.

⇐ Предыдущая1234567

Поделиться:

Воспользуйтесь поиском по сайту: