 |
Найти площадь фигуры, ограниченной линиями
|
|
|
|
Семестр.
1. Основные понятия, связанные с функциями нескольких переменных
2. Частные производные функции 2-х переменных, геометрический смысл
3. Полное приращение и полный дифференциал функции 2-х переменных
4. Градиент, производная по направлению
5. Экстремумы функции 2-х переменных, необходимое и достаточное условия существования
6. Понятие первообразной, свойства, геометрический смысл неопределенного интеграла
7. Методы вычисления неопределенного интеграла
а) интегрирование по частям
б) замена переменной
8. Интегрирование рациональных дробей
9. Интегрирование иррациональностей
10. Интегрирование тригонометрических функций
11. Абстрактное определение определённого интеграла
12. Свойства определённого интеграла
13. Интеграл с переменным верхним пределом, теорема о производной интеграла с переменным верхним пределом.
14. Формула Ньютона –Лейбница
15. Методы вычисления определённого интеграла
16. Несобственные интегралы
17. Приложения определённого интеграла
а) вычисление площадей в декартовых и полярных координатах
б) вычисление длины дуги
в) вычисление объема тела через площадь поперечного сечения и объём тел вращения.
18. Понятие обыкновенных дифференциальных уравнений. ДУ первого порядка. Теорема существования и единственности. Задача Коши (без док-ва).
19. ДУ с разделяющимися переменными.
20. Однородные ДУ первого порядка, нулевая функция однородности.
21. Линейные ДУ. Метод Бернулли.
22. Линейные ДУ. Метод Лагранжа (метод вариации произвольной постоянной).
23. ДУ высших порядков, основные понятия. Теорема существования и единственности. Задача Коши.
24. Линейные однородные ДУ второго порядка.
|
|
|
25. Понятие линейной зависимости и независимости функций. Определитель Вронского.
26. Теорема о структуре общего решения ЛОДУ.
27. ЛОДУ второго порядка с постоянными коэффициентами. Метод характеристического уравнения.
28. Линейные неоднородные дифференциальные уравнения. Теорема о структуре общего решения.
29. ЛНДУ второго порядка. Метод вариации произвольных постоянных.
30. ЛНДУ второго порядка с постоянными коэффициентами и правой частью специального вида.
- Системы дифференциальных уравнений.
- Понятие двойного интеграла (определения, теорема существования без доказательства, свойства).
- Вычисление двойного интеграла.
- Замена переменной в двойном интеграле.
- Приложения двойного интеграла.
Семестр
Дифференциальное исчисление ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
1. Найти область определения функций:

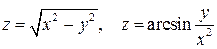
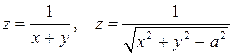



2. Найти частные производные от функций:
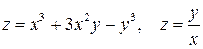


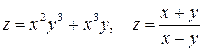



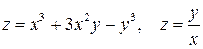
3. Дана функция z=f(x,y), точка М(х,у) и вектор 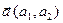 . Найти градиент и производную по направлению вектора
. Найти градиент и производную по направлению вектора  в точке М.
в точке М.
1. z=xy-2x2+4y-5; M(2,3),  (2,-1)
(2,-1)
2 z= 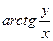 ; M (2, 2),
; M (2, 2),  (-3, 4)
(-3, 4)
3. z=  ; M(-1, 2),
; M(-1, 2),  (-2,1)
(-2,1)
4. z=  ; M(2, 1),
; M(2, 1),  (4,-3)
(4,-3)
5. z=  ; M(4,3),
; M(4,3),  (-2,3)
(-2,3)
Найти наибольшее и наименьшее значение функции в замкнутой области Д.
1. z=x2-2x+y2-2у+2; Д: 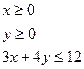
2. z=x3+y3-3ху; Д: 
3. z=x2у(4-x-у); Д: 
4. z=x2+2xу-4х+3у; Д: 
5. z=x3 +y3+3ху; Д: 
5) Дана функция  . Доказать, что
. Доказать, что  .
.
6) Дана функция  . Доказать, что
. Доказать, что  .
.
7) Дана функция  . Доказать, что
. Доказать, что  .
.
8) Дана функция 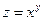 . Доказать, что
. Доказать, что  .
.
9) Найти экстремумы функции 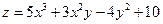 .
.
10) Найти экстремумы функции 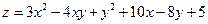 .
.
11) Найти уравнение касательной плоскости и уравнение нормали к поверхности 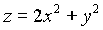 в точке
в точке 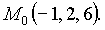 .
.
12) Найти уравнение касательной плоскости и нормали к поверхности 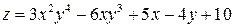 в точке M0(−2;1;20).
в точке M0(−2;1;20).
13) Разложить по формуле Тейлора второго порядка функцию двух переменных  в окрестности точки (-2;1).
в окрестности точки (-2;1).
Неопределенный и определенный интегралы
А. Метод подведения под знак дифференциала
1.  2.
2. 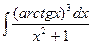 3.
3.  4.
4.  5.
5. 
6.  7.
7.  8.
8.  9.
9. 
10.  11.
11.  12.
12.  13.
13. 
14.  15.
15. 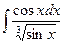 16.
16. 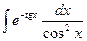 17.
17.  18.
18.  19.
19.  20.
20.  21.
21.  22.
22. 
|
|
|
23. 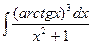 24.
24.  25.
25. 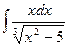 26.
26.  27.
27. 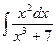
28.  29.
29.  30.
30. 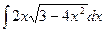 31.
31.  32.
32. 
33.  34.
34. 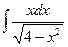 35.
35. 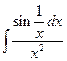 36.
36.  37.
37. 
38.  39.
39. 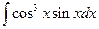 40.
40.  41.
41. 
Б. Метод интегрирования по частям
42.  43.
43. 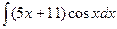 44.
44. 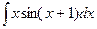 45.
45. 
46.  47.
47.  48.
48.  49.
49. 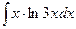 50.
50.  51.
51.  52.
52.  53.
53.  54.
54. 
55.  56.
56. 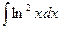 57.
57.  58.
58.  59.
59.  (x+12)cos
(x+12)cos 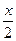 dx 60.
dx 60.  61.
61. 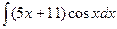 62.
62.  63.
63. 
64. 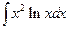 65.
65.  66.
66.  67.
67.  68.
68. 
69. 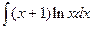 70.
70.  71.
71. 
В. Метод замены переменной
72. 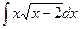 73.
73.  74.
74.  75.
75.  76.
76. 
77.  78.
78. 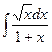 79.
79. 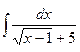 80.
80.  81.
81. 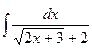
82.  83.
83.  . 84.
. 84.  85.
85.  86.
86. 
87.  88.
88.  89.
89.  90.
90.  91.
91. 
92.  93.
93. 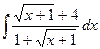 94.
94.  95.
95.  96.
96. 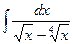
Приложения определенного интеграла
Найти площадь фигуры, ограниченной линиями
1. y=4x2, 9 y=x2, y=2 2. xy=4, y=4x, 4y=x, x>0,y>0
3. 9x=5y2, x=y2-4 4. x=2y-y2, y=lnx, y=2, y=0
5. y=2x, y=2x-x2, x=0, x=2 6. xy=1, y=2x, 2y=x, x>0, y>0
7. y=x2+x-2, x+y=1 8. y=ex, y=lnx, x+y=1, x=3
9. y=cosx, y=-x+3, x=0, y=0 10. 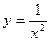 ;
; 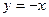 ,x=-2
,x=-2
11. y=ex, y=lnx, x+y=1, x=3 12. y=2x, y=2x-x2, x=0, x=2
13. y=sinx, y=1, x=0 14. y=x2+x-2, x+y=1
15.  , x=8, y=0 15. y=4x2, 9 y=x2, y=2
, x=8, y=0 15. y=4x2, 9 y=x2, y=2
16. Y=x2-1; 2x-y+2=0 17. Y=-x2-2x+3; y=3-4x
18. Y=x2-3x+2; y=x+2 19.Y=5-x2; x-y+3=0
20. Y=x2-6x+5; y=2x-7 21. Y=x2+x-2; x+y=1
22. Y=-x2-6x+5; y=2x-4 23.Y=3x2+1; y=3x+7
24. Y=9-x2; y=x+3 25. Y=x2; y=x+2
26. y = x 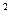 -2x+1, 2x-y-2=0. 27. y = x
-2x+1, 2x-y-2=0. 27. y = x 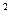 -3x+1, x-y-1=0.
-3x+1, x-y-1=0.
28. y = x 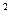 -3x, x-y-3=0. 29. y = x
-3x, x-y-3=0. 29. y = x 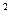 -5x+4, x+y-1=0.
-5x+4, x+y-1=0.
30. y = x 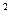 -2x-3, 2x-y-6=0. 31. y = x
-2x-3, 2x-y-6=0. 31. y = x 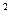 -x-2, 3x-y-5=0.
-x-2, 3x-y-5=0.
32. y = x 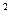 -6x+5, 2x+y-2=0. 33. y = x
-6x+5, 2x+y-2=0. 33. y = x 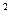 -6x+8, 2x+y-5=0.
-6x+8, 2x+y-5=0.
|
|
|


