 |
Вычисление определителей второго и третьего порядка
|
|
|
|
КУРСОВОЙ ПРОЕКТ
По курсу: Информатика
На тему:
Разработка программы решения системы линейных уравнений
Выполнил: студент
1 курса 3 годичной
заочной формы обучения
(внебюджет)
________ группы
Специальность: ГиМУ
Воищев Алексей Юрьевич
г. Хабаровск 2005
Содержание
Введение
1. Описание математических методов решения систем линейных уравнений
1.1 Метод Гаусса
1.2 Матричный метод
1.3 Вычисление определителей второго и третьего порядка
2. Язык программирования Паскаль
2.1 Структура программы
2.2 Описание переменных
2.3 Основные конструкции языка
2.4 Структуры данных
2.4 Процедуры и функции
3. Описание программы
3.1 Работа программы
3.2 Блок-схема программы
Заключение
Заключение
Список используемых источников и литературы
Приложение
Введение
Последние десятилетия характеризуются бурным развитием вычислительной техники. Расширяются области применения вычислительных машин и совершенствуются методы их использования. Созданы универсальные языки программирования и разработаны мощные операционные системы.
Сейчас невозможно представить себе какую-либо область деятельности, обходящуюся без применения компьютерной техники. Компьютеры используются при проведении различных инженерных расчетов, при решении экономических задач, в процессе управления производством, при получении оценок производственных ситуаций и во многих других случаях.
Системы линейных уравнений появляются почти в каждой области прикладной математики. В некоторых случаях эти системы уравнений непосредственно составляют ту задачу, которую необходимо решать, в других случаях задача сводится к такой системе.
|
|
|
Чтобы быстро справится с решением системы линейных уравнений, можно воспользоваться средствами вычислительной техники - составить программу на языке программирования.
В данной курсовой работе рассматривается возможность решения систем линейных уравнений матричным способом и методом Гаусса с помощью программы, созданной на языке Паскаль.
Описание математических методов решения систем линейных уравнений
Метод Гаусса
Идея метода Гаусса состоит в последовательном исключении неизвестных. Алгоритм решения системы уравнений этим методом проследим на примере.
Пример 1. 
Выбирается ведущее уравнение с коэффициентом при х1, равным 1. В нашем примере ведущим уравнением будет второе. Систему лучше переписать, поставив это уравнение на первое место:
Умножаем первое уравнение на 6 и вычитаем из полученного второе, чтобы исключить из второго неизвестное х1. Первое уравнение записываем, а на место второго - результат вычитания.
Затем первое уравнение умножим на 3 и складываем с третьим уравнением. Тогда получаем систему
Или
первое уравнение переписываем без изменения, а второе умножаем на 7 и вычитаем из него третье уравнение, умноженное на 15, чтобы избавиться от х2 в третьем уравнении. При этом второе записываем без изменения, на месте третьего - результат вычитания. Тогда
Из третьего следует х3 =-3, подставим его во второе, получим х2 = - 2. Далее подставим найденные х2 и х3 в первое уравнение, получим х1 = 1.
Решение системы: х1 = 1, х2 = - 2, х3= - 3.
Примечание: если система уравнений не содержит уравнения с коэффициентом 1 при х1, тогда исключение х1 из второго и третьего достигается умножением сначала первого на коэффициент второго, а второго на коэффициент первого. Затем умножаем первое на коэффициент третьего, а третье на коэффициент первого. Таким образом при вычитании исключаем х1.
|
|
|
Матричный метод
Запишем систему линейных 3 уравнений с 3 неизвестными
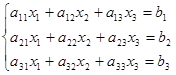
Составим матрицу из коэффициентов при неизвестных
А =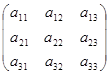 
Введем в рассмотрение матрицы - столбцы для неизвестных и свободных членов:
Х = 
; В =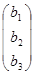 
.
Тогда систему (2) можно переписать в матричной форме
АХ = В
Умножив это уравнение на 
слева, получим 
, откуда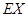 
= 
или 
Следовательно, матрица - решение Х находится как произведение 
на В.
Пример 2. Решить систему уравнений матричным методом
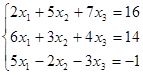
Решение: определитель матрицы
А= 
∆=-1, значит, существует обратная матрица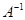 
.
Матрица - столбец при неизвестных:
Х =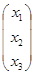 
Матрица - столбец из свободных членов:
В = 
Тогда решение запишется в виде
= = 
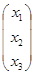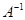
Откуда следует, х1 = 1; х2 = 0; х3 = 2.
Вычисление определителей второго и третьего порядка
Число (а 11 а 22 - а 12 а 21) называется определителем второго порядка и обозначается символом
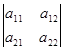
Определитель второго порядка содержит две строки и два столбца. Числа а 11, а 12, а 21, а 22 называются элементами определителя. Диагональ определителя, на которой расположены числа а 11, а 22 - главная, а элементы а 12, а 21 составляют побочную диагональ.
Определитель 3-го порядка содержит три строки и три столбца:
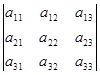
Для вычисления определителя третьего порядка существует несколько способов.
Рассмотрим метод вычисления определителя разложением по элементам первой строки.
Введем понятие минора и алгебраического дополнения.
Минором некоторого элемента определителя называется определитель, полученный из данного вычеркиванием той строки и того столбца в которых этот элемент расположен. Обозначается Мij (i - номер строки, j - номер столбца).
Например, минором элемента а12 является определитель
Алгебраическим дополнением данного элемента определителя называется его минор, умноженный на (-1) i+j. Алгебраические дополнения обозначаются буквами Аij, и тогда Аy= (-1) i+j My.
Определитель вычисляется так:
= 
.
Так же можно разложить определитель по любой строке или столбцу.
Изложенный метод применим к вычислению определителей 4-го и т.д. порядков.
|
|
|
Пример3. Вычислить определитель разложением по элементам первой строки
Решение: Элементы первой строки
а 11 = 1, а 12 = 2, а 13 = - 2.
А11 = (-1) 1+1. М11= 
=4+1=5.
М11 получили, вычеркнув первую строку и первый столбец.
А12 = (-1) 1+2. М12= -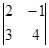 
= - (8+3) = - 11.
М12 получили, вычеркнув первую строку и второй столбец.
А13 = (-1) 1+3. М13 =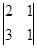 
= 2-3 = - 1.
М13 получили, вычеркнув первую строку и третий столбец.
Окончательно
= 1.5+2. (-11) - 2. (-1) = - 15
|
|
|
