 |
Определение основных характеристик фильтра.
|
|
|
|
Пояснительная записка
К курсовой работе
По электронике
на тему:
«Фильтры верхних частот»
Выполнил:
Студент группы А-144
Безродный С.В.
Проверил:
Христич В.В.
Таганрог 2006
Содержание
1.Техническое задание
2.Получение матрицы
3.Структурная схема
4. Принципиальная схема
5.Расчёт элементов
Расчет звена №1
Расчет звена №2
Расчет звена №3
Расчет звена №4
Расчет звена №5
6.Анализ схемы
7.Определение основных характеристик фильтра
8. Метод Монте Карло
9. Выбор типов элементов.
10.Вывод по проделанной работе
11.Список используемой литературы.
1. Техническое задание
По заданной таблице, в которой приведены значения элементов матриц симметричных фильтров синтезировать принципиальную схему фильтра верхних частот 5-го порядка, провести анализ полученной схемы, по результатам которого определить параметры фильтра.
Вариант С0515а-22.
Таблица 1.

| 0,8669600 | 
| -0,8694698 |
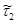
| 1,3527675 | 
| 0,7559777 |

| 1,1890630 | 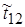
| 0,8618522 |

| 0,7973618 | 
| -0,0106126 |
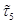
| 0,2867016 | 
| -0,7787701 |
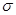 , дБ , дБ
| 0,0988 | 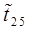
| 0,0079491 |
 , кГц , кГц
| 2,2 | 
| 0,5978956 |
 , дБ , дБ
| 75,59 | 
| -0,3805086 |

| 3,25776 | 
| 0,25 |

| 0,09746 | 
| 1,227…1,191 |

| 0,00049 |
2. Получение матрицы 
Значения элементов  , расположенных ниже главной диагонали, равны по модулю значениям элементов
, расположенных ниже главной диагонали, равны по модулю значениям элементов  , т.е.
, т.е. 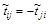 :
:

Для приведения значений элементов к нормированному виду необходимо все элементы каждой i -й строки разделить на  :
:  :
:
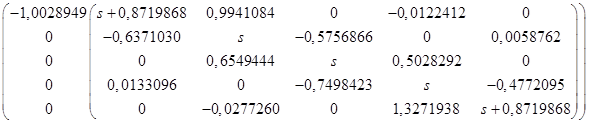
У фильтров наблюдаются динамические перегрузки, когда максимальное напряжение во внутренних узлах схемы превышает максимальное выходное напряжение, что характеризует коэффициент динамической перегрузки. (коэффициент динамической перегрузки на выходе ОУ1  может превышать единицу). Чтобы обеспечить
может превышать единицу). Чтобы обеспечить  , необходимо разделить полученные ранее значения
, необходимо разделить полученные ранее значения  и
и  на
на  :
:
|
|
|

Структурная схема
На основе полученной матрицы строим структурную схему:

Расчёт элементов.
Принципиальную схему ФВЧ синтезируют на основе звеньев:
1) Многовходовое инвертирующее звено ФВЧ:

Рис. 1.
Функция передачи имеет вид: 
Это звено может использоваться только в качестве 1-го или n -го звена при условии, что все матричные элементы соответственно 1-й или n -й строки положительны.
2) Многовходовое универсальное звено ФВЧ:

Рис. 2.
Функция передачи имеет вид:  ;
;  .
.
Зададим значение емкости  всех звеньев одинаковым и равным
всех звеньев одинаковым и равным 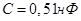 .
.
 .
.
Из выражения постоянной времени 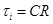 , где
, где  .
.
Так как 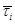 для всех звеньев одинаково и
для всех звеньев одинаково и  , то
, то  .
.
Сопротивление 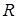 для всех звеньев одинаково.
для всех звеньев одинаково.
Положив  , определим сопротивления резисторов входного сумматора из соотношений:
, определим сопротивления резисторов входного сумматора из соотношений:
 ,
,
где  (
( или
или  ) — коэффициент, который задается равным единице при не слишком малом значении
) — коэффициент, который задается равным единице при не слишком малом значении  (
( или
или  ) и гораздо меньше единицы в противном случае.
) и гораздо меньше единицы в противном случае.
Если сопротивление резистора  или
или  получается слишклм большим, то он заменяется резистивным делителем, состоящим из трех резисторов (см. рис.3.). Чтобы определить сопротивления делителя, необходимо задаться значениями
получается слишклм большим, то он заменяется резистивным делителем, состоящим из трех резисторов (см. рис.3.). Чтобы определить сопротивления делителя, необходимо задаться значениями  и
и  , а эквивалентное сопротивление
, а эквивалентное сопротивление  и сопротивление резистора
и сопротивление резистора  рассчитать из соотношений:
рассчитать из соотношений:
 ;
;  ,
,
где  - это модуль
- это модуль  или
или  . Эквивалентная проводимость
. Эквивалентная проводимость  используется в формулах для
используется в формулах для  и
и  при расчете сопротивления
при расчете сопротивления 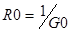 .
.

Рис.3. Резистивный делитель.
Расчет звена №1

 :
:


 :
:


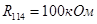 ,
, 

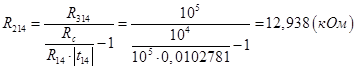

 .
.
Расчет звена №2

 :
:
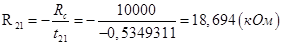 ,
,
 ;
;
 :
:
 ;
;
 ,
,  ,
,
 ,
,
 ,
,
 ,
,
 .
.
Расчет звена №3

 :
:



 .
.
Расчет звена №4

 :
:

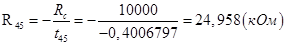
 :
:

 ,
, 


|
|
|

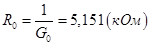 .
.
Расчет звена №5
 :
:
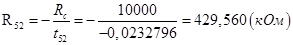 ;
;
 :
:
 ;
;
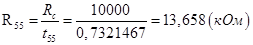 ;
;
 ,
, 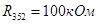 ;
;
 ;
;
 ;
;
 ;
;
 .
.
Так как полученная проводимость  , то резистор
, то резистор  переключаем с инвертирующего на неинвертирующий вход ОУ2.
переключаем с инвертирующего на неинвертирующий вход ОУ2.
Анализ схемы
Используя пакет прикладных программ MicroCap-8, проанализируем данную схему.

Рис. 4. Амплитудно-частотная характеристика с входа на выход.

Рис. 5. АЧХ фильтра в полосе пропускания.
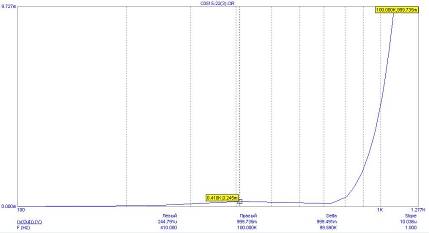
Рис. 6. АЧХ фильтра в полосе режекции.

Рис. 7. АЧХ фильтра в дБ.

Рис. 8. АЧХ с выходов 1,2,3,4 звеньев соответственно.
Как видно из рисунков, динамических перегрузок в фильтре не возникает.
Определение основных характеристик фильтра.
Нижняя граничная частота полосы пропускания:

Нижняя граничная частота полосы режекции:

Максимальный коэффициент передачи:
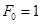
Коэффициент передачи полосы пропускания:

Коэффициент передачи полосы режекции:

Неравномерность АЧХ в полосе пропускания:

Затухание в полосе режекции:

Коэффициент прямоугольности:

Сравним полученные характеристики с табличными:
Таблица 2.
| Параметры | 
| 
| 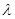
| 
|
| Теоретические | 2,200 | 0,0988 | 75,59 | 3,25776 |
| Фактические | 2,217 | 0,0973 | 72,24 | 3,13254 |
| Погрешность, % | 0,77 | 1,52 | 4,43 | 4,91 |
Метод Монте-Карло
Графики АЧХ, полученные в процессе 200 испытаний методом Монте-Карло в диапазоне частот 0,1…100 кГц при равновероятностном отклонении параметров схемных элементов на 2%.

Рис. 9. АЧХ фильтра при испытании методом Монте-Карло.

Рис. 10. АЧХ фильтра при испытании методом Монте-Карло в полосе пропускания.
Из рисунка 7 видно, что: 
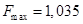 .
.
Гистограмма распределения.

MC-8 GUAP Edition
Monte Carlo AC анализ of C0515-22
200 Runs
Summary
Низкий=0.972
Средний=1.001
Высокий=1.035
Стандартное отклонение=0.013
Статистика индивидуального выполнения.
Таблица 3.
| 1 | 1.013 | 101 | 0.988 |
| 2 | 1.008 | 102 | 1.006 |
| 3 | 1.007 | 103 | 0.979 |
| 4 | 1.005 | 104 | 0.985 |
| 5 | 1.017 | 105 | 1.022 |
| 6 | 1.026 | 106 | 1.000 |
| 7 | 0.994 | 107 | 0.999 |
| 8 | 1.002 | 108 | 1.026 |
| 9 | 0.991 | 109 | 1.007 |
| 10 | 1.006 | 110 | 1.008 |
| 11 | 1.005 | 111 | 1.012 |
| 12 | 0.987 | 112 | 0.996 |
| 13 | 1.008 | 113 | 1.005 |
| 14 | 1.018 | 114 | 1.015 |
| 15 | 0.998 | 115 | 0.985 |
| 16 | 1.020 | 116 | 1.035 |
| 17 | 1.004 | 117 | 0.995 |
| 18 | 0.997 | 118 | 1.013 |
| 19 | 0.993 | 119 | 1.000 |
| 20 | 1.016 | 120 | 1.009 |
| 21 | 1.020 | 121 | 1.006 |
| 22 | 0.997 | 122 | 0.999 |
| 23 | 0.996 | 123 | 1.024 |
| 24 | 0.991 | 124 | 0.990 |
| 25 | 1.000 | 125 | 1.015 |
| 26 | 1.006 | 126 | 1.021 |
| 27 | 1.002 | 127 | 1.021 |
| 28 | 1.000 | 128 | 1.000 |
| 29 | 1.033 | 129 | 0.995 |
| 30 | 0.974 | 130 | 1.018 |
| 31 | 1.013 | 131 | 1.000 |
| 32 | 1.004 | 132 | 0.996 |
| 33 | 1.000 | 133 | 1.005 |
| 34 | 1.006 | 134 | 0.983 |
| 35 | 0.995 | 135 | 1.007 |
| 36 | 0.991 | 136 | 1.004 |
| 37 | 1.006 | 137 | 0.999 |
| 38 | 1.032 | 138 | 1.011 |
| 39 | 1.007 | 139 | 1.015 |
| 40 | 0.982 | 140 | 1.017 |
| 41 | 0.984 | 141 | 1.001 |
| 42 | 0.980 | 142 | 0.988 |
| 43 | 1.010 | 143 | 0.988 |
| 44 | 0.998 | 144 | 0.993 |
| 45 | 1.015 | 145 | 1.015 |
| 46 | 0.990 | 146 | 0.997 |
| 47 | 0.999 | 147 | 1.001 |
| 48 | 1.007 | 148 | 1.018 |
| 49 | 1.021 | 149 | 0.996 |
| 50 | 1.003 | 150 | 0.996 |
| 51 | 1.000 | 151 | 0.981 |
| 52 | 0.997 | 152 | 1.010 |
| 53 | 0.985 | 153 | 1.022 |
| 54 | 0.992 | 154 | 0.983 |
| 55 | 0.998 | 155 | 1.007 |
| 56 | 0.987 | 156 | 0.995 |
| 57 | 1.010 | 157 | 0.985 |
| 58 | 0.972 | 158 | 1.001 |
| 59 | 1.000 | 159 | 0.993 |
| 60 | 0.997 | 160 | 1.000 |
| 61 | 0.998 | 161 | 1.006 |
| 62 | 1.008 | 162 | 1.006 |
| 63 | 1.003 | 163 | 0.981 |
| 64 | 0.993 | 164 | 1.004 |
| 65 | 1.002 | 165 | 1.013 |
| 66 | 1.028 | 166 | 0.997 |
| 67 | 1.012 | 167 | 1.010 |
| 68 | 1.009 | 168 | 1.010 |
| 69 | 0.997 | 169 | 0.996 |
| 70 | 0.988 | 170 | 0.986 |
| 71 | 0.993 | 171 | 0.995 |
| 72 | 1.029 | 172 | 1.001 |
| 73 | 1.002 | 173 | 1.010 |
| 74 | 1.026 | 174 | 0.991 |
| 75 | 1.018 | 175 | 0.981 |
| 76 | 1.002 | 176 | 0.990 |
| 77 | 0.981 | 177 | 1.008 |
| 78 | 0.980 | 178 | 1.001 |
| 79 | 1.012 | 179 | 0.975 |
| 80 | 1.026 | 180 | 0.989 |
| 81 | 1.003 | 181 | 0.999 |
| 82 | 0.984 | 182 | 1.005 |
| 83 | 1.010 | 183 | 0.974 |
| 84 | 0.989 | 184 | 1.005 |
| 85 | 0.994 | 185 | 0.993 |
| 86 | 0.998 | 186 | 0.991 |
| 87 | 0.976 | 187 | 1.012 |
| 88 | 1.032 | 188 | 0.975 |
| 89 | 0.997 | 189 | 1.000 |
| 90 | 1.006 | 190 | 0.988 |
| 91 | 0.983 | 191 | 1.006 |
| 92 | 1.020 | 192 | 1.016 |
| 93 | 1.001 | 193 | 0.986 |
| 94 | 1.006 | 194 | 0.984 |
| 95 | 0.990 | 195 | 1.001 |
| 96 | 1.010 | 196 | 1.010 |
| 97 | 1.011 | 197 | 0.998 |
| 98 | 1.003 | 198 | 1.003 |
| 99 | 1.008 | 199 | 1.004 |
| 100 | 1.006 | 200 | 0.993 |
Выбор типов элементов.
|
|
|
Номиналы резисторов используемых в электрической схеме корректирующего устройства приведены в таблице 4.
В этой таблице приведены следующие параметры:
Расчёт – значения, полученные в результате расчёта;
ГОСТ – значения, резисторов выбранных в соответствии с рядом Е192;
Погрешность – погрешность отклонения от ряда;
ТКС(ТКЕ) – погрешность по температурной нестабильности сопротивления (ёмкости) в интервале от –60 0С до +25 0С;
Допуск – технологическая погрешность элементов;
Суммарная погрешность – общая погрешность элементов.
Таблица 4.
| Наименование (Резистор) | Расчёт, кОм | ГОСТ, кОм | Погрешность, % | ТКС, % | Допуск, % | Суммарная погрешность, % |
| R | 168,943 | 169 | 0,03374 | 0,075 | 0,5 | 0,63599 |
| R 10 | 11,876 | 11,8 | 0,63995 | 0,045 | 0,5 | 1,24130 |
| R 11 | 13,658 | 13,7 | 0,30751 | 0,045 | 0,5 | 0,90886 |
| R 12 | 11,981 | 12 | 0,15858 | 0,045 | 0,5 | 0,75993 |
| R 214 | 12,938 | 12,9 | 0,29371 | 0,045 | 0,5 | 0,89506 |
| R 01 | 27,401 | 27,4 | 0,00365 | 0,045 | 0,5 | 0,60500 |
| R 21 | 18,694 | 18,7 | 0,03210 | 0,045 | 0,5 | 0,63345 |
| R 23 | 20,688 | 20,5 | 0,90874 | 0,045 | 0,5 | 1,51009 |
| R 225 | 5,474 | 5,49 | 0,29229 | 0,045 | 0,5 | 0,89364 |
| R 02 | 5,200 | 5,23 | 0,57692 | 0,045 | 0,5 | 1,17827 |
| R 32 | 9,092 | 9,09 | 0,02200 | 0,045 | 0,5 | 0,62335 |
| R 34 | 14,843 | 14,9 | 0,38402 | 0,045 | 0,5 | 0,98537 |
| R 03 | 179,225 | 180 | 0,43242 | 0,075 | 0,5 | 1,03377 |
| R 43 | 15,883 | 15,8 | 0,52257 | 0,045 | 0,5 | 1,12392 |
| R 45 | 24,958 | 24,9 | 0,23239 | 0,045 | 0,5 | 0,83374 |
| R 241 | 36,492 | 36,1 | 1,07421 | 0,045 | 0,5 | 1,67556 |
| R0 4 | 5,151 | 5,17 | 0,36886 | 0,045 | 0,5 | 0,97021 |
| R 54 | 8,974 | 8,98 | 0,06686 | 0,045 | 0,5 | 0,66821 |
| R 55 | 13,658 | 13,7 | 0,30751 | 0,045 | 0,5 | 0,90886 |
| R 252 | 43,562 | 43,7 | 0,31679 | 0,045 | 0,5 | 0,91814 |
| R 05 | 12,991 | 12,9 | 0,70048 | 0,045 | 0,5 | 1,30183 |
| Rc | 10 | 10 | 0 | 0,045 | 0,5 | 0,60135 |
| R1v, R3v | 100 | 100 | 0 | 0,075 | 0,5 | 0,60225 |
|
|
|

Рис. 11. Резистор типа С2-14.
| Наименование (Конденсатор) | Расчёт, нФ | ГОСТ, нФ | Погрешность, % | ТКЕ, % | Допуск, % | Суммарная погрешность, % |
| С | 0,51 | 0,51 | 0 | 0,15 | 0,5 | 0,50450 |
|
|
|


