Главная | Обратная связь | Поможем написать вашу работу!

Определение оптимальных настроек основного регулятора

Для определения оптимальных настроек основного ПИ-регулятора R(s) основной технологической переменной (выбирается согласно регламента технологического процесса установки в соответствие с вариантом темы курсовой работы) необходимо:

– определить передаточную функцию эквивалентного объекта управления 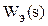, содержащую , , 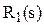по формуле

. (1)

– воспользоваться методом расширенных амплитудофазочастотных характеристик (РАФЧХ).

Переходной процесс в системе не будет содержать составляющих со степенью колебательности выше заданной m, если обеспечивается условие

, (2)

где - РАФЧХ эквивалентного объекта управления;

- РАФЧХ регулятора.

Отсюда

, (3)

где – инверсные РАФЧХ эквивалентного объекта управления.

Таблица 2 – Оптимальные настройки регулятора (инженерная методика)

Регулятор	Настройки	Типовой процесс регулирования
апериодический	с 20 % перерегулированием	с
П	k_Р1
ПИ	k_Р_{1 opt}
Т_И₁ _opt	0,6t₀₁	0,7t₀₁	t₀₁
ПИД	k_Р_{1 opt}
Т _И1_opt	2,4t₀₁	2t₀₁	1,3t₀₁
Т_Д_{1 opt}	0,4t₀₁	0,4t₀₁	0,5t₀₁

Методика расчета РАФЧХ эквивалентного объекта управления W_Э(m, jw) заключается в следующем.

3.2.1 Для расчета РАФЧХ в выражении передаточной функции эквивалентного объекта управления W_Э(s ) s заменяют на (-mw+jw), выделяют действительную и мнимую части.

Для получения РАФЧХ эквивалентного объекта управления можно воспользоваться пакетом прикладной программы MathCAD.

3.2.2 Оптимальные настройки ПИ-регулятора k_Р, определяют из выражений:

; (4)

, (5)

где , - инверсные значения действительной и мнимой части РАФЧХ эквивалентного объекта управления.

3.2.3 Для получения инверсных значений и необходимо воспользоваться соотношениями:

; (6)

. (7)

3.2.4 Задавшись значениями , строят график линии равного значения степени колебательности m k_u(k_Р),при этом

. (8)

Оптимальные настройки выбирают в точке соответствующей максимуму k_u.

Качество переходного процесса каскадной автоматической системы регулирования определяют с помощью прикладных пакетов MATLAB, MathCAD.

Литература [13],[14], [15]

Пример расчета оптимальных настроек каскадной автоматической системы регулирования

Исходные данные

c, k_u = 15, T_u = 4,5 с – время запаздывания, коэффициент усиления и постоянная времени технологического объекта управления с передаточной функцией W_u(s).

с, k₀₁= 3, T₀₁= 2 с – время запаздывания, коэффициент усиления и постоянная времени технологического объекта управления с передаточной функцией W₀₁(s).

– степень колебательности;

, с – оптимальные настройки внутреннего вспомогательного ПИ-регулятора c передаточной функцией R₁(s) получены по таблице 2 для апериодического переходного процесса.

Заданное значение вспомогательной технологической переменной в относительных единицах: yd₁=1, заданное значение основной технологической переменной yd=(1 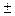0,05).

Порядок расчета

Для определения оптимальных настроек основного ПИ – регулятора с передаточной функцией воспользуемся выражением для передаточной функции эквивалентного объекта управления согласно (1):

Определение оптимальных настроек и проведем по методу РАФЧХ.

РАФЧХ эквивалентного объекта управления W_Э(m, jw) определяем, заменив в передаточной функции W_Э(s) s -mw+jw.

= (9)

где , , , – модуль и аргумент числителя и знаменателя РАФЧХ эквивалентного объекта управления;

, – модуль и аргумент РАФЧХ эквивалентного объекта управления;

, – действительная и мнимая части РАФЧХ эквивалентного объекта управления.

Для определения РАФЧХ эквивалентного объекта управления найдем РАФЧХ W_u(s), W₀₁(s), R₁(s):

= =

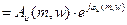; (10)

(11)

(12)

где , – действительная и мнимая части РАФЧХ технологического объекта управления;

, – модуль и аргумент РАФЧХ технологического объекта управления.

Определим РАФЧХ внутреннего вспомогательного регулятора с передаточной функцией R₁(s):

= =

= ; (13)

(14)

(15)

где , – действительная и мнимая части РАФЧХ внутреннего вспомогательного регулятора;

, – модуль и аргумент РАФЧХ внутреннего вспомогательного регулятора.

Определим РАФЧХ технологического объекта управления внутреннего вспомогательного контура регулирования технологической переменной y₁ с передаточной функцией W₀₁(s):

= = ; (16)

(17)

, (18)

где , - действительная и мнимая части РАФЧХ технологического объекта управления W₀₁(s) внутреннего вспомогательного контура регулирования технологической переменной y₁(s);

, - модуль и аргумент РАФЧХ технологического объекта управления W₀₁(s) внутреннего вспомогательного контура регулирования технологической переменной y₁(s).

Определим числитель РАФЧХ эквивалентного объекта управления в показательной форме записи:

(19)

(20)

Определим знаменатель РАФЧХ эквивалентного объекта управления, предварительно рассчитав промежуточные переменные:

(21)

(22)

Тогда действительная и мнимая части знаменателя РАФЧХ эквивалентного объекта управления соответственно равны:

(23)

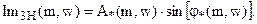(24)

Получим модуль и аргумент знаменателя РАФЧХ эквивалентного объекта управления соответственно:

(25)

(26)

Модуль и аргумент РАФЧХ эквивалентного объекта управления соответственно равны:

(27)

(28)

Действительная и мнимая части РАФЧХ эквивалентного объекта управления соответственно равны:

(29)

(30)

Для получения инверсных значений воспользуемся выражениями (6) и (7):

Настройки основного регулятора можно рассчитать по формулам (4) и (5):

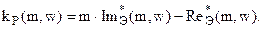
Изменяя значения w согласно (8) при заданном значении m, строим по таблице 3 расчетных значений график равного значения степени колебательности (рисунок 3).

Таблица 3 – Расчетные значения

Рисунок 3 – График равного значения степени колебательности m

Из рисунка 17 видно, что максимум графика равного значения степени колебательности соответствует значениям:

Таким образом, передаточные функции регуляторов выглядят следующим образом:

;

На рисунке 4 представлена математическая модель для исследования динамической характеристики вспомогательной технологической переменной y₁(t) в среде MATLAB, MathCAD.

kp₁ opt

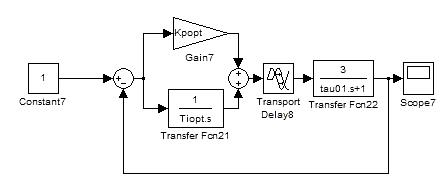
Рисунок 4 – Математическая модель для исследования динамической характеристики y₁(t)

График переходного процесса вспомогательной технологической переменной y₁(t) представлен на рисунке 5.

Рисунок 5 – График переходного процесса технологической переменной y₁(t)

На рисунке 6 представлена математическая модель для исследования динамической характеристики основной технологической переменной y (t) в среде MATLAB, MathCAD.

Рисунок 6 – Математическая модель для исследования динамической характеристики y(t)

График переходного процесса основной технологической переменной y(t)/ представлен на рисунке 7.

Рисунок 7 – График переходного процесса основной технологической переменной y(t)

Показатели качества процесса регулирования основной технологической переменной (перерегулирования, время переходного процесса) можно определить по графику рисунка 7, зная требуемую точность регулирования, руководствуясь исходными данными.

⇐ Предыдущая 12

Воспользуйтесь поиском по сайту: