 |
Сопряжение окружностей (дуг)
|
|
|
|
Внешнее сопряжение дуг окружностей
Внешним сопряжением считается сопряжение, при котором центры сопрягаемых окружностей (дуг) O1 (радиус R1) и O2 (радиус R2) располагаются за сопрягающей дугой радиуса R. На примере рассмотрено внешнее сопряжение дуг (рис.5). Сначала находим центр сопряжения. Центром сопряжения является точка пересечения дуг окружностей с радиусами R+R1 и R+R2, построенных из центров окружностей O1(R1) и O2(R2) соответственно. Затем центры окружностей O1 и O2 соединяем прямыми с центром сопряжения, точкой O, и на пересечении линий с окружностями O1 и O2 получаем точки сопряжения A и B. После этого, из центра сопряжения строим дугу заданного радиуса сопряжения R и соединяем ей точки A и B.

Рисунок 5. Внешнее сопряжение дуг окружностей
Внутреннее сопряжение дуг окружностей
Внутренним сопряжением называется сопряжение, при котором центры сопрягаемых дуг O1, радиуса R1, и O2, радиус R2, располагаются внутри сопрягающей их дуги заданного радиуса R. На рис.6 приведён пример построения внутреннего сопряжения окружностей (дуг). Вначале мы находим центр сопряжения, которым является точка O, точка пересечения дуг окружностей с радиусами R-R1 и R-R2 проведённых из центров окружностей O1 и O2 соответственно. После чего соединяем центры окружностей O1 и O2 прямыми линиями с центром сопряжения и на пересечении линий с окружностями O1 и O2 получаем точки сопряжения A и B. Затем из центра сопряжения строим дугу сопряжения радиуса R и строим сопряжение.
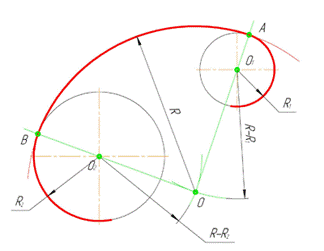 Рисунок 6. Внутреннее сопряжение дуг окружностей
Рисунок 6. Внутреннее сопряжение дуг окружностей
|  Рисунок 7.Смешанное сопряжение дуг окружностей
Рисунок 7.Смешанное сопряжение дуг окружностей
|
Смешанное сопряжение дуг окружностей
Смешанным сопряжением дуг является сопряжение, при котором центр одной из сопрягаемых дуг (O1) лежит за пределами сопрягающей их дуги радиуса R, а центр другой окружности(O2) – внутри её. На рис.7 приведён пример смешанного сопряжения окружностей. Сначала находим центр сопряжения, точку O. Для нахождения центра сопряжения строим дуги окружностей с радиусами R+ R1, из центра окружности радиуса R1 точки O1, и R-R2, из центра окружности радиуса R2 точки O2. После чего соединяем центр сопряжения точку O с центрами окружностей O1 и O2 прямыми и на пересечении с линиями соответствующих окружностей получаем точки сопряжения A и B. Затем строим сопряжение.
|
|
|
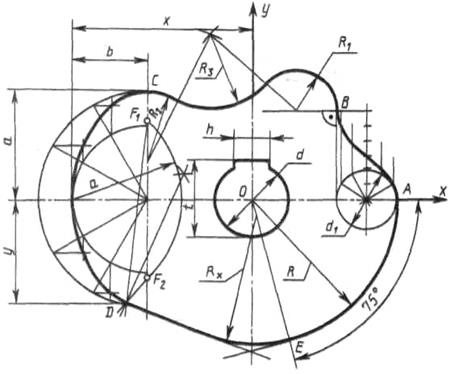
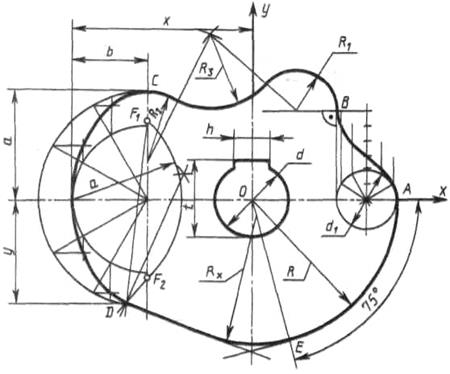
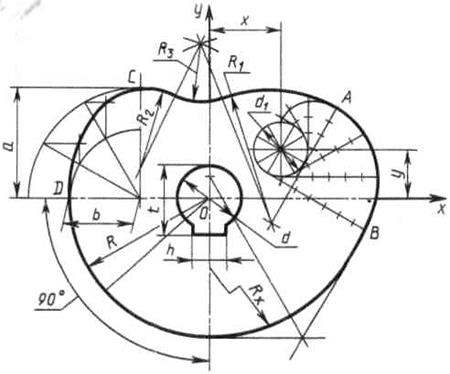
Построение кулачка
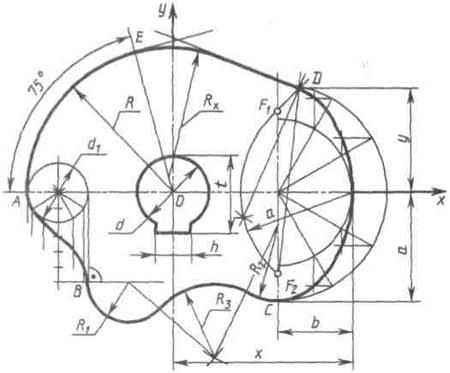
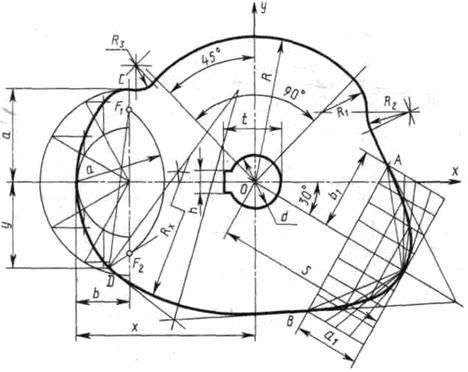
Построение очертания кулачка в каждом варианте следует начинать с нанесения осей координат Ох и Оу. Затем строят лекальные кривые по их заданным параметрам и выделяют участки, входящие в очертание кулачка. После этого можно вычертить плавные переходы между лекальными кривыми. При этом следует учесть, что во всех вариантах через точку D проходит касательная к эллипсу.
Обозначение Rx показывает, что величина радиуса определяется построением. На чертеже вместо Rx надо проставить соответствующее число со знаком «*».
Лекальной называют кривую, которую нельзя построить с помощью циркуля. Ее строят по точкам с помощью специального инструмента, называемого лекалом. К лекальным кривым относятся эллипс, парабола, гипербола, спираль Архимеда и др.
Среди закономерных кривых наибольший интерес для инженерной графики представляют кривые второго порядка: эллипс, парабола и гипербола, с помощью которых образуются поверхности, ограничивающие технические детали.
Эллипс - кривая второго порядка. Одним из способов построения эллипса является способ построения эллипса по двум осям рис.8. При построении проводим окружности радиусами r и R из одного центра О и произвольную секущую ОА. Из точек пересечения 1 и 2 проводим прямые, параллельные осям эллипса. На их пересечении отмечаем точку М эллипса. Остальные точки строим аналогично.
|
|
|
 Рисунок 8. Способ построения эллипса по двум осям
Рисунок 8. Способ построения эллипса по двум осям
|
 Рисунок 9. Построение параболы
Рисунок 9. Построение параболы
|
Параболой называется плоская кривая, каждая точка которой расположена на одинаковом расстоянии от заданной прямой, носящей название директрисы, и точки называемой фокусом параболы, расположенных в той же плоскости.
На рисунке 9 приведен один из способов построения параболы. Даны вершина параболы О, одна из точек параболы А и направление оси – ОС. На отрезке ОС и СА строят прямоугольник, стороны этого прямоугольника в задании – А1 и В1, делят на произвольное одинаковое число равных частей и нумеруют точки деления 1, 2, 3, 4… 10. Вершину О соединяют с точками деления на А1, а из точек деления отрезка В1 проводят прямые параллельные оси ОС. Пересечение прямых, проходящих через точки с одинаковыми номерами, определяют ряд точек параболы.
Синусоидой называют плоскую кривую, изображающую изменение синуса в зависимости от изменения его угла. Для построения синусоиды (рис. 10) нужно разделить окружность на равные части и на такое же количество равных частей разделить отрезок прямой АВ = 2лR. Из одноименных точек деления провести взаимно перпендикулярные линии, в пересечении которых получают точки, принадлежащие синусоиде.
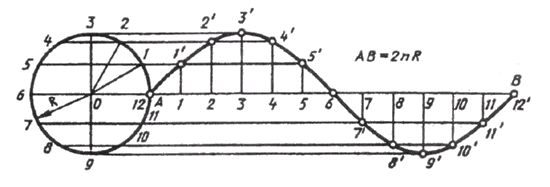
Рисунок 10. Построение синусоиды
Эвольвентой называют плоскую кривую, являющуюся траекторией любой точки прямой линии, перекатываемой по окружности без скольжения. Построение эвольвенты выполняют в следующем порядке (рис.11): окружность делят на равные части; проводят касательные к окружности, направленные в одну сторону и проходящие через каждую точку деления; на касательной, проведенной через последнюю точку деления окружности, откладывают отрезок, равный длине окружности 2 л R, который делят на столько же равных частей. На первой касательной откладывают одно деление 2 л R/n, на второй – два и т.д.
 Рисунок 11. Построение эвольвенты
Рисунок 11. Построение эвольвенты
|
 Рисунок 12. Спираль Архимеда
Рисунок 12. Спираль Архимеда
|
Спираль Архимеда – плоская кривая, которую описывает точка, движущаяся равномерно-поступательно от центра О по равномерно вращающемуся радиусу (рис.12).
|
|
|
Для построения спирали Архимеда задается шаг спирали – а, и центр О. Из центра О описывают окружность радиусом Р = а (0-8). Делят окружность на несколько равных частей, например, на восемь (точки 1, 2, …, 8). На столько же частей делят отрезок О8. Из центра О радиусами О1, О2, и т.д. проводят дуги окружностей, точки пересечения которых с соответствующими радиусами-векторами принадлежат спирали (I, II, …,YIII)
Таблица 2
 Кулачок Кулачок
| ||||||||||||||||||||||||||
 Кулачок Кулачок
|
 Кулачок
Кулачок
| ||||||||||||||||||||||||||||
 Кулачок
Кулачок
|
 Кулачок
Кулачок
| ||||||||||||||||||||||||||||||
 Кулачок
Кулачок
|
 Кулачок
Кулачок
| ||||||||||||||||||||||||||||||
 Кулачок
Кулачок
|
 Кулачок
Кулачок
| ||||||||||||||||||||||||||
 Кулачок
Кулачок
|
 Кулачок
Кулачок
| ||||||||||||||||||||||||||
 Кулачок Кулачок
|
 Кулачок
Кулачок
| ||||||||||||||||||||||||||||
 Кулачок
Кулачок
|
|
|
|
 Кулачок
Кулачок
| ||||||||||||||||||||||||||||||
 Кулачок
Кулачок
|
 Кулачок
Кулачок
| ||||||||||||||||||||||||||||||
 Кулачок
Кулачок
|
|
|
|


