 |
Многогранники. Как построить точку, линию на поверхности многогранника?
|
|
|
|
Виды проецирования
1. Центральное проецирование – проецирующие лучи выходят из одной точки (центра). Размеры предмета на плоскости проекций искажаются.
2. Параллельное проецирование – проецирующие лечи параллельны и составляют с плоскостью угол 90% (прямоугольное проецирование) и угол отличный от 90 % (косоугольное проецирование).
Инвариантные свойства параллельного проецирования
- Проекция точки есть точка;
- Проекция прямой есть прямая;
- Если точка К принадлежит прямой а, то и проекция этой точки
принадлежит проекции прямой;
- Если точка К делит отрезок АD в отношении m: n то и проекция
этой точки делит в таком же отношении проекцию этого отрезка;
- Проекция точки пересечения прямых есть точка пересечения проек
ций этих прямых;
- Проекции параллельных прямых параллельны;
-Плоский многоугольник в общем случае проецируется в многоугольник с тем же числом вершин;
- Прямая, параллельная направлению проецирования, проецируется в точку;
- Проекция плоской фигуры, параллельной плоскости проекций, конгруэнтна этой фигуре.
Следствия этого инвариантного свойства следующие:
1. Проекция отрезка прямой, параллельной плоскости проекций, конгруэнтна и параллельна самому отрезку.
2. Проекция угла, стороны которого параллельны плоскости проекций, конгруэнтна этому углу.
Какими координатами определяется горизонтальная, фронтальная, профильная проекции точки?
Горизонтальная проекция a1 определяется координатами х и у, фронтальная проекция a2 — координатами х и z, профильная проекция a3 — координатами у и z.
Какая прямая называется прямой общего, частного положения.
- Если отрезок [AB], определяющий прямую l занимает произвольное положение по отношению к плоскостям проекций (угла наклона прямой l к плоскостям проекций отличаются от 0° и 90°), то такая прямая называется прямой общего положения.
|
|
|
- Прямые частного положения - это прямые, параллельные одной или двум плоскостям проекций.
В первом случае прямые называются прямыми уровня.
Во втором случае - проецирующими прямыми, т.к. перпендикулярны какой-нибудь плоскости проекций.
Как определить по комплексному чертежу взаимное положение двух прямых?
- Параллельные прямые. Проекции двух параллельных прямых параллельны между собой.
Для профильных прямых для определения параллельности прямых, необходимо, чтобы все три проекции прямых были параллельны, т.к. две проекции профильной прямой не определяют параллельность.
- Пересекающиеся прямые. Если прямые линии пересекаются, то п. одноименные проекции пересекаются между собой в точке, которая является проекцией точкой пересечения этих прямых.
Необходимым и достаточным условием является лишь то, чтобы точки пересечения одноименных проекций находились на одном перпендикуляре к соответствующей оси проекций.
- Скрещивающиеся прямые. Скрещивающиеся прямые линии не пересекаются и не параллельны между собой. Хотя одноименные проекции и пересекаются между собой, но точки их пересечения не могут быть соединены линией связи, т.е. эти прямые не пересекаются между собой Точки пересечения одноименных проекции скрещивающихся прямых представляют собой проекции двух точек, из которых одна принадлежит первой, а другая - второй из этих скрещивающихся прямых.
5. Какая плоскость называется плоскостью общего, частного положения? Приведите примеры.
- Плоскость частного положения - плоскость проходящая через проецирующие прямые, т.е. перпендикулярная к одной или одновременно к двум основным плоскостям проекций. Если плоскость перпендикулярна только к одной плоскости проекций, то она называется проецирующей плоскостью;
|
|
|
- Плоскость общего положения - плоскость не перпендикулярная ни к одной из плоскостей проекций. Рассмотрим пример комплексного чертежа плоскости общего положения, заданной тремя точками, не лежащими на одной прямой: А, В, С, т. е. треугольник АВС. Спроецируем точки А, В, С на все три плоскости проекций, и получим ортогональные проекции плоскости, заданной треугольником АВС. Каждая проекция плоскости АВС, есть треугольник.
Как могут быть расположены в пространстве друг относительно друга точка, прямая и плоскость?
-Точка принадлежит отрезку, если ее проекции располагаются на одноименных проекциях этой же прямой.
-Отрезок прямой относительно плоскостей проекций может быть:
-отрезком общего положения (углы наклона отрезка к плоскостям проекций произвольные);
-отрезком уровня (параллельным какой-либо плоскости проекций);
-проецирующим отрезком (перпендикулярным какой-либо плоскости проекций).
-Отрезок может быть задан как в системе p1p 2, так и в p1p2p3.
-По двум заданным проекциям всегда можно построить третью.
-Отрезок в пространстве характеризуется длиной и углом наклона к плоскостям проекций.
-Для отрезков уровня и проецирующих эти величины определяются на самом комплексном чертеже, так как одна из проекций отрезка частного положения есть его натуральная величина.
-Для нахождения натуральной величины отрезка общего положения и углов его наклона к плоскостям проекций применяется метод прямоугольного треугольника.
Как определить по комплексному чертежу, принадлежит ли точка прямой, плоскости?
-Прямая может принадлежать и не принадлежать плоскости. Она принадлежит плоскости, если хотя бы две точки ее лежат на плоскости.
-Если прямая не принадлежит плоскости, она может быть параллельной ей или пересекать ее.
-Прямая параллельна плоскости, если она параллельна другой прямой, лежащей в этой плоскости.
-Прямая может пересекать плоскость под различными углами и, в частности, быть перпендикулярной ей.
-Точка по отношению к плоскости может быть расположена следующим образом: принадлежать или не принадлежать ей. Точка принадлежит плоскости, если она расположена на прямой, расположенной в этой плоскости.
|
|
|
Многогранники. Как построить точку, линию на поверхности многогранника?
-При работе с комплексным чертежом многогранника приходится строить на его поверхности линии, а так как линия есть совокупность точек, то необходимо уметь строить точки на поверхности.
-Любую точку на гранной поверхности можно построить с помощью образующей, проходящей через эту точку.
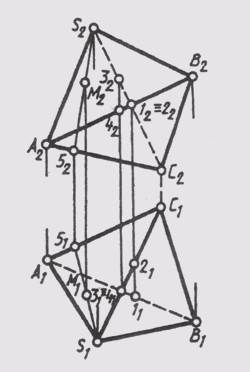На рис. в грани ACS построена точка М с помощью образующей S-5.
|
|
|
