Как построить точку пересечения прямой и плоскости?

Нахождение точки пересечения прямой и плоскости является одной из основных задач начертательной геометрии. Эта задача, как вспомогательная, входит в решение более сложных задач на пересечение поверхностей плоскостью, на построение линии пересечения двух поверхностей и т.п.

В зависимости от положения прямой и плоскости относительно плоскостей проекций можно выделить три задачи на построение точки встречи прямой и плоскости:

- пересечение проецирующей плоскости с прямой общего положения;
- пересечение плоскости общего положения с проецирующей прямой;
- пересечение плоскости общего положений с прямой общего положения.

7.2.1.Построение точки встречи прямой общего положения с проецирующей плоскостью

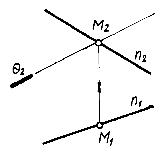Рис. 7.4.

В качестве примера построим точку встречи фронтально проецирующей плоскости Q с прямой общего положения n (рис.7.4). Пусть n Ç Q = = М. М₂ - фронтальная проекция искомой точки М должна лежать на фронтальной проекции П₂ прямой n, как точка, принадлежащая прямой n. В то же время фронтальная проекция М₂ точки М должна лежать на следе Q₂ плоскости Q, так как искомая точка принадлежит и плоскости Q. Следовательно, искомая фронтальная проекция М₂ точки М может лежать только на пересечении n₂ иQ₂. Имея фронтальную проекцию М₂ точки М, при помощи линии связи легко найти ее горизонтальную проекцию.

7.2.2.Построение точки встечи плоскости общего положения с проецирующей прямой

Рис. 7.5.

На рис.7.5 показано построение точки встречи горизонтально проецирующей прямой n с плоскостью общего положения Q (a Ç b). Горизонтальные проекции всех точек, принадлежащих данной прямой, в том числе и горизонтальная проекция М₁ искомой точки М, будут совпадать с n₁ - горизонтальной проекцией прямой n. Следовательно, задача сводится к нахождению недостающей фронтальной проекции М₁ точки М, лежащей в плоскости Q. Через М₁ проведем прямую 1₁2₁. По линиям связи найдем фронтальные проекции 1₂, 2₂ точек 1и 2, через которые проведем фронтальную проекцию прямой 12. На пересечении 1₂2₂ с n₂ и будет находиться фронтальная проекция М₂ точки М.

7.2.3.Построение точки встречи прямой общего положения с плоскостью общего положения

Пусть дана некоторая плоскость Q и прямая n (рис.7.6). Требуется построить точку М пересечения данных прямой и плоскости.

Решение этой задачи состоит из трех простейших последовательных операций:

1) через прямую проводят вспомогательную плоскость F;
2) находят линию пересечения 1 данной Q и вспомогательной F плоскостей;
3) отмечают искомую точку М как точку пересечения прямой 1 с данной прямой n.

Пример построения точки встречи прямой общего положения с плоскостью общего положения на комплексном чертеже приведен на рис. 7.7. Заключаем прямую n в горизонтально проецирующую плоскость F (F ₁ º n₁). Находим линию пересечения плоскостей F и Q (F Ç Q = 12). Горизонтальная проекция этой прямой совпадает с горизонтальной проекцией прямой n. Фронтальную проекцию прямой 12 проводим через 1₂ и 2₂, которые находим с помощью линий связи по принадлежности плоскости Q. Отмечаем точку пересечения фронтальных проекций 1₂2₂ и n₂ прямых 12 и n (F (1₂2₂ Ç n₂ = M₂). M₂ является фронтальной проекцией точки встречи прямой n с плоскостью Q. Горизонтальную проекцию строим по линиям связи по принадлежности точки M прямой n.

Видимость прямой n определяем с помощью конкурирующих точек. Конкурирующими называют точки, проекции которых совпадают. Для определения видимости на П₁ в качестве конкурирующих возьмем точки 1 и 3, одна из которых принадлежит прямой ВС, вторая - n. Найдем фронтальные проекции этих точек. Так как точка 1 раположена выше точки 3, то на П₁ мы видим плоскость, а прямую n не видим. В точке пересечения видимость меняется на обратную. Видимость на П₂ находим с помощью конкурирующих точек 4 и 5 аналогично.