 |
Проецирование отрезка прямой линии
|
|
|
|
ВОПРОС 10













ВОПРОС 11
Проецирование отрезка прямой линии
Проецирование отрезка прямой на горизонтальную, фронтальную и профильную плоскости проекции заключается в построении соответствующих проекций двух точек, принадлежащих данной прямой, и проведении прямой линии через одноименные проекции этих точек.
Если какая – либо точка принадлежит прямой, то ее проекция принадлежит проекции прямой.
Относительно плоскостей проекций прямая может занимать различные положения:
не параллельное ни одной из плоскостей проекций;
параллельное одной из плоскостей проекций;
параллельное двум плоскостям проекций, т. е. перпендикулярное третьей.
Прямая, не параллельная ни одной из плоскостей проекций, называется прямой общего положения. Ни одна из проекций прямой общего положения не параллельна оси проекции и не перпендикулярна к ней. При этом каждая из проекций меньше самого отрезка. Натуральную величину отрезка прямой общего положения и углов наклона его к плоскостям проекций можно определить методом прямоугольного треугольника. Прямая, параллельная одной из плоскостей проекций или двум плоскостям проекций, называется прямой частного положения.
Известны следующие прямые частного положения:
горизонтальная прямая – параллельна горизонтальной плоскости; фронтальная проекция отрезка параллельна оси проекций и горизонтальная проекция этого отрезка равна самому отрезку;
фронтальная прямая – параллельна фронтальной плоскости; горизонтальная проекция отрезка параллельна оси проекции и фронтальная проекция этого отрезка равна самому отрезку;
|
|
|
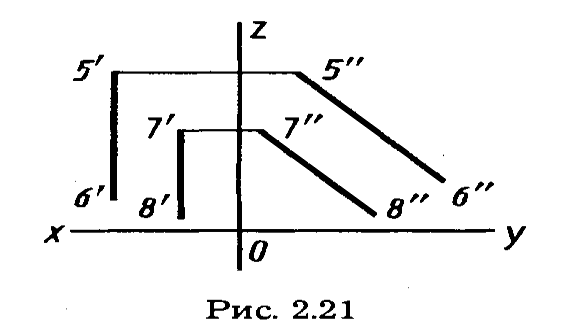
профильная прямая – параллельна профильной плоскости; профильная проекция отрезка равна самому отрезку;
горизонтально-проецирующая прямая –параллельна к фронтальной и профильной плоскостям проекций, т. е. перпендикулярна к горизонтальной плоскости проекций;
фронтально-проецирующая прямая –параллельна к горизонтальной и профильной плоскостям проекций, т. е. перпендикулярна к фронтальной плоскости проекций;
профильно проецирующая прямая –параллельна к горизонтальной и фронтальной плоскостям проекций, т. е. перпендикулярна к профильной плоскости проекций.
Прямая общего положения, пересекает все три плоскости проекций. Точки пересечения прямой с горизонтальной, фронтальной и профильной плоскостями называют соответственно горизонтальным фронтальным и профильным следом прямой.
Положение горизонтального и фронтального следов прямой определяет, в каких четвертях пространства находится тот или иной участок прямой.
Прямая частного положения не пересекает все три плоскости и не имеет следа на той плоскости, которой она параллельна.В частности горизонтальная прямая не имеет горизонтального следа, фронтальная прямая не имеет фронтального следа, горизонтально-проецирующая прямая не имеет фронтального и профильного следов и т. д.
По взаимному положению прямых в пространстве они называются следующим образом:
пересекающиеся прямые;
параллельные прямые;
скрещивающиеся прямые.
Если прямые пересекаются, то их одноименные проекции пересекаются между собой, а проекции точек пересечения лежат на одной линии связи.Скрещивающиеся прямые не пересекаются и не параллельны между собой в пространстве. Точки пересечения одноименных проекций скрещивающихся прямых не лежат на одной линии связи.
На скрещивающихся прямых можно выделить конкурирующие точки, т. е. такие, проекции которых на одной из плоскостей совпадают.
|
|
|
Анализ положения конкурирующих точек позволяет определить, какая из изображенных на чертеже прямых ближе другой к наблюдателю.
Проекция круга
Проекции круга могут быть изображены:

а) окружностью (диаметр которой равен диаметру круга) в том случае, когда плоскость круга параллельна плоскости проекций (фиг246,а);
б) отрезком (размер которого равен диаметру круга) в том случае, когда плоскость круга перпендикулярна плоскости проекций (фиг246,б);
в) эллипсом (бодьшая ось которого равна диаметру круга, а длина малой оси зависит от угла наклона: чем больше угол, тем меньше длина) в том случае, когда плоскость круга находится под некоторым углом к плоскости проекций (фиг246,б).
На (фиг.247) даны примеры проекций круга, выявленных окружностью и отрезком.
1. Круг расположен во фронтальной плоскости (фиг.247,а); его фронтальная проекция - круг, изображенный окружностью; горизонтальная - отрезок, равный диаметру.
2. Круг расположен в горизонтальной плоскости проекций (фиг.247,б); его горизонтальная проекция - круг, изображенный окружностью; фронтальная - отрезок, равный диаметру.
Разберем случай, когда проекция круга выявляется эллипсом.
3. Круг расположен во фронтально - проектирующей плоскости δ, точка О явится его центром; требуется спроектировать круг на плоскости П1 и П2 (фиг.247,в).
По свойству проектирующих плоскостей фронтальная проекция круга - прямая, сливающаяся с проекцией δ2, равная диаметру; горизонтальная проекция - эллипс, так как плоскость δ расположена наклонно к плоскости П1.
Задача сводится к построению на плоскости П1 проекции двух диаметров круга, расположенных параллельно плоскостям П1 и П2 (т.е осей эллипса). Диаметр АВ круга, расположенный параллельно плоскости П2, проектируется на нее отрезком А2В2, равным натуральной величине диаметра круга; на плоскость П1 диаметр круга проектируется отрезком A1B1, величина которого определяется построением и явится малой осью эллипса. Диаметр CD круга, расположенный параллельно плоскости П1 проектируется на нее отрезком C1D1 равным натуральной величине диаметра круга, и явится большой осью эллипса; на плоскость П2 диаметр круга проектируется точкой, сливающейся с проекцией δ2. Имея две оси эллипса, можно построить эллипс, воспользовавшись правилом построения эллипса по двум данным его осям.
|
|
|

Но представляется возможным найти горизонтальные проекции еще нескольких точек, обеспечивающие проведение эллипса.
Для этого проведем вспомогательную окружность радиусом (A2B2)÷2, затем разделим фронтальную проекцию А2В2 на четыре равные части (можно на 6, 8 и т.д.) и через точку О2 проведем перпендикулярно А2B2 диаметр D, а через точки Р2 и Р'2 - хорды k, ему параллельные (фиг.247,г).
На вертикальных линиях связи, проведенных через точки Р1 и Р на плоскости П1 откладываем хорды k, получим дополнительные горизонтальные проекции точек: Е1Е11F2F12 окружности круга. Все точки последовательно соединим плавной кривой. Это будет горизонтальная проекция круга - эллипс.
Все задачи на нахождение положения геометрических элементов в пространстве, не связанные с измерением и метрическими свойствами фигур, например точка на прямой, пересекающиеся прямые, точка и прямая в плоскости и др., называются позиционными задачами.
Проектирование по заранее установленным размерам, например изображение точки по данным: высоте, глубине и широте или изображение плоской фигуры по заданным координатам ее вершин, называется метрической задачей.
3.Проекция винтовой линии





4. Проекция сферы является кругом.
5. Отрезок, разделенный на n равных частей изображается отрезком, разделимым на n равных частей.
6. Проекция параллельных прямых



ВОПРОС 6


|
|
|


