Алгоритм обратного распространения

Самый известный вариант алгоритма обучения нейронной сети - так называемый алгоритм обратного распространения (back propagation). Существуют современные алгоритмы второго порядка, такие как метод сопряженных градиентов и метод Левенберга-Маркара, которые на многих задачах работают существенно быстрее (иногда на порядок). Алгоритм обратного распространения наиболее прост для понимания, а в некоторых случаях он имеет определенные преимущества. Сейчас мы опишем его, а более продвинутые алгоритмы рассмотрим позже. Разработаны также эвристические модификации этого алгоритма, хорошо работающие для определенных классов задач, - быстрое распространение (Fahlman, 1988) и Дельта-дельта с чертой (Jacobs, 1988).

В алгоритме обратного распространения вычисляется вектор градиента поверхности ошибок. Этот вектор указывает направление кратчайшего спуска по поверхности из данной точки, поэтому если мы "немного" продвинемся по нему, ошибка уменьшится. Последовательность таких шагов (замедляющаяся по мере приближения к дну) в конце концов приведет к минимуму того или иного типа. Определенную трудность здесь представляет вопрос о том, какую нужно брать длину шагов.

При большой длине шага сходимость будет более быстрой, но имеется опасность перепрыгнуть через решение или (если поверхность ошибок имеет особо вычурную форму) уйти в неправильном направлении. Классическим примером такого явления при обучении нейронной сети является ситуация, когда алгоритм очень медленно продвигается по узкому оврагу с крутыми склонами, прыгая с одной его стороны на другую. Напротив, при маленьком шаге, вероятно, будет схвачено верное направление, однако при этом потребуется очень много итераций. На практике величина шага берется пропорциональной крутизне склона (так что алгоритм замедляет ход вблизи минимума) с некоторой константой, которая называется скоростью обучения. Правильный выбор скорости обучения зависит от конкретной задачи и обычно осуществляется опытным путем; эта константа может также зависеть от времени, уменьшаясь по мере продвижения алгоритма.

Обычно этот алгоритм видоизменяется таким образом, чтобы включать слагаемое импульса (или инерции). Этот член способствует продвижению в фиксированном направлении, поэтому если было сделано несколько шагов в одном и том же направлении, то алгоритм "увеличивает скорость", что (иногда) позволяет избежать локального минимума, а также быстрее проходить плоские участки.

Таким образом, алгоритм действует итеративно, и его шаги принято называть эпохами. На каждой эпохе на вход сети поочередно подаются все обучающие наблюдения, выходные значения сети сравниваются с целевыми значениями и вычисляется ошибка. Значение ошибки, а также градиента поверхности ошибок используется для корректировки весов, после чего все действия повторяются. Начальная конфигурация сети выбирается случайным образом, и процесс обучения прекращается либо когда пройдено определенное количество эпох, либо когда ошибка достигнет некоторого определенного уровня малости, либо когда ошибка перестанет уменьшаться (пользователь может сам выбрать нужное условие остановки).

Переобучение и обобщение

Одна из наиболее серьезных трудностей изложенного подхода заключается в том, что таким образом мы минимизируем не ту ошибку, которую на самом деле нужно минимизировать, - ошибку, которую можно ожидать от сети, когда ей будут подаваться совершенно новые наблюдения. Иначе говоря, мы хотели бы, чтобы нейронная сеть обладала способностью обобщать результат на новые наблюдения. В действительности сеть обучается минимизировать ошибку на обучающем множестве, и в отсутствие идеального и бесконечно большого обучающего множества это совсем не то же самое, что минимизировать "настоящую" ошибку на поверхности ошибок в заранее неизвестной модели явления (Bishop, 1995).

Сильнее всего это различие проявляется в проблеме переобучения, или слишком близкой подгонки. Это явление проще будет продемонстрировать не для нейронной сети, а на примере аппроксимации посредством полиномов, - при этом суть явления абсолютно та же.

Полином (или многочлен) - это выражение, содержащее только константы и целые степени независимой переменной. Вот примеры:

y=2x+3

y=3x2+4x+1

Графики полиномов могут иметь различную форму, причем чем выше степень многочлена (и, тем самым, чем больше членов в него входит), тем более сложной может быть эта форма. Если у нас есть некоторые данные, мы можем поставить цель подогнать к ним полиномиальную кривую (модель) и получить таким образом объяснение для имеющейся зависимости. Наши данные могут быть зашумлены, поэтому нельзя считать, что самая лучшая модель задается кривой, которая в точности проходит через все имеющиеся точки. Полином низкого порядка может быть недостаточно гибким средством для аппроксимации данных, в то время как полином высокого порядка может оказаться чересчур гибким, и будет точно следовать данным, принимая при этом замысловатую форму, не имеющую никакого отношения к форме настоящей зависимости (см. рис.).

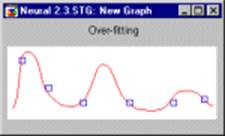
Рис 6 – График полинома

Нейронная сеть сталкивается с точно такой же трудностью. Сети с большим числом весов моделируют более сложные функции и, следовательно, склонны к переобучению. Сеть же с небольшим числом весов может оказаться недостаточно гибкой, чтобы смоделировать имеющуюся зависимость. Например, сеть без промежуточных слоев на самом деле моделирует обычную линейную функцию.

Как же выбрать "правильную" степень сложности для сети? Почти всегда более сложная сеть дает меньшую ошибку, но это может свидетельствовать не о хорошем качестве модели, а о переобучении.

Ответ состоит в том, чтобы использовать механизм контрольной кросс-проверки. Мы резервируем часть обучающих наблюдений и не используем их в обучении по алгоритму обратного распространения. Вместо этого, по мере работы алгоритма, они используются для независимого контроля результата. В самом начале работы ошибка сети на обучающем и контрольном множестве будет одинаковой (если они существенно отличаются, то, вероятно, разбиение всех наблюдений на два множества было неоднородно). По мере того, как сеть обучается, ошибка обучения, естественно, убывает, и, пока обучение уменьшает действительную функцию ошибок, ошибка на контрольном множестве также будет убывать. Если же контрольная ошибка перестала убывать или даже стала расти, это указывает на то, что сеть начала слишком близко аппроксимировать данные и обучение следует остановить. Это явление чересчур точной аппроксимации в процессе обучения и называется переобучением. Если такое случилось, то обычно советуют уменьшить число скрытых элементов и/или слоев, ибо сеть является слишком мощной для данной задачи. Если же сеть, наоборот, была взята недостаточно богатой для того, чтобы моделировать имеющуюся зависимость, то переобучения, скорее всего, не произойдет, и обе ошибки - обучения и проверки - не достигнут достаточного уровня малости.

Описанные проблемы с локальными минимумами и выбором размера сети приводят к тому, что при практической работе с нейронными сетями, как правило, приходится экспериментировать с большим числом различных сетей, порой обучая каждую из них по нескольку раз (чтобы не быть введенным в заблуждение локальными минимумами) и сравнивая полученные результаты. Главным показателем качества результата является здесь контрольная ошибка. При этом, в соответствии с общенаучным принципом, согласно которому при прочих равных следует предпочесть более простую модель, из двух сетей с приблизительно равными ошибками контроля имеет смысл выбрать ту, которая меньше.

Необходимость многократных экспериментов ведет к тому, что контрольное множество начинает играть ключевую роль в выборе модели, то есть становится частью процесса обучения. Тем самым ослабляется его роль как независимого критерия качества модели - при большом числе экспериментов есть риск выбрать "удачную" сеть, дающую хороший результат на контрольном множестве. Для того, чтобы придать окончательной модели должную надежность, часто (по крайней мере, когда объем обучающих данных это позволяет) поступают так: резервируют еще одно - тестовое множество наблюдений. Итоговая модель тестируется на данных из этого множества, чтобы убедиться, что результаты, достигнутые на обучающем и контрольном множествах реальны, а не являются артефактами процесса обучения. Разумеется, для того чтобы хорошо играть свою роль, тестовое множество должно быть использовано только один раз: если его использовать повторно для корректировки процесса обучения, то оно фактически превратится в контрольное множество.