Критические условия хранения различных видов растительного сырья

 

№ п/п	Наиме­нование продук­та
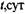
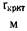
	Травя­ная мука	121-1015		1,75	357,73	-	329,45	-	318,53	-
	Шрот подсол­нечный	3,79- 106	43,2	2,27	267,61	2,4	225,92	2,2	211,84	2,2	0,39
	Жмых подсол­нечный	1,51 106	42,0	1,2	274,44		229,48	3,6	214,50	3,5	0,5
	Шрот соевый	4,36- 109	47,3	1,85	292,61		247,03	9,2	231,64	9,1	0,8
	Мука пшенич­ная	1,94- 1010	81,2	3,02	348,88	-	310,45	-	296,42	1387, 6	8,4
	Отруби пшенич­ные	4,1 108	60,9	2,27	303,05		264,66	17,7	251,01	17,2	1,12
	Мука из ячменя	2,04-109	73,6	2,61	344,91	-	303,61	-	288,76	548,1	5,63
	Дрожжи кормо­вые	7,93- 10ю	83,4	3,35	340,15		304,53		291,41	650,6	6,25
	Комби­корм для свиней	8,89' 10й	93,5	1,41	352,05		317,92		305,18		8,1
	Комби­корм для птиц	3,79- 109	71,6	1,78	326,35		288,31		274,57	120,6	2,8

Глава 3, Возникновение процессов горения

Учет функции Ф(Bi) в уравнении (3.93) позволяет существенно уменьшить неточность, возникающую в результате апроксимации распре­деления температуры в горючей системе параболой второго порядка.

Рис. 3.12. Кинетические кривыеразогревов: 1-447 К; 2-450 К, 3-456; 4-458.

Для расчета критических значений температуры (T) и характерного размера (r) в уравнении (3.93) необходимы значения величин кинетиче­ских параметров: Е, Ко и v. (определение этих параметров осуществляется графоаналитическим способом по методу термического анализа из экс­периментальных кривых " - время" (Рис. 3.12).

Разработанная математическая модель позволяет рассчитывать ус­ловия самовозгорания и выполнить прогноз поведения насыпей дисперс­ной горючей массы любого размера и любой формы.

Результаты расчетов для широкого круга продуктов растительного происхождения представлены в табл. 3.2.

Данные табл. 3.2 показывают, что благодаря предложенной схеме расчета условие теплового самовозгорания можно не только установить ряд потенциальной опасности различных видов горючего дисперсного материала, но и прогнозировать критические условия их хранения (время индукции, размеры насыпи).

Необходимость обработки большого числа термических кривых де­лает описанный метод достаточно трудоемким и затрудняет его использо­вание для быстрого получения необходимой информации. В связи с этим

Корольченко А.Я. Процессы горения и взрыва ______________________

разрабоганы алгоритмы и программа для расчета критических параметров на персональной ЭВМ. Это позволяет оперативно рассчитывать критиче­ские параметры процесса самовозгорания дисперсных горючих материа­лов и осуществлять прогноз их поведения в процессе переработки, транс­портировки и хранения.

Таблица 3.3. Сравнение расчетных и экспериментальных значений температуры

Самовозгорания.

 

 

 

 

Наименование материала	Размер образца, м	Температура, °С
расчет, tp	эксперимент, tэ
Торф шатурский	0,05	128,0	139,0	11,0
Шрот хлопковый	0,05	147,0	150,0	2,5
Опилки древес­ные сосновые	0,05	166,0	170,0	3,4
Мука пшеничная (сорт высший)	0,05	173,4	178,0	4,6
Шрот соевый	0,8	57,1	59,0	1,9

Проверка точности выбранной расчетной модели условий теплового самовозгорания дисперсных горючих материалов осуществлялась на ла­бораторной и полигонной установке.

В лабораторных условиях исследовался разогрев материала с целью получения зависимости T=f(t) и определения кинетических характерис­тик. На полигонной установке изучался процесс самовозгорания в усло­виях, приближенных к реальному хранению материалов.

Результаты сопоставления расчета с экспериментом представлены в табл. 3.3, из которых следует возможность прогноза условий теплового самовозгорания по рассмотренной выше методике с достаточной для практических целей точностью.

Глава 4.

РАЗВИТИЕ ГОРЕНИЯ

4.1. Распространение пламени по газам

Д

ефлаграционное горение. Состав горючих смесей может быть раз­личным. В общем случае содержание горючего компонента может колебаться от нуля до ста процентов. Опыт показывает, что не все смеси горючего и окислителя способны распространять пламя. Распространение возможно лишь в определенном интервале концентраций. При зажигании смесей, состав которых выходит за эти пределы, реакция горения, ини­циированная зажигающим импульсом, затухает на небольшом расстоянии от места зажигания.

Для смесей горючего и окислителя, находящихся в газообразном со­стоянии, существуют минимальная и максимальная концентрации горю­чего, которые ограничивают область горючих смесей. Эти концентрации называются соответственно нижним и верхним концентрационными пре­делами распространения пламени. Вне пределов распространение пламе­ни по данной смеси невозможно.

Значения концентрационных пределов распространения пламени наиболее распространенных горючих газов приведены в табл. 5.2.

Рассмотрим причины, обуславливающие наличие предельных усло­вий распространения пламени по газовым смесям.

В начальный момент инициирования горения (искрой, накаленным телом или открытым пламенем) в горючей смеси возникает зона высокой температуры, из которой тепловой поток будет направлен в окружающее пространство. Часть тепла поступает в свежую (еще не сгоревшую) смесь, другая часть - в продукты горения. Если поток тепла в свежую смесь не­достаточен для возбуждения в ней реакции горения, первоначальный очаг пламени затухает.

Для количественной оценки этого явления рассмотрим ситуацию, ко­гда смесь горючего и окислителя движутся навстречу фронту пламени со скоростью, равной скорости распространения пламени. Тогда пламя будет неподвижным, а распределение температуры в зоне горения схематически

Корольченко А.Я. Процессы горения и взрыва

изобразится кривой, показанной на рис 4.1. Обозначим температуру газо­вой смеси вдали от пламени Т₀ а температуру продуктов горения - Т_пл.

 

Рис. 4.1. Распределение температуры в зоне горения газовой смеси

Кривую Т (Z) заменим ломаной, состоящей из прямых Т = Т₀ и Т -Тпл и касательной к кривой Т(Z) в точке перегиба.

При возникновении горения к свежей смеси по механизму тепло­проводности от единицы поверхности пламени в единицу времени подво­дится количество тепла q, определяемое соотношением:

(4.1)

где - коэффициент теплопроводности, - толщина фронта пламени.

Подведенное тепло расходуется на нагрев свежей смеси от темпера­туры Т₀ до температуры Тпл:

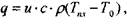(4.2)

где и - скорость потока газа, равная скорости распространения пламени, С - удельная теплоемкость, - плотность смеси.

Из соотношений (4.1) и (4.2) может быть найдена величина и:

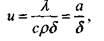
(4.3.)

Глава 4. Развитие горения

где 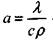- среднее значение коэффициента температуропроводности.

Поскольку скорость реакции с ростом температуры увеличивается по экспоненциальному закону, то сгорание основной массы смеси будет происходить в области, температура которой близка к максимальной Тпл. При этом зона реакции будет несколько меньше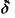

Без существенной погрешности можно принять, что ширина зоны реакции равна произведению скорости и на время пребывания смеси в зоне горения

(4.4)

а время т протекания реакции обратно пропорционально скорости реак-

то есть

(4.5)

где Е - энергия активации реакции; R - универсальная газовая постоян­ная.

Учтем, что

(4.6)

где в - безразмерный множитель, меньше единицы. Численное значение этой величины определяется видом кинетики реакции горения. Из соотношений (4.4), (4.5) и (4.6) получаем

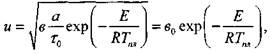
(4.7)

где в₀- величина, зависящая от свойств смеси.

Отвод тепла от зоны горения понижает температуру пламени. При этом замедляются химические процессы в пламени, и соответственно, скорость его распространения. При достаточной величине теплопотерь возникшее пламя потухает, его распространение по смеси прекращается. Определение предельных условий распространения пламени основано на

Корольченко А.Я. Процессы горения и взрыва _________________________

учете влияния тепловых потерь на температуру пламени и скорость его распространения. На этих положениях основана теория пределов распро­странения пламени, предложенная академиком Я. Б. Зельдовичем.

Согласно этой теории понижение максимальной температуры пла­мени Тпл по отношению к теоретической температуре горения Ттеор обрат­но пропорционально квадрату скорости распространения пламени:

(4.8)

где - коэффициент, характеризующий теплоотдачу.

Рис. 4.2. Пояснения к оценке критических условий распространения пламени

Совместное решение уравнений (4.7) и (4.8) позволяет оценить ско­рость распространения пламени с учетом принятых допущений. Это мож­но сделать графическим способом в прямоугольной системе координат, отложив по оси абсцисс величину Тпл, а по оси ординат - скорость распро­странения пламени. Если далее на основании уравнений (4.7) и (4.8) по­строить соответствующие кривые, то координаты точек пересечения да­дут критические значения и и Тпл.

Глава 4. Развитие горения

На рис. 4.2 кривые 1, 2 и 3 построены в соответствии с уравнением (4.8). При построении величина Т_теор принималась постоянной, а величи­ны коэффициента теплоотдачи - различными: Прямая 4 ха­рактеризует взаимосвязь между скоростью распространения и температу­рой пламени, которая задана уравнением (4.7). Как следует из графика, кривые 3 и 4 пересекаются в точках а и б. Координаты этих точек соот­ветствуют значениям и и Тпл, удовлетворяющим уравнениям (4.7) и (4.8). Точке а соответствует неустойчивый режим горения, а точке б - устойчи­вый, при котором Тпл близка к Т_теор. При увеличении теплоотвода из зоны реакции, что отражено увеличением коэффициента точки пересечения кривых будут сближаться, а значения температуры Тпл и скорости распро­странения пламени и, соответствующие устойчивому режиму горения, будут уменьшаться. При величине коэффициента 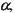отвечающем кривой 2, кривые, описывающие уравнения (4.7) и (4.8) будут иметь единствен­ную общую точку б. При дальнейшем увеличении а кривые пересекаться не будут. Это соответствует условию прекращения распространения пла­мени по смеси.

Оценим значения Тпл и и отвечающие этому условию.

В точке б производные

(4.7) и (4.8), получаем:

должны быть равны. Дифференцируя

 

 

Приравнивая правые части полученных уравнений, и решая полу­ченное соотношение относительно Т_ш, получаем:

(4.9)

или приближенно

(4.10)

Формула (4.10) свидетельствует о том, что пламя может распространять­ся по газовой смеси, если температура пламени не будет ниже теоретической

Корольченко А.Я. Процессы горения и взрыва

(т.е. температуры пламени в отсутствии теплопотерь) на величину, превы-

шаюшую

. При понижении температуры пламени на величин}'

Е ' " ' Е

оно затухает.

Решение уравнения (4.7) позволяет оценить предельную скорость распространения пламени. После преобразований получено:

(4.11)

где и_пред - предельная скорость распространения пламени, и_макс - макси­мальная, соответствующая теоретической температуре горения.

Изложенная теория объясняет наличие пределов распространения пламени по газовым смесям теплопотерями из зоны реакции. Выводы теории соответствуют экспериментально наблюдаемым фактам.

Детонация. Детонацией называется процесс превращения горючей смеси или взрывчатого вещества ВВ, сопровождающийся выделением те­плоты и распространяющийся с постоянной скоростью, превышающей скорость распространения звука в данной смеси или веществе.

В отличие от дефлаграционного горения, где распространение пла­мени обусловлено относительно медленными процессами диффузии и те­плопроводности, детонация представляет собой комплекс мощной удар­ной волны и следующей за ее фронтом зоны химического превращения. Благодаря резкому повышению температуры и давления за фронтом ударной волны химическое превращение исходных веществ в продукты горения протекает чрезвычайно быстро в очень тонком слое, непосредст­венно прилегающем к фронту ударной волны (рис. 4.3)

Рис. 4.3. Схема детонационной волны

Глава 4. Развитие горения

Ударная волна сжимает и нагревает горючую смесь (или взрывчатое вещество), вызывая химическую реакцию, продукты которой сильно рас­ширяются - происходит взрыв. Энергия, выделяющаяся в результате хи­мического превращения, поддерживает существование ударной волны, не давая ей затухать. Скорость перемещения детонационной волны постоян­на для каждой горючей смеси и взрывчатого вещества и достигает 1000-3000 м/с в газовых смесях и 8000-9000 м/с - в конденсированных взрыв­чатых веществах (табл. 4.1).

Таблица 4.1 Скорость детонации некоторых горючих смесей и взрывчатых веществ

 

Смесь или вещество	Агрегатное состояние	Плотность, г/см	Скорость детонации, м/с
2Н2+02	газ	—
СН4+202	газ	—
CS2+302	газ	-
Нитроглицерин С3Н5(ОN02)з	жидкость	1,60
Тринитротолуол (тротил) C7H5(N02)3 СНз	ТВ. В-ВО	1,62
Пентаэритритетранитрат С5Н8 (ON02)4	ТВ. В-ВО	1,77
Циклотриметилентринитроа-мин (гексоген) СзН60бМ6	ТВ. B-BO	1,80

Давление во фронте ударной волны при детонации газовых смесей дос­тигает 1-5 МПа (10-50 атм), конденсированных веществ - 10 ГПа (10³ атм).

Детонация взрывчатых веществ может инициироваться интенсив­ным механическим или тепловым воздействием (удар, искровой разряд, взрыв металлической проволочки под действием электрического тока и т.п.). Сила воздействия, необходимая для возбуждения детонации зави­сит от химической природы взрывчатого вещества или состояния го­рючей газовой смеси. К механическому воздействию чувствительны, так называемые инициирующие взрывчатые вещества (гремучая ртуть, азид свинца и др.), которые обычно входят в состав капсюлей-

Корольченко А.Я. Процессы горения и взрыва ______________________

детонаторов, используемых для возбуждения детонации вторичных (менее чувствительных) взрывчатых веществ.

В конденсированном взрывчатом веществе детонация распространяет­ся с постоянной скоростью, которая среди возможных для этого вещества скоростей распространения детонационной волны является минимальной. При этом зона химического превращения перемещается относительно ис­ходного вещества со сверхзвуковой скоростью. Вследствие этого волны раз­режения, возникающие при расширении газообразных продуктов химиче­ской реакции, не могут проникнуть в зону реакции и ослабить распростра­няющуюся впереди ударную волну. Детонация, отвечающая описанным вы­ше условиям, называется процессом Чепмена-Жуге. Соответствующая ей минимальная скорость распространения детонационной волны принимается в качестве характеристики взрывчатого вещества или горючей смеси.

Современная теория детонации позволяет рассчитывать значения ее скорости и распределение давления, плотности и температуры в детонаци­онной волне относительно продуктов реакции и скорости звука в них. Взаи­мосвязь давления и объема в распространяющейся ударной детонационной волне показана на рис. 4.4, на котором адиабата АВ соответствует ударной волне, распространяющейся в газовой смеси (р - давление, V - объем) и не вызывающей химической реакции. СД - адиабата, построенная в предполо­жении, что химическая реакция завершилась. При детонации вначале проис­ходит ударный переход 1-2 (адабатический про­цесс), затем химическая реакция переводит веще­ство из состояния 2 в со­стояние 3 по прямой, ка­сающейся адиабаты СД. Дальнейшее расширение вещества идет по адиабате СД. Скорость газовой де- Рис. 4.4. Взаимосвязь давления и объема тонации Vдет рассчитыва­в ударной волне, распространяющейся в газе ется по формуле:

(4.12)

Глава 4. Развитие горения

где q - тепловой эффект реакции, - показатель диабаты.

При определенных условиях в горючей смеси может быть возбуж­дена детонация, скорость распространения которой превышает мини­мальную скорость детонации. Например, взрыв заряда твердого взрывча­того вещества, помещенного в горючую газовую смесь, вызывает в ней ударную волну, интенсивность которой во много раз превосходит интен­сивность волны, соответствующей режиму с минимальной скоростью. В результате в газовой смеси распространяется детонационная волна с по­вышенной скоростью.

В газообразных горючих смесях распространение детонации воз­можно только при условиях, когда концентрация горючего газа (или па­ров горючей жидкости) находится в определенных пределах, зависящих от химической природы горючей смеси, давления и температуры. Напри­мер, в смеси водорода с кислородом при комнатной температуре и атмо­сферном давлении детонационная волна способна распространяться, если концентрация водорода находится в пределах от 20 до 90% об.

Переход дефлаграционного горения в детонацию. Переход де-флаграционного горения в детонацию в газовоздушных смесях возможен в следующих случаях:

• при обогащении горючей смеси кислородом;

• при очень больших размерах газовых облаков;

• при наличии турбулизаторов горения.

Согласно теории гидродинамической неустойчивости и автотурбу-лизации фронта нормального горения в горючих облаках достаточно больших размеров неизбежен переход от дефлаграционного горения к де­тонации. Экстраполяционные оценки приводят к следующим критиче­ским размерам облаков, при которых вероятность возникновения детона­ции высока: для водородовоздушных смесей - 70 м, для пропановоздуш-ных - 3500 м, для метановоздушных - 5000 м.

Турбулизация процесса горения газовых смесей с помощью различ­ных препятствий по пути распространяющегося пламени приводит к су­щественному сокращению критических размеров газовых облаков, и воз­никающая в этом случае детонационная волна становится источником возбуждения детонации в неограниченном пространстве.

Проф. В. И. Макеевым экспериментально изучена возможность перехода дефлаграции в детонацию при горении смесей СН₄ + 2(0₂ + N₂) и

2Н₂ + 0₂ + N₂ при значениях ' в интервале от 0 до 3,76 в объеме 6 м³ с

Корольченко А.Я. Процессы горения и взрыва

частично загроможденным пространством. Для загромождения использовались в различных комбинациях три тонкостенные металлические концентрически расположенные сферы-турбулизатора с большим количеством отверстий. Ко­эффициент проницаемости сфер составлял от 0,1 до 0,4, соотношение диаметров 1:2:4. Отношение объема, занятого турбулизатором к объему горючей смеси составляло от 0,01 до 0,48%. Горение инициировалось в центре сфер пережи­гаемой нихромовой проволочкой. Переход от дефлаграции к детонации наблю­дался в смесяхСН₄ +2(0₂ + N₂) при и в смесях 2Н₂ + 0₂+N₂ при < 3,2. С учетом полученных данных можно полагать, что для воздуш­ных смесей ( = 3,76) водорода и метана критический размер загроможденного пространства, при котором возможен переход к детонации, составляет примерно 1 и 10 м соответственно.

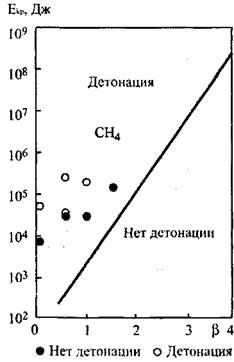
Зависимости критической энергии возбуждения детонации в загро­
можденном пространстве для исследованных смесей от состава смеси по­
казаны на рис. 4.5 и 4.6. "

 

 

Рис. 4.5. Зависимость критической Рис. 4.6. Зависимость критической
энергии возбуждения детонации энергии возбуждения детонации

от состава смеси СН₄+2(0₂+ N₂) от состава смеси 2Н₂+0₂+ N₂

Глава 4. Развитие горения

Расчет параметров детонационных волн в смесях водород-кислород-инертный газ.* Детонационные волны, образующиеся прк сгорании газовых смесей, характеризуются следующими параметрами: скоростью детонации, температурой и давлением в детонационной волне.

Для определения этих параметров проф. Ю. Н. Шебеко с сотр. предло­жен метод расчета, основанный на рассмотрении химической реакции вида:

 

В диапазоне температур примерно до 5500 К другие компоненты в продуктах реакции не образуются в существенных количествах. Введем кон­станту и, равную числу всех атомов, участвующих в химической реакции; в ходе реакции эта величина остается неизменной. Для п имеем соотношение

 

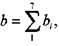
Обозначим общее число молей вещества, участвующего в химиче-

начальное число молей

ской реакции в точке равновесия, через

* При рассмотрении параметров детонационных волн приняты следующие обозначения:

давление;

плотность;

температура;

- молярная масса г-ого компонента;

скорость газа в системе скачка;

молярные теплоемкости при постоянном давлении и ооъеме соответ-

ственно;

константы, определяемые исходным составом по формулам

полная удельная энтальпия;

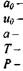
скорость звука в исходной смеси;

расчетное значение давления в детонационной волне; рассчитанное значение температуры в детонационной волне; - экспериментально измеренное значение скорости детонации; - рассчитанное значение скорости детонации.

скорость детонации; скорость звука в продуктах реакции; температура в детонационной волне; давление в детонационной волне;

Корольченко А.Я. Процессы горения и взрыва

Введем мольную долю каждого компонента 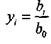, и «мольные

доли» всех атомов

Полная система уравнений для расчета детонационных адиабат со­держит четыре уравнения материального баланса по атомам (4.13)-(4.16); четыре уравнения химического равновесия (4.17)-(4.21); уравнение со­стояния (4.22); и три уравнения газодинамики: уравнение непрерывности (4.23); и два уравнения, являющиеся следствием закона сохранения плот­ности потока импульса (4.24) и энергии (4.25).

Уравнения материального баланса по атомам

(кислород) 2y₁ +уз+ у₄ + У5 = С₁у₀; (4.13)

(водород) 2у₂ + уз + 2у₄ + у₆ = с₂у₀; (4.14)

(аргон) у₇=с₃у₀;
у₁+ у₂ + уз + У₄ + У₅ + У₆+С₃У₀= 1 (4.16)

Уравнения химического равновесия

Уравнение состояния: Уравнение неразрывности:

(4.21)

(4.17) (4.18) (4.19) (4.20)

(4.22) Уравнение сохранения потока импульса:

(4.23) Уравнение сохранения энергии:

Глава 4. Развитие горения

Таким образом, система содержит 12 уравнений при 13 неизвестных (у₀-у₇) Р,р, Т, и. Чтобы замкнуть систему, необходимо дополнительное уравнение, называемое условием Чемпена-Жуге: равенство скорости газа и в системе волны и местной скорости звука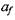

(4.25)

где у_f определяется равенством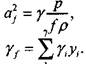

Система уравнений (4.13-4.24) позволяет сократить число перемен­ных, выразив у1-y4 через у₀ и у3-у7, а остальные переменные представив в безразмерном виде.

Состояния Чепмена-Жуге рассматриваются для начальной тем­пературы 298,15 К при начальных давлениях до 0,25 МПа. В табл. 4.1. представлены результаты расчетов: параметры состояния Чепмена-Жуге для двенадцати составов исходной смеси, при стандартных на­чальных условиях (начальное давление равно 1 атм, температура 298,15 К). В табл. 4.2. представлены рассчитанные значения темпера­туры, давления и скорости детонации для некоторых смесей. В треть­ей колонке этой таблицы даны экспериментально измеренные значе­ния скорости детонации. Рис. 4.7 иллюстрирует хорошее согласие расчетных значений с экспериментом для водородокислородной сме­си в широком диапазоне концентраций водорода, а рис. 4.8 - для гре­мучей смеси, разбавленной аргоном. Существенное возрастание ско­рости детонации, при превышении процентного содержания водорода в смеси стехиометрической отметки (67 %) объясняется уменьшением средней молярной массы смеси. Скорость фронта детонации зависит от удельного энерговыделения по закону где Q удельная эн-

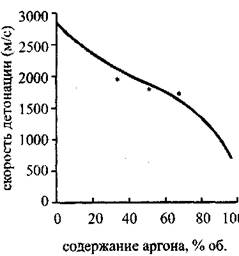
тальпия сгорания смеси, и, кроме того, от скорости звука в исходной смеси. Поэтому, даже когда молярное энерговыделение падает, ско­рость детонации растет за счет уменьшения молярной массы и увели­чения скорости звука. Согласие экспериментальных и расчетных зна­чений для смесей, содержащих инертный разбавитель (аргон), не­сколько хуже. График зависимости скорости детонации от содержа­ния аргона в смеси, состоящей из двух молей водорода и одного моля кислорода представлен на рис. 4.9. Там же отмечены точки, соответ­ствующие экспериментально измеренной скорости детонации.

Корольченко А.Я. Процессы горения и взрыва ______________________

Таблица 4.1. Результаты расчета для различных смесей водород-кислород-инертный разбавитель

 

Смеси	а0, м/с	u0 м/с	а, м/с	Т, °К	Р, атм
Но+407					10,17
Н2+302					12,18
Н2+1,502					15 72
Н2+02					16,98
1,5Н2+02					17,76
2Н2+02					18,14
зн2+о2					17,99
4Н2+02					17,44
2Н2+О2+0,1 Аr					17,91
2Н2+02+1 Аr					16,80
2Н2+02+ЗАr					15,10
2Н2+02+5 Аr					13,59

Таблица 4.2. Результаты расчета для некоторых смесей кислород-водород-инертный разбавитель в сравнении с экспериментальными данными

 

Смеси	Р расч, атм	Tрасч, К-	U0 изм, М/С	Uо расч,/С
2Н2+02	18,14
зн2+о2	17,99
4Н2+02	17,44
Н2+02	16,98
Н2+202	14,47
н2+зо2	12,18
2Н2+02+5 Аr	13,50
2Н2+02+3 Аr	15,10
2Н2+02+1,5 Аr	16,32
2Н2+02+5 Не	13,59
2Н2-O2+3 Не	15,11
2Н2+02+1,5Не	16,32		ЗОЮ

Глава 4. Развитие горения

 

 

Рис. 4.7. Зависимость скорости

детонации от содержания

водорода вкислородоводородной

смеси,

* - экспериментальные

значения

Рис. 4.8. Зависимость скорости

детонации от содержания аргона

в стехиаметрической смеси

водород-кислород-аргон:

* - экспериментально

измеренные значения

 

 

 

Рис. 4.9. Зависимость температуры

в точке ЧЖот содержания водорода

в кислородоводородной смеси

Рис. 4.10. Зависимость давления

в точке ЧЖ от содержания водорода

в кислородоводородиой смеси

Корольченко А.Я. Процессы горения и взрыва

Графики зависимости температуры и давления в точке ЧЖ от со­держания водорода в кислородоводородной смеси {рис. 4.9 и 4.10) име­ют максимум при 67% Н₂ (гремучая смесь). Эта точка отвечает мак­симальному молярному энерговыделению. Зависимость температуры от давления {рис.4.11) почти линейна, что, согласно уравнению состояния (4.21), говорит о постоянстве молярного объема в точке ЧЖ для рас­смотренных концентраций водорода в смесях при одинаковых началь­ных условиях.

Параметр , равный отношению теплоемкостей существенно меня­ется при изменении состава исходной смеси. На рис. 4.12 изображен гра­фик зависимости