 |
Марковские модели принятия решений
|
|
|
|
В данном разделе рассматриваются многостадийные задачи принятия решений с конечным числом состояний 
оптимизируемой системы S. Предполагается, что в дискретные моменты времени 
система переходит в новое состояние в соответствии с некоторой матрицей переходных вероятностей:
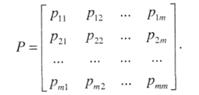
Элемент 
матрицы означает вероятность перехода системы из состояния 
, в состояние 
. Таким образом, строки матрицы соответствуют "старым", а столбцы — "новым" состояниям. Очевидно, сумма элементов любой строки матрицы равна 1.
Такой процесс поведения системы называется марковским, если вероятность перехода системы в любое возможное состояние в каждый момент времени определяется только ее состоянием в предыдущий момент времени и не зависит от более ранней предыстории.
Многие практические ситуации могут быть описаны с помощью аппарата марковских моделей. Рассмотрим конкретный пример.
Пример 4.3. Некоторая фирма занимается промышленной разработкой программного обеспечения для компьютерных систем. В начале каждого года она решает задачу замены оборудования, включающего технические и программные средства, используемые в производственном процессе и обеспечивающие необходимую технологическую среду разработки. В зависимости от результатов экспертной оценки оборудования состояние фирмы (это система S) оценивается как "хорошее" (1), "удовлетворительное" (2) и "плохое" (3). Следовательно, система может находиться в одном из трех указанных состояний. Матрица переходных вероятностей может иметь вид:
Здесь, например, число 0,3 означает, что если система находилась в "хорошем" состоянии, то в следующий момент изменения состояния (следующий момент анализа состояния фирмы) она окажется в "плохом" состоянии с данной вероятностью. В действительности изменение (ухудшение) состояния связано с процессом износа и устаревания оборудования и технологических сред. Если матрица переходных вероятностей не меняется, то достаточно просто проанализировать весь жизненный цикл системы S.
|
|
|
Предположим, что в зависимости от состояний, в которых последовательно оказывается система, может быть вычислен доход, приносимый фирмой. Логично предположить, что доход за период 
зависит от уровня оснащенности фирмы современным оборудованием и технологическим окружением, включая профессиональный уровень персонала, также требующий непрерывного повышения. В свою очередь, уровень оснащенности в значительной степени коррелирует с тем состоянием, в котором находилась фирма в начале рассматриваемого периода и в его конце. Если, например, в момент времени 
, система находилась в "хорошем" состоянии и в момент 
это состояние сохранилось, то, по-видимому, доход будет максимальным (конечно, при выполнении прочих условий, связанных с наличием заказов, ситуации на рынке и т. д.).
Для моделирования этой ситуации можно матрице переходных вероятностей 
поставить в соответствие матрицу доходов 
:
Элемент 
матрицы означает доход, полученный за период , при переходе системы из состояния 
в состояние 
. Так, число 5 означает доход, выраженный в некоторых условных единицах, при сохранении системой "удовлетворительного" состояния. Отрицательные значения отражают потери.
Имея матрицы и можно достаточно просто прогнозировать результаты функционирования системы. Ясно, что со временем оборудование устаревает и нуждается в обновлении в соответствии с новыми международными стандартами и требованиями рынка. В результате при постоянных матрицах и система может деградировать, неизменно оставаясь в плохом состоянии и принося одни убытки.
|
|
|
В реально работающих фирмах по результатам экспертного анализа проводится периодическое обновление оборудования с изменением технологического окружения и обучением персонала. Данный процесс моделируется изменением матриц переходных вероятностей и доходов. В нашем примере они, например, могут измениться следующим образом:
Здесь в матрице доходов мы учли затраты на реорганизацию и модификацию. Например, элемент 
матрицы 
оказывается меньше соответствующего элемента матрицы .
На каждом этапе мы можем принять решение не проводить модернизацию фирмы и иметь матрицы и или принять решение о необходимых изменениях и получить матрицы 
, . Возникает проблема выбора или принятия решений с целью максимизации приносимого фирмой ожидаемого (речь идет о вероятностях!) дохода. Это многоэтапная задача принятия решений, т. к. выбор осуществляется каждый раз в заданные дискретные моменты времени.
С привлечением уже рассмотренного примера обсудим основные моменты выбора оптимального решения. Предположим, что планирование стратегии поведения фирмы осуществляется на конечный период времени. Покажем, что решение может быть основано на уже известном методе динамического программирования (метод Беллмана) в соответствии с общей концепцией анализа и оптимизации многошаговых задач.
Пусть период соответствует одному году, а планирование проводится на трехлетний период. Для наглядности соответствующее дерево решений можно представить графически (рис. 4.11).
Как обычно, квадратики означают решающие вершины. Каждый квадратик соответствует определенному состоянию системы в определенный момент времени. Знак 
внутри квадрата означает, что в момент времени 
(номер этапа) система находится в состоянии 
(соответственно, "хорошее", "удовлетворительное" или "плохое" состояние). Две стрелки, исходящие из каждой "решающей" вершины, указывают на две альтернативы на каждом этапе: 
– не проводить модернизацию (это верхняя стрелка, будем называть ее стрелкой или направлением 1) или 
– проводить (это нижняя стрелка, будем называть ее стрелкой или направлением 2). Альтернативы соответствуют круглым вершинам, переход из которых осуществляется в соответствии с выбранной матрицей переходных вероятностей.
|
|
|
Следуя общему алгоритму динамического программирования, решаем задачу с конца. Двигаемся справа налево по решающим вершинам. Начнем с вершины 
. Тогда при принятии решения (без модернизации) ожидаемый доход равен
При выборе (модернизация) имеем:
Число 5,3 больше, чем 4,7, поэтому если мы окажемся в вершине , то пойдем по направлению 1, а сама вершина помечается числом 5,3. Стрелка 1 также выделяется.
Далее переходим к вершине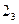 
. Получаем значения двух доходов в зависимости от принимаемых решений:
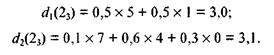
Вершина 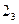помечается числом 3,1 и выделяется направление 2. Для вершины 
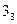получим:
Вершина 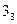помечается большим числом 0,4 и выделяется стрелка 2.
Полученные числа 5,3, 3,1, 0,4 характеризуют один акт изменения состояния и получаемый при этом локальный доход. Далее эти вычисления уже не повторяются, а значения этих локальных доходов потребуются в дальнейших расчетах.
Переходим теперь к началу второго года. Начнем с вершины 
. При выборе направления (решения) 1 имеем:
Здесь число 5,3 отражает локальный доход этапа (рассчитанный ранее), а остальные слагаемые характеризуют наилучший ожидаемый доход, получаемый на оставшихся этапах. Для второго варианта решения для этой же вершины имеем:
Теперь обратная процедура динамического программирования закончена и, двигаясь от начала дерева решений к концу, можно "прочитать" оптимальное решение. А именно: числа 10,74, 7,92, 4,23 означают оптимальный ожидаемый доход, если, соответственно, система находилась первоначально в состояниях 1, 2 и 3. Эти ожидаемые доходы достигаются, если мы всегда будем вести себя "оптимально", т. е. в соответствии с помеченными на дереве решений стрелками. В частности, в каком бы состоянии мы ни находились в начале первого года, целесообразно решение, связанное с модернизацией оборудования. То же относится к началу второго года (все выделенные стрелки направлены "вниз"). И только если в начале третьего года мы окажемся в состоянии 1, нам нецелесообразно проводить модернизацию оборудования фирмы.
|
|
|
Поставленная задача решена.
Расчетные формулы метода динамического программирования можно представить в общем виде.
Обозначим 
– общее количество этапов, а 
– оптимальный ожидаемый доход, полученный на этапах от 
до включительно при условии, что система находится в начале -го этапа в состоянии .
Обратное рекуррентное уравнение, связывающее 
и 
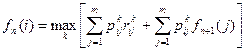можно записать в виде 
, где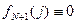 
для всех , 
– число состояний для каждого этапа, 
– номер альтернативы.
Полученное уравнение основано на том, что первая сумма представляет ожидаемый локальный доход полученный на -м этапе при выборе -й альтернативы, а вторая сумма – математическое ожидание дохода последующих этапов. Вероятность 
– есть вероятность того, что на 
этапе система окажется в состоянии в результате принятия решения .
Так как величина локального дохода не зависит от номера этапа, то его можно рассчитать лишь один раз. Введя обозначение
,
рекуррентное уравнение метода Беллмана можно записать следующим образом:
,
.
Задача с конечным числом этапов может быть обобщена в двух направлениях. Во-первых, переходные вероятности и функции дохода не обязательно должны быть одинаковы для каждого временного отрезка. Можно использовать коэффициент дисконтирования (переоценки) ожидаемых доходов для последовательных этапов, вследствие чего значения будут представлять собой приведенные величины ожидаемых доходов.
В первом случае значения доходов и переходные вероятности должны быть функциями этапа . Здесь рекуррентное уравнение приобретает вид:
,
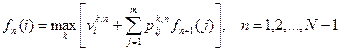, где
.
Второе обобщение заключается в следующем. Пусть (
) – годовой коэффициент переоценки (дисконтирования), тогда 
долларов будущего года равны 
долларам настоящего года. При введении коэффициента переоценки исходное рекуррентное уравнение преобразуется в следующее:
,
.
Отметим, что в теории марковских процессов принятия решений рассматриваются также модели с бесконечным числом этапов. Эти и другие вопросы рассматриваются в учебной литературе [Таха 11].
|
|
|
