 |
Выделение ассоциаций химических элементов иерархическим методом (кластер-анализ)
|
|
|
|
Лабораторная работа №4
В одном из районов выявлено месторождение золота, приуроченное к зоне развития калиевых метасоматитов, а также ряд непромышленных по масштабу проявлений золоторудной и полиметаллической минерализации.
В рудах месторождения и окружающих их ореолах рассеяния золото тесно ассоциирует с оловом и мышьяком, а на верхних горизонтах также с серебром, свинцом и сурьмой. Для окружающих неизмененных пород характерна положительная корреляционная связь между калием, ураном и торием. Непосредственно вблизи рудных тел в результате калиевого метасоматоза эта связь нарушается,
Данные особенности месторождения могут быть использованы для разбраковки многочисленных геохимических аномалий, выявленных в этом районе при проведении металлометрической съемки.
К перспективным должны быть отнесены в первую очередь комплексные геохимические аномалии с характерными для месторождения ассоциациями элементов, пространственно совпадающие с участками проявления калиевого метасоматоза.
Парные коэффициенты корреляции химических элементов по аномальным участкам приведены в табл. 1.
Таблица 1

Продолжение таблицы 1

Требуется
1) методом кластер-анализа выделить ассоциации химических элементов по одному из аномальных участков;
2) оценить перспективность данного участка, сопоставив выявленные ассоциации с ассоциациями, характерными для месторождения.
Методические указания
1. Для заданного аномального участка по данным табл. 1 составляют матрицу парных коэффициентов корреляции размерностью 9х9. Объем выборки в каждом участке — 30 значений.
2. Теснота связи различных химических элементов между собой характеризуется дистанционным показателем  , вычисляемым по формуле
, вычисляемым по формуле
|
|
|
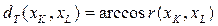 ,
,
где  - коэффициент корреляции между признаками
- коэффициент корреляции между признаками  и
и 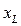 .Матрица коэффициентов корреляции трансформируется в матрицу дистанционных показателей (см. прил. 1).
.Матрица коэффициентов корреляции трансформируется в матрицу дистанционных показателей (см. прил. 1).
3. Выделение геохимических ассоциаций осуществляется путем последовательного объединения элементов в группы по мере уменьшения тесноты связи входящих в них элементов. На каждом шаге группирования рассматриваются варианты объединения элементов. В ассоциации включаются признаки или группы признаков, характеризующиеся минимальными значениями  .
.
4. Для группы признаков, объединяющей в себе несколько элементов, дистанционный показатель вычисляют как среднееиз всех дистанционных показателей в группе

где 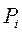 - число элементов в группе
- число элементов в группе  ,
,
По его значению может быть определен обобщенный коэффициент корреляции элементов в группе
 .
.
При объединении в одну двух групп признаков 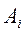 и
и  ее дистанционный показатель вычисляется как
ее дистанционный показатель вычисляется как
 где
где  - элементы, входящие в группу
- элементы, входящие в группу  ;
;  — элементы, входящие в группу
— элементы, входящие в группу  ,
,  и
и  - число элементов, входящих в группы
- число элементов, входящих в группы  и
и  .
.
5. При присоединении к ранее выделенной ассоциации одного элемента или группы элементов мерой сходства (различия) между ними служит показатель  , который вычисляется как среднее значение всех дистанционных показателей связи элементов одной группы с каждым элементом другой группы:
, который вычисляется как среднее значение всех дистанционных показателей связи элементов одной группы с каждым элементом другой группы:
 .
.
|

6. Графически характер взаимосвязи различных элементов иих ассоциаций изображается в виде дендрографа, где для ассоциаций каждого уровня группирования по горизонтальной оси откладываются показатели  , а по вертикальной - дистанционный показатель
, а по вертикальной - дистанционный показатель  (рис. 1).
(рис. 1).
7. Последовательность расчетов и формирования групп рассмотрим на примере данных по уже выявленному месторождению. В табл. 2 приведены значения парных коэффициентов корреляции (правый верхний угол) и соответствующиеим значения  (левый нижний угол).
(левый нижний угол).
|
|
|
Находим элементы, выделяемые в группу на первом шаге группирования по минимальному значению  = 0,32, которое соответствует паре Ag-Pb. Далее эти элементы рассматриваются как один признак (
= 0,32, которое соответствует паре Ag-Pb. Далее эти элементы рассматриваются как один признак ( ).
).
8. Рассчитываем значения  для вариантов объединения группы
для вариантов объединения группы  и остальных элементов. Например, показатель
и остальных элементов. Например, показатель  (
( ) вычисляется как:
) вычисляется как:
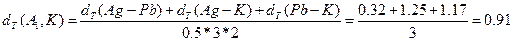
Таблица 2
|
|

Значения остальных дистанционных показателей вычисляют аналогично. Они приведены в табл. 3, где в числителе указаны суммы дистанционных показателейи их число в группе, а в знаменателе — среднее значение. Эти средние значения вводятся в матрицу размерностью 8х8. Остальные показатели заимствуют из исходной матрицы. В процессе группирования размерность матриц будет последовательно сокращаться.
9. Находим минимальное значение  в матрице размерностью 8х8. Оно равно 0,48 и характеризует группу следующего иерархического уровня
в матрице размерностью 8х8. Оно равно 0,48 и характеризует группу следующего иерархического уровня  . Вычисляем величину
. Вычисляем величину  , характеризующую связь As с группой
, характеризующую связь As с группой  :
:

10. Вычисляем значения 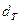 для вариантов объединения группы
для вариантов объединения группы  с другими элементами (табл. 4).
с другими элементами (табл. 4).
Эти значения выносятся в матрицу размерностью 7х7, в которой определяется минимальное значение 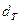 . Оно равно 0,65 и характеризует группу
. Оно равно 0,65 и характеризует группу  , объединяющую группу
, объединяющую группу  и Sn. Величина
и Sn. Величина  длягруппы
длягруппы  и Sn вычисляется как
и Sn вычисляется как

11. Вычисляем дистанционные показатели для вариантов объединения группы  с другими элементами (табл. 5).
с другими элементами (табл. 5).
Группа  выделяется по минимальному значению
выделяется по минимальному значению 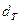 = 0,73 в матрице размерностью 6х6. Величина
= 0,73 в матрице размерностью 6х6. Величина  .
.
12. Вычисляем значения 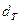 , характеризующие связь группы
, характеризующие связь группы  с другими элементами, и заносим их в матрицу размерностью 5х5 (табл. 6). Из анализа матрицы следует, что минимальное значение
с другими элементами, и заносим их в матрицу размерностью 5х5 (табл. 6). Из анализа матрицы следует, что минимальное значение 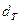 (0,81) в ней соответствует паре элементов К и Th, которые образуют группу
(0,81) в ней соответствует паре элементов К и Th, которые образуют группу  .
.
13. Формируем матрицу размерностью 4х4, для чего вычисляем дистанционные коэффициенты вариантов объединения группы  с остальными элементами и группами. Значения
с остальными элементами и группами. Значения 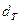 , для группы
, для группы  и отдельных элементов вычисляются так же, как и в предыдущих случаях. Для варианта объединения групп
и отдельных элементов вычисляются так же, как и в предыдущих случаях. Для варианта объединения групп  и
и  , дистанционный показатель расчитывается по формуле, приведенной в п. 4. Сумма дистанционных показателей для группы
, дистанционный показатель расчитывается по формуле, приведенной в п. 4. Сумма дистанционных показателей для группы  определена ранее (см. п. 11) и равна 7,31; для группы
определена ранее (см. п. 11) и равна 7,31; для группы  этот показатель равен 0,81. Третье слагаемое в формуле п.4 включает в себя 10 дистанционных показателей (К-Аg, К-Рb, K-As, К-Sn, К-Аu, Тh-Аg, Тh-Рb, Тh-Аs, Тh-Sn, Тh-Аu), сумма которых равна 11,16. Таким образом, величина (
этот показатель равен 0,81. Третье слагаемое в формуле п.4 включает в себя 10 дистанционных показателей (К-Аg, К-Рb, K-As, К-Sn, К-Аu, Тh-Аg, Тh-Рb, Тh-Аs, Тh-Sn, Тh-Аu), сумма которых равна 11,16. Таким образом, величина ( ) определится как
) определится как
|
|
|

Минимальным в данной матрице будет значение 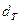 = 0,87, по которому выделена группа
= 0,87, по которому выделена группа  . Величина
. Величина  равна 5,67/5=1,13.
равна 5,67/5=1,13.
Таблица 5
|

14. Вычисляем дистанционные показатели для матрицы размерностью 3х3. Вариант объединения групп  и
и  характеризуется дистанционным показателем
характеризуется дистанционным показателем

Для группы К-Тh, U величина 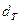 равна 1,15; для группы
равна 1,15; для группы  показатель
показатель 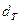 равен 0,99. Таким образом, в группу
равен 0,99. Таким образом, в группу  объединяются все элементы, кроме U. Показатель
объединяются все элементы, кроме U. Показатель  для групп
для групп  и
и  равен 13,36/12 = 1,11.
равен 13,36/12 = 1,11.
15. Последняя группа объединяет все элементы, ее дистанционный показатель равен 1,05. Величина  равна 1,31.
равна 1,31.
16. Предельное значение коэффициента корреляции для доверительной вероятности 0,95 при данном объеме выборки составляет 0,42. Ему соответствует значение 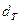 = 1,13. Таким образом, связь ассоциации элементов Аg—Рb—Аs—Sn—Аu—Sb—К—Тh с ураном может считаться не значимой.
= 1,13. Таким образом, связь ассоциации элементов Аg—Рb—Аs—Sn—Аu—Sb—К—Тh с ураном может считаться не значимой.
17. Графическое изображение выявленных ассоциаций иих взаимосвязей приведено на рис. 4. Для ассоциаций каждого иерархического уровня по вертикали откладываются значения 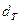 или соответствующие им величины коэффициентов корреляции r; по горизонтали в выбранном масштабе отрезками, соединяющими элементы или группы, указываются значения
или соответствующие им величины коэффициентов корреляции r; по горизонтали в выбранном масштабе отрезками, соединяющими элементы или группы, указываются значения  . Для групп, состоящих из двух элементов, величины
. Для групп, состоящих из двух элементов, величины  и
и 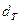 равны.
равны.
Анализ данного дендрографа показывает, что наиболее сильными внутренними связями обладают ассоциации рудообразующих элементов Аg-Рb—As—Sn—Аu—Sb, а также ассоциация К—Тh. Относительно высокая связь золота как с оловом и мышьяком, так и с серебром, свинцом и сурьмой позволяет говорить о довольно неглубоком уровне эрозионного среза. Наличие корреляционной связи между рудными элементами и калием указывает на проявление процессов калиевого метасоматоза на объекте; об этом же свидетельствует отсутствие корреляционной связи с ураном тория и калия. Относительно невысокая теснота связи между рудными элементами, торием и калием объясняется более широким развитием ореолов измененных пород в сравнении с ореолами рудных элементов.
|
|
|
|
|
|


