Задание 1. Исследование связей между двумя исследуемыми признаками.

Лабораторная работа №1. Технологии статистических расчетов в MS EXCEL.

 

Цель: научиться использовать возможности MS Excel для проведения статистических расчетов.

Задачи:

1. Расчет коэффициента корреляции Пирсона и t-статистики Стьюдента.

2. Построение модели регрессии различными способами.

3. Выбор наиболее точной модели связи между двумя величинами.

Параметрический корреляционный анализ.

Одна из наиболее распространенных задач статистического исследования состоит в изучении связи между выборками. Обычно связь между выборками носит не функциональный, а вероятност­ный (или стохастический) характер. В этом случае нет строгой, однозначной зависимости между величинами. При изучении стохастических зависимостей разли­чают корреляцию и регрессию.

Корреляционный анализ состоит в определении степени связи между двумя слу­чайными величинами X и Y. В качестве меры такой связи используется коэффи­циент корреляции. Коэффициент корреляции оценивается по выборке объема п связанных пар наблюдений (x_i, y_i) из совместной генеральной совокупности X и Y. Существует несколько типов коэффициентов корреляции, применение которых зависит от измерения (способа шкалирования) величин X и Y.

Для оценки степени взаимосвязи величин X и Y, измеренных в количественных шкалах, используется коэффи­циент линейной корреляции (коэффициент Пирсона), предполагающий, что выборки X и Y распределены по нормальному закону.

1. Линейный коэффициент корреляции — параметр, который характеризует степень линей­ной взаимосвязи между двумя выборками, рассчитывается по формуле:

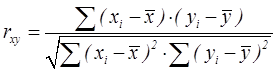
где х_i — значения, принимаемые в выборке X,

y_i — значения, принимаемые в выборке Y;

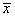— средняя по X, 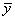— средняя по Y.

 

Коэффициент корреляции изменяется от -1 до 1. Когда при расчете получается величина большая +1 или меньшая -1 — следовательно, произошла ошибка в вычислениях. При значении 0 линейной зависимости между двумя вы­борками нет.

Знак коэффициента корреляции очень важен для интерпре­тации полученной связи. Если знак ко­эффициента линейной корреляции — плюс, то связь между кор­релирующими признаками такова, что большей величине одного признака (переменной) соответствует большая величина дру­гого признака (другой переменной). Иными словами, если один показатель (переменная) увеличивается, то соответственно уве­личивается и другой показатель (переменная). Такая зависимость носит название прямо пропорциональной зависимости.

Если же получен знак минус, то большей величине одного признака соответствует меньшая величина другого. Иначе гово­ря, при наличии знака минус, увеличению одной переменной (признака, значения) соответствует уменьшение другой пере­менной. Такая зависимость носит название обратно пропорцио­нальной зависимости.

Теснота связи и величина коэффициента корреляции.

Коэффициент корреляции rxy	Теснота связи
+ 0,91-1,0	Очень сильная
+ 0,81-0,9	Весьма сильная
+ 0,65-0,8	Сильная
+ 0,45-0,64	Умеренная
+ 0,25-0,44	Слабая
До + 0,25	Очень слабая
«+» - прямая зависимость «-» - обратная зависимость

T-статистика Стьюдента.

Для того чтобы оценить наличие связи между двумя переменными, также можно использовать t-статистику Стьюдента, которая оценивает отношение величины линейного коэффициента корреляции к среднему квадратическому отклонению и рассчитывается по формуле

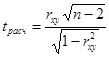
Полученную величину t_расч сравнивают с табличным значением t-критерия Стьюдента с n-2 степенями свободы. Если t_расч > t_табл, то практически невероятно, что найденное значение обусловлено только случайными совпадениями величин X и Y d в выборке из генеральной совокупности, т.е. существует зависимость между X и Y. И наоборот, если t_расч < t_табл , то величины X и Y независимы.

 

Регрессионный анализ.

Цель регрессионного анализа – определить количественные связи между зависимыми случайными величинами. Одна из этих величин полагается зависимой и называется откликом, другие – независимые, называются факторами. Для установления степени зависимости между откликом и факторами используются вычисляемые величины ковариации и коэффициент корреляции. Если коэффициент корреляции по абсолютной величине близок к единице, то для построения зависимости используется линейная модель. Для других случаев используются более сложные нелинейные модели.

Уравнение линейной регрессии имеет вид:

Y=a₁X₁ + a₂X₂ + …+ a_kX_{k ,} где а₁, а₂… а_{k –} параметры, подлежащие определению методом наименьших квадратов (МНК). В среде MS Excel для этого используется встроенная функция ЛИНЕЙН и инструмент Регрессия из Пакета анализа.

Задание 1. Исследование связей между двумя исследуемыми признаками.

Условие задачи: По 20 туристическим фирмам были установлены затраты на рекламную кампанию и количество туристов, воспользовавшихся после ее проведения услугами каждой фирмы. Определить коэффициент корреляции между исследуемыми признаками.

Ход выполнения:

1. Откройте новую книгу MS Excel и создайте таблицу согласно рис. 1:

Рис.1.

2. Рассчитайте в ячейке С23 коэффициент корреляции, используя функцию КОРРЕЛ из категории Статистические. Синтаксис функции:

КОРРЕЛ (массив1; массив 2):

где массив1 – ссылка на диапазон ячеек первой выборки (X);

массив2 – ссылка на диапазон ячеек второй выборки (Y).

В нашей задаче формула будет иметь вид: =КОРРЕЛ(B2:B21;C2:C21)

3. Сделайте вывод о тесноте связи между затратами на рекламу и количеством привлеченных туристов.

4. Оцените значимость коэффициента корреляции. С этой целью рассматриваются две гипотезы. Основная Н₀: r_xy=0 и альтернативная Н₁: r_xy≠0. Для проверки гипотезы Н₀ рассчитайте t-статистику Стьюдента по формуле, указанной выше в ячейке С24. В нашем случае число степеней свободы ν = n-2=20-2 = 18 и формула будет следующей: =C23*КОРЕНЬ(20-2)/КОРЕНЬ(1-(C23*C23))

5. Сравните полученное значение с критическим значением t_ν,α распределения Стьюдента. (При ν =18 и доверительной вероятности α = 0,05, t_{ν,α,табл} = 1,734). Сделайте вывод о наличии связи между исследуемыми величинами.

 

123Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: