 |
Статистика личного страхования
|
|
|
|
СОДЕРЖАНИЕ
1. СТАТИСТИКА СТРАХОВАНИЯ
1.1 Основные понятия статистики страхования
1.2 Статистика имущественного страхования
1.2.1 Основные абсолютные и относительные показатели
1.2.2 Расчет нетто-ставки
1.3 Статистика личного страхования
2. ПРАКТИЧЕСКОЕ ЗАДАНИЕ
ВЫВОДЫ
СПИСОК ЛИТЕРАТУРЫ
СТАТИСТИКА СТРАХОВАНИЯ
Основные понятия статистики страхования
Страхование представляет систему экономических отношений по защите имущественных и неимущественных интересов юридических и физических лиц путём формирования денежных фондов, предназначенных для возмещения ущерба и выплаты страховых сумм при наступлении страховых событий.
Страховое событие – потенциальный страховой случай, на предмет которого производится страхование (несчастный случай, болезнь и т.п.).
Страховой случай – это свершившееся страховое событие, с наступлением которого возникает обязанность страховщика произвести оплату страхователю.
При страховом случае с личностью страхователя выплата называется страховым обеспечением, а при страховом случае с имуществом - страховым возмещением.
Статистика имущественного страхования
Стихийные бедствия, их последствия и несчастные случаи нельзя предусмотреть в буквальном смысле. Закономерность этих событий можно проследить только в результате изучения массовой статистической информации, применяя соответствующие методы, основанные на теории вероятностей.
Основные абсолютные и относительные показатели
Основу системы показателей составляют характеристики, получаемые непосредственно из наблюдения. Применяемые в имущественном страховании показатели делятся на 3 группы: объёмные показатели, средние и относительные.
|
|
|
Основные абсолютные показатели
| · Страховое поле, максимальное число объектов, которое может быть охвачено страхованием | Nmax |
| · Число застрахованных объектов, или число заключённых договоров страхования за определенный период(страховой портфель) | N |
| · Страховая сумма застрахованного объекта | S |
| · Сумма поступившего страхового платежа (страховой взнос) | V |
| · Число страховых случаев | 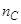
|
| · Число пострадавших объектов | 
|
| · Страховая сумма пострадавших объектов | 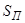
|
| · Сумма выплаченного страхового возмещения | W |
Таблица 1.1. Основные относительные показатели имущественного страхования
| Показатель | Формула расчета | Пояснения |
| Степень охвата страхового поля | 
| Показывает долю застрахованных объектов от числа максимально возможных. Характеризует уровень развития добровольного страхования |
| Страховой платеж на 1 руб. страховой суммы | 
| Характеризует тарифную ставку страхования |
| Частота страховых случаев | 
| Показывает, сколько страховых случаев приходится в расчёте на 100 или 1000 застрахованных объектов. Можно интерпретировать как вероятность гибели или повреждения застрахованного имущества. Всегда < 1. |
| Уровень опустошительности страхового случая (коэф-фициент кумуляции риска) | 
| Показывает, сколько объектов пострадало в одном страховом случае |
| Доля пострадавших объек-тов из числа застрахованных | 
| |
| Коэффициент выплат страхового возмещения (норма убыточности) | 
| Показывает, сколько копеек выплачивается в качестве страхового возмещения с каждого рубля страхового платежа. Если величина этого показателя >1, то страхование имущества убыточно. В динамике этот показатель должен уменьшаться. |
| Полнота уничтожения пострадавших объектов (коэффициент ущербности) | 
| Характеризует удельный вес суммы возмещения в страховой сумме пострадавших объектов. Если показатель равен 1, значит, в результате страхового случая ущерб равен действительной стоимости застрахованного имущества. Та-кой ущерб называется полным ущербом. Если  <1, ущерб называется частичным. <1, ущерб называется частичным.
|
| Уровень убыточности страховых сумм | 
| Показывает, сколько рублей возмещается на каждый рубль страховой суммы |
|
|
|
Уровень убыточности страховых сумм - важнейший показатель имущественного страхования. Он зависит от:
· количества заключённых договоров, N,
· страховой суммы застрахованных объектов, S,
· числа пострадавших объектов,  ,
,
· полноты уничтожения застрахованных объектов,  ,
,
· суммы выплат страхового возмещения, W.
Таким образом, он является результатом взаимодействия пяти из семи основных объемных показателей.
Таблица 1.2 Средние показатели по совокупности объектов используются для изучения производственной и хозяйственной деятельности страховых организаций:
| Показатель | Формула расчета | Пояснения |
| Средняя страховая сумма застрахованного имущества |  
| |
| Средний размер страхового взноса | 
| |
| Среднее страховое возме-щение (средняя сумма страховых выплат) | 
| |
| Средний уровень убыточ-ности страховых сумм | 
| Показатель должен быть < 1, т.к. иначе это означало бы недострахование. |
| Коэффициент тяжести страховых событий | 
| Показывает, какая часть страховой суммы уничтожена |
| Средняя страховая сумма пострадавших объектов | 
| |
| Средний показатель полно-ты уничтожения объектов (коэффициент ущербности) | 
|  1 означает, что объек-ты полностью уничтожены. 1 означает, что объек-ты полностью уничтожены.
|
По данным текущей отчетности страховых компаний непосредственно исчислить можно лишь некоторые из перечисленных показателей (долю пострадавших объектов, показатель выплат страхового возмещения, уровень взносов по отношению к страховой сумме, показатель убыточности, а также средние величины). Для исчисления других показателей необходимо проведение специального статистического наблюдения, привлечение отчетности других организаций и ведомств (например, при исчислении показателя охвата страхового поля) или применение соответствующих статистических методов для возмещения неполноты учета.
|
|
|
Динамику среднего уровня убыточности можно изучать с помощью системы взаимосвязанных индексов переменного и постоянного состава, структурных сдвигов:
 ,
,
 ,
,
где  - доля (удельный вес) страховой суммы отдельных видов имущества в общей страховой сумме
- доля (удельный вес) страховой суммы отдельных видов имущества в общей страховой сумме
Расчет нетто-ставки
Одной из задач статистики в области страхования является обоснование уровня тарифной ставки.
Тарифная ставка – ставка страхового платежа предназначена для возмещения ущерба, причинённого застрахованному имуществу страховым событием, а также для других расходов страховых организаций.
Тарифная ставка, которую называют брутто-ставкой, U, состоит из двух частей:
· нетто-ставки, U', которая составляет 90-91 % от брутто-ставки,
· и нагрузки (надбавки). Нагрузка устанавливается в % к брутто – ставке, обычно составляет 9-11 % от нее.
U=U' + U  ,
,
где f – доля нагрузки в брутто-ставке.
Брутто-ставка рассчитывается по формуле:

Нетто-ставка, U', составляет основную часть тарифа (ставки страхового платежа) и предназначена для создания фонда на выплату страхового возмещения. Обеспечивает возмещение убытков страхователей.
Нагрузка (надбавка) к нетто-ставке служит для образования резервных фондов содержания страховых органов, финансирования превентивных (предупреждение появления страховых событий) и репрессивных мероприятий (ликвидация наступивших последствий).
В основу расчёта нетто – ставки, U', положен уровень убыточности имущества. Средний показатель убыточности рассчитывается по отчетным данным об убыточности за ряд лет:
 = S q / n,
= S q / n,
где n - число лет,
или на основании данных о размерах страховых возмещений и о страховых суммах:
 .
.
Затем рассчитывается среднее квадратическое отклонение уровня убыточности от среднего значения:

Для того, чтобы нетто-ставка отражала наиболее вероятную величину, к ней добавляется среднее квадратическое отклонение, умноженное на коэффициент доверительной вероятности. Таким образом, расчёт нетто-ставки производят по формуле:
|
|
|
U' =  + t s,
+ t s,
где t - коэффициент доверия в соответствии с принятой вероятностью наступления страховых событий (коэффициент Лапласа).
Статистика личного страхования
Расчеты в личном страховании основаны на таблицах смертности и средней продолжительности жизни населения и показателях доходности.
В таблице смертности используются одногодичные возрастные группы от 0 (новорожденные) до 100 лет.
Таблица 1.3. Макет таблицы смертности и средней продолжительности жизни
| Возраст, лет | Число доживающих до возраста X лет | Число умирающих при переходе от возраста X к возрасту X+1 | Вероятность умереть в возрасте от X до X+1 год | Вероятность дожить до возраста X+1 |
| X | LX | dX | 
| 
|
| X+1 |
Вероятность умереть в течение предстоящего года жизни, т.е. при переходе от возраста X к возрасту X+1 рассчитывается:

Вероятность дожить до следующего возраста можно определить как

Средний показатель доходности за период рассчитывается по стране в целом или как средняя арифметическая взвешенная по доходам от инвестиций конкретной страховой компании за предыдущие периоды:
 ,
,
где i – доходность по отдельному виду инвестиций, в долях от 1,
f – объем инвестиций,
n – число инвестиционных проектов.
Расчет нетто-ставки при страховании лица в возрасте Х лет на дожитие n лет:
 ,
,
где  - число лиц в начале срока страхования (из таблицы смертности),
- число лиц в начале срока страхования (из таблицы смертности),
 - число лиц, доживших до конца срока страхования (из таблицы смертности),
- число лиц, доживших до конца срока страхования (из таблицы смертности),
 - средняя доходность за период действия договора,
- средняя доходность за период действия договора,
FV –сумма страхового обеспечения,
n – срок договора страхования.
ПРАКТИЧЕСКОЕ ЗАДАНИЕ
Исходные данные
Таблица 2.1. Показатели деятельности предприятия за отчётный период
| № предприятия | Объём производства, тонн | Среднегодовая стоимость основных производственных фондов, млн. руб. |
| А | 1 | 2 |
| 1 | 978 | 3,52 |
| 2 | 1043,6 | 3,71 |
| 3 | 620,6 | 2,13 |
| 4 | 485,1 | 1,05 |
| 5 | 884,5 | 2,82 |
| 6 | 1020,4 | 4,1 |
| 7 | 872,3 | 2,73 |
| 8 | 421,8 | 1,5 |
| 9 | 280,6 | 0,89 |
| 10 | 851,8 | 3,04 |
| 11 | 637,2 | 2,37 |
| 12 | 815,6 | 2,56 |
| 13 | 921,7 | 3,2 |
| 14 | 544,3 | 1,64 |
| 15 | 915,1 | 3 |
| 16 | 1010,4 | 3,61 |
1. Для того, чтобы провести аналитическую группировку с равными интервалами, необходимо определить оптимальное число групп, которое рассчитывается по формуле Стержесса:
m=1+3,321·lgN, (1)
где m – число групп, N – число единиц совокупности.
m=1+3,321·lg16=4,999.
Так как число групп должно быть целым, то выбираем m=5.
2. В качестве признака, по которому строится группировка, берётся факторный признак х – объём производства, от которого зависит результативный признак у – среднегодовая стоимость основных производственных фондов.
|
|
|
Зная число групп, рассчитываем величину интервала:
 (2)
(2)
Величина интервала составляет:

Таблица 2.2. Вспомогательная таблица для построения группировки предприятий по объёму производства
| № группы | Группы предприятий по объёму производства, тонн | Номера предприятий, входящих в группу |
| 1 | 280,6 – 433,2 | 8, 9 |
| 2 | 433,2 – 585,8 | 4, 14 |
| 3 | 585,8 – 738,4 | 3, 11 |
| 4 | 738,4 – 891 | 5, 7, 10, 12 |
| 5 | 891 – 1043,6 | 1, 2, 6, 13, 15, 16 |
На основании вспомогательной таблицы (таблица 2) и таблицы исходных данных (таблица 1), построим аналитическую группировку и представим её в статистической таблице (таблица 3).
Таблица 2.3. Аналитическая группировка предприятий по объёму производства для выявления взаимосвязи между показателями: объём производства и среднегодовой стоимости основных производственных фондов
| Группы предприятий по объёму производства, тонн | Количество предприятий, ед. | Удельный вес Группы предприятий, % | Объём производства, тонн | Среднегодовая стоимость основных производственных фондов, млн. руб. | |||
| итого | в среднем | итого | в среднем | ||||
| А | 1 | 2 | 3 | 4 | 5 | 6 | |
| 280,6 – 433,2 | 2 | 12,5 | 702,4 | 351,2 | 2,39 | 1,195 | |
| 433,2 – 585,8 | 2 | 12,5 | 1029,4 | 514,7 | 2,69 | 1,345 | |
| 585,8 – 738,4 | 2 | 12,5 | 1257,8 | 628,9 | 4,5 | 2,25 | |
| 738,4 – 891 | 4 | 25 | 3424,2 | 856,05 | 11,15 | 2,788 | |
| 891 – 1043,6 | 6 | 37,5 | 5889,2 | 981,53 | 21,14 | 3,523 | |
| Итого: | 16 | ||||||
100
12303
41,87
В среднем:
768,94
2,617


 , (3)
, (3)

 , (4)
, (4)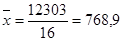 тонн
тонн , (5)
, (5) – среднее значение i-ой группы, m – число групп.
– среднее значение i-ой группы, m – число групп.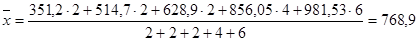 тонн
тонн , (6)
, (6) ,
,  – соответственно максимальное и минимальное значение признака.
– соответственно максимальное и минимальное значение признака. (7)
(7) (8)
(8) (9)
(9) (10)
(10)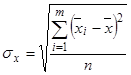 (11)
(11) (12)
(12) ,
, ,
, ,
, ,
,
 ,
,

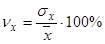 , (13)
, (13) %
% измеряет вариацию результативного признака по всей совокупности под влиянием всех факторов, обусловивших эту вариацию. Данный вид дисперсии рассчитывается на основании исходных несгруппированных данных по формуле:
измеряет вариацию результативного признака по всей совокупности под влиянием всех факторов, обусловивших эту вариацию. Данный вид дисперсии рассчитывается на основании исходных несгруппированных данных по формуле: , (14)
, (14) ,
, , млн. руб.
, млн. руб. ,
, (млн. руб)
(млн. руб)  характеризует систематическую вариацию под воздействие признака – фактора, положенного в основание группировки. Она является мерой вариации частных средних по группам
характеризует систематическую вариацию под воздействие признака – фактора, положенного в основание группировки. Она является мерой вариации частных средних по группам  и определяется по формуле:
и определяется по формуле: (15)
(15) ,
, ,
, , млн. руб.
, млн. руб. ,
,
 ,
,

 :
: , (16)
, (16) определяется путём суммирования отдельных внутригрупповых дисперсий, взвешенных по частоте.
определяется путём суммирования отдельных внутригрупповых дисперсий, взвешенных по частоте. , (17)
, (17) , млн. руб.
, млн. руб. ,
,
 ,
,
 ,
, (млн. руб.)
(млн. руб.)  (18)
(18) :
: , (19)
, (19)
 (20)
(20)
 >0,7, связь между признаками объём реализации и среднегодовая стоимость основных производственных фондов – сильная.
>0,7, связь между признаками объём реализации и среднегодовая стоимость основных производственных фондов – сильная. ), i =1,... N.
), i =1,... N.