 |
Пользовательский интерфейс
|
|
|
|
Лабораторная работа №2
Цель: получить навыки реализации решения физических задач в среде Visual C++ 6.0.
Задачи:
1) сформулировать требования;
2) разработать алгоритм решения задачи;
3) синтезировать пользователький интерфейс;
4) реализовать на основании алгоритма программный код.
Постановка задачи
Рассмотрим процесс изотермического всплытия пузырька газа.
С глубины h 0 = 10 м в воде начал всплывать пузырек идеального газа, имевший в начале пути радиус r 0 = 5 мм. Как будет меняться по мере всплытия радиус пузырька? Атмосферное давление – нормальное, изменением температуры воды t в зависимости от глубины h пренебречь.
Итак, нам необходимо разработать программу расчета радиуса пузырька.
Сформулируем требования к программе.
1) Необходимо синтезировать модель процесса всплытия пузырька.
2) Интерфейс программы необходимо реализовать на основе диалогового окна.
3) Структура интерфейса должна соответствовать рис. 34. Интерфейс должен позволять пользователю вводить начальные данные r 0 и h 0.
4) При нажатии на кнопку «Расчет» должен моделироваться процесс всплытия пузырька с шагом по лубине равным 0.25 м. Каждая итерация должна записываться в текстовый файл в виде пары чисел глубина — радиус. В поле Метка2 должен выводиться конечный радиус пузырька на момент всплытия выраженный в мм. Поле Метка1 должно быть пустым.
4) При нажатии на кнопку «Визуал» должен визуализироваться процесс изменения радиуса пузырька записанный в текстовом файле при нажатии кнопки «Расчет». Визуализация заключается в выводе текущих глубины и радиуса в виде текста, а также в отрисовке радиуса в виде некоего графика. В поле Метка1 должна выводится текущая глубина в м, а в поле Метка2 текущий радиус в мм. Между каждой итерацией необходимо делать паузу — 300 мс.
|
|
|
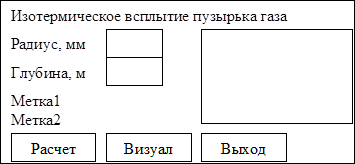
Рис. 34.
Модель процесса
Для синтеза модели процесса прежде всего необходимо рассмотреть физику процесса.
Для идеального газа справедливо уравнение состояния:
, (1)
где p – давление, Па;
V – объем, м3;
m – масса, кг;
R – универсальная газовая постоянная, R ≈ 8,31 кДж/(кмоль·К);
T – температура, К;
μ – молярная масса, кг/моль.
По условию задачи, в процессе всплытия пузырька идеального газа постоянны такие величины: масса m и температура T пузырька.
Тогда величина m·R·T / μ, то есть правая часть выражения (1), также постоянна и не меняется в процессе всплытия. Отсюда справедливо:
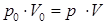, (2)
где p 0, V 0 – параметры газа в начале всплытия;
p, V – параметры газа в любой другой момент времени.
Из (2) получаем объем пузырька V (h) как функцию от глубины h:
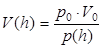(3)
Рассмотрим величины, входящие в правую часть выражения (3). Величины p 0, V 0 рассчитываются на основе исходных данных. В самом деле, для p 0 справедливо:
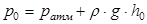, (4)
где pатм = 1,01·105 Па (нормальное атмосферное давление);
ρ = 1000 кг/м3 (плотность воды);
g = 9,81 м/с2 (ускорение свободного падения);
h 0 = 10 м (глубина начала всплытия пузырька по условию задачи).
После подстановки констант в (4) получаем для p 0:
p 0 = 1,01·105 + 1000·9,81·10 ≈ 1,99·105 (Па)
В начале всплытия для объема газового пузырька V 0 справедливо:
, (5)
где π ≈ 3,14;
r 0 = 5 мм.
После подстановки констант в (5) получаем для V 0:
V 0 = 1,33·3,14·(5·10-3)3 ≈ 5,22 · 10-7(м3)
По аналогии с (4) для p (h) справедливо:
, (6)
Подставив константы в (6), для p (h) получится:
p (h) = 1, 01·105 + 1000·9,81· h = (1, 01 + 9,81·10-2 · h) ·105 (Па) (7)
Таким образом, мы уже имеем выражения для всех величин, входящих в (3).
С учетом p 0, V 0 и (7) из (3) следует:
|
|
|
(м3). (8)
Кроме того, для V (h) справедливо:
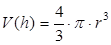(9)
Из (9) получаем выражение для r:
(10)
Подставив (8) в (10), получим окончательное выражение для радиуса всплывающего с глубины 10 м. газового пузырька, как функции от глубины r (h):
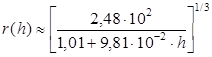(мм). (11)
Из (11) видно, что по мере уменьшения h (всплытия пузырька) радиус газового пузырька будет расти. Пузырек будет иметь максимальный радиус r max на поверхности, т.е. при h = 0:
r max = r (0) ≈ 6,26 (мм)
Можно резюмировать, что мы имеем простое выражение (11), описывающее изменение радиуса пузырька идеального газа при изотермическом всплытии в воде с глубины 10 метров. Согласно (11) в начале всплытия (h 0 = 10 м) радиус пузырька был 5 мм. К моменту всплытия он составит примерно 6, 26 мм. Это увеличение радиуса пузырька на 25,2 % не так уж и мало. Так как объем пузырька пропорционален кубу радиусу пузырька, при увеличении радиуса пузырька в 1, 252 раз объем пузырька увеличится в 1,96 раз, т.е. почти в 2 раза.
Чтобы записать выражение для r (h) в общем виде, подставим в (3) выражения (4), (5), (6).
Это даст соотношение для V (h):
(12)
Учтем также, что для V (h) есть выражение (9).
Приравнивая правые части (9) и (12), получаем соотношение для r (h):
. (13)
Итак, в результате математических выкладок мы получили простое выражение (13) для расчета требуемой величины r (h). Студенты могут спросить зачем потребовалось так глубоко описывать всю физику процесса? Почему нельзя было сразу привести формулу (13) и в дальнейшем работать только с ней?
В лабораторном практикуме первого семестра мы затрагивали вопросы самодиагностирования функций и программ. Наличие подробного математического обеспечения позволяет более качественно подойти к вопросу самодиагностики и проектирования ПО в целом.
Современная технология разработки ПО требует наличия подробного математического описаная решения реализуемой задачи. Оно позволяет, прежде всего, убедится на ранних этапах проектирования ПО в том, что алгоритмы ПО соответствуют требованиям заказчика. Кроме того, подробное математическое описание позволяет программисту понять физику задачи и подходить к процессу ее реализации в программном коде с понимаем того, что он делает. Вероятность допустить при этом ошибку существенно снижается.
|
|
|
Для примера рассмотрим такую ситуацию. Вы написали программу расчета некой величины А. Если вы ничего не знаете о физической сущности этой величины, то вы не в состоянии проконтролировать правильность расчета. Если же вам известно из матописания, что А есть количество чего-либо, то получив отрицательный результат вы можете определить, что либо в расчете либо в исходных данных возникла ощибка.
Пользовательский интерфейс
Теперь рассмотрим, как можно программно реализовать решение физической задачи об изотермически всплывающем в воде пузырьке идеального газа с помощью среды Visual C++ 6.0.
Создадим визуальный интерфейс на основе диалогового окна.
Для начала запустите среду программирования Visual C++ 6.0.
В пункте меню File укажите: New \ Projects \ MFC AppWizard (exe) (рис. 35).
В окне Project name укажите имя вашего проекта: Control Elements.
В окне Location укажите путь, по которому будет храниться ваш проект, например, D:\ Temp \ ControlElements.
Нажмите кнопку OK.
В первом окне (Step1) укажите тип вашего приложения Dialog based (здесь мы определяем, что в основе нашего приложения будет лежать диалоговое окно) и нажмите кнопку Finish (рис. 36). В появившемся итоговом окне (рис. 37) также нажмите ОК.
Рис. 35.
Рис. 36 Рис. 37
Для формирования пользовательского интерфейса воспользуйтесь материалом изложенным в лабораторной работе №1.
Напомним, что язык интерфейса по умолчанию устанавливается на английский. Если вы желаете использовать в интерфейсе русский язык, то в свойствах диалога необходимо внести соответствующие изменения.
Далее необходимо сделать следующее.
1. Уберите все элементы с лица новой формы.
2. Используя средства редактора, создайте облик диалога, как показано на рис. 38.
Рис. 38
Задайте идентификаторы для всех элементов диалога. Заголовок и подписи слева являются элементами Static Text. Их идентификаторы по умолчанию (IDC_STATIC) не меняйте. Элементы Static, слева внизу, также являются Static Text. Присвойте верхнему элементу индентификатор IDC_H, а нижнему IDC_R. В дальнейшем мы будем использовать их для вывода текущего значения глубины и радиуса пузырька. Элементы ввода справа от Static Text есть Edit Box. Верхнему задайте индентификатор IDC_EDIT_BEGIN_R, а нижнему — IDC_EDIT_BEGIN_H. Прямоугольник в правой части формы есть элемент Picture. Позднее мы используем только пустую рамку этого элемента. Такой прием называется созданием местодержателя (place holder). Держатель места обязательно должен быть идентифицирован (задайте IDC_DRAW_AREA), иначе потом невозможно будет его использовать. Кнопкам в порядке слева направо задайте идентификаторы IDC_BTN_CALC, IDC_BTN_SHOW и IDC_BTN_EXIT.
|
|
|
Для упрощения операций ввода/вывода свяжем с некоторыми элементами управления определенные переменные рис. 39.
С элементом IDC_EDIT_BEGIN_R свяжите вещественную переменную m_R0. Мы будем использовать ее для получения начального радиуса пузырька. С элементом IDC_EDIT_BEGIN_H свяжите вещественную переменную m_H0. Ее мы будем использовать для получения начальной глубины пузырька.
Для вывода текущих глубины и радиуса пузырька свяжите с элементом IDC_R переменную m_CurR типа CString, а с элементом IDC_H переменную m_CurH тоже типа CString.
Рис. 39
Итак, у нас готов визуальный пользовательский интерфейс. Осталось только создать заготовки обработчиков событий. В данном случае необходимо создать обработчики для всех трех кнопок. В итоге в файле ControlElementsDlg.cpp у вас появится код:
…
void CControlElementsDlg::OnBtnCalc()
{
// TODO: Add your control notification handler code here
}
void CControlElementsDlg::OnBtnShow()
{
// TODO: Add your control notification handler code here
}
void CControlElementsDlg::OnBtnExit()
{
// TODO: Add your control notification handler code here
}
Программная реализация
Теперь мы готовы непосредственно перейти к программной реализации алгоритма решения поставленной задачи.
В самом начале файла ControlElementsDlg.cpp подключите библиотеки math.h и fstream.h:
#include <math.h>
#include <fstream.h >
Далее модифицируйте методы OnBtnCalc(), OnBtnShow() и OnBtnExit() так, как показано в Листинге 9:
| Листинг 9 |
void CControlElementsDlg::OnBtnCalc()
{
// TODO: Add your control notification handler code here
UpdateData(TRUE);
double dDeltaH = 0.25; // dDH - шаг по координате, м
double dCurH; // dH - текущая координата (глубина), м
double dCurR; //dR - текущий радиус газового пузырька, мм
double dRo = 1000.; //dRo - плотность воды, кг/м**3
double dG = 9.81; //dG - ускорение свободного падения, м/с**2
double dPatm = 1.01E5; // dPatm - нормальное атмосферное давление, Па;
double dA; // dA - вспомогательная величина
ofstream OutFile;
OutFile.open("bubble.txt"); //Открытие потока OutFile для записи
// файл необходим для визуализации решения
dCurH = m_H0;
//НАЧАЛО ГЛАВНОГО ЦИКЛА
while (dCurH >= 0)
{
dA = (dPatm + dRo * dG * m_H0) / (dPatm + dRo * dG * dCurH);
dCurR = m_R0 * pow(dA, 0.33);
OutFile << dCurH << "\t" << dCurR << "\n";
|
|
|
dCurH = dCurH - dDeltaH;
}
// КОНЕЦ ГЛАВНОГО ЦИКЛА
OutFile.close(); // Закрытие потока OutFile
// Вывод конечного радиуса
char szBuf[64];
sprintf(szBuf, "Конечный радиус %g", dCurR);
m_CurR = szBuf;
UpdateData(FALSE);
}
void CControlElementsDlg::OnBtnShow()
{
// TODO: Add your control notification handler code here
// Получаем указатель на местодержатель
CWnd* pWnd = (CWnd*)GetDlgItem(IDC_DRAW_AREA);
// Если указатель не пустой то приступаем к визуализации
if (pWnd)
{
// Создаем контекст устройства
CClientDC dc(pWnd);
CRect rect;
// Получаем клиентскуя область окна-местодеражателя
pWnd->GetClientRect(&rect);
// Заполняем фон белым цветом
dc.FillRect(&rect, NULL);
// Расчитываем масштабный коэфициент по оси х
double dScale = (rect.right - rect.left) / 41.;
char szBuf[256];
// Объявляем дискриптор файла
HANDLE hFile;
// Открывем файл с заданными параметрами
hFile = CreateFile("bubble.txt", // open bubble.txt
GENERIC_READ, // open for reading
0, // no share
NULL, // no security
OPEN_EXISTING, // existing file only
FILE_ATTRIBUTE_NORMAL, // normal file
NULL); // no attr. template
// Проверяем открылся ли файл
if (hFile == INVALID_HANDLE_VALUE)
{
return;
}
// Получаем размер файла
DWORD dwFileSize = GetFileSize(hFile, NULL);
// Создаем динамический массив
char* pBuf = new char[ dwFileSize + 1 ];
// Обнуляем элементы массива
memset(pBuf, 0, dwFileSize + 1);
DWORD dwBytesReaded;
// Читаем файл в память
ReadFile(hFile, pBuf, dwFileSize, &dwBytesReaded, NULL);
// Закрываем файл
CloseHandle(hFile);
// Определяем символы разделители слов
char seps[] = " \t\n\r";
char *token;
int i = 0;
// Получаем первое слово
token = strtok(pBuf, seps);
// Цикл «пока есть слова»
while (token!= NULL)
{
double x, y;
// Преобразуем слово в значение глубины
x = atof(token);
// Получаем следующее слово
token = strtok(NULL, seps);
if (token == NULL)
{
return;
}
// Преобразуем слово в значение радиуса
y = atof(token);
// Выводим значения глубины и радиуса
sprintf(szBuf, "Текущий радиус %g", y);
m_CurR = szBuf;
sprintf(szBuf, "Текущая глубина %g", x);
m_CurH = szBuf;
UpdateData(FALSE);
// Рисуем график
dc.MoveTo(ceil(i * dScale), rect.bottom - 1);
dc.LineTo(ceil(i * dScale), rect.bottom - 1 - y * (rect.bottom - rect.top)/ 10);
token = strtok(NULL, seps);
i++;
// Делаем задержку по времени
Sleep(300);
}
// Удаляем динамический массив
delete[] pBuf;
}
}
void CControlElementsDlg::OnBtnExit()
{
// TODO: Add your control notification handler code here
CDialog::OnOK();
}
Дадим краткие пояснения по содержанию Листинга 1.
Код функции OnBtnCalc() не должен вызывать у вас вопросов т.к. он основан на материале первого семестра. А вот функцию OnBtnShow() мы рассмотрим более подробно.
В строке:
CWnd* pWnd = (CWnd*)GetDlgItem(IDC_DRAW_AREA);
мы получаем указатель на окно-местодержатель в которое намереваемся выводить график. Функция GetDlgItem() позволяет получить указатель на любой элемент управления расположенный на форме диалога. В данном случае нас интересует элемент с идентификатором IDC_DRAW_AREA. Напомним, что это был элемент Picture. Если заданный элемент существует, и мы получили корректный указатель на него, то выполняет дальнейшее тело функции OnBtnCalc(). В противном случае все тело функции игнорируется и мы выходим из нее.
В строке:
CClientDC dc(pWnd);
создается так называемый контекст устройства. На данном этапе воспринимайте контекст устройства как холст на котором осуществляется рисование. Как в реальном мире вы можете рисовать на листике бумажки, на стене, на асфальте так и в Windows вы можете рисовать на различных контекстах соместимых с различными устройствами. Это могут быть контексты совместимые с каким-либо окном программы, контексты совместимые с экраном монитора, контексты совместимые с принтером, контексты в памяти и т.д. В нашем случае мы создаем контекст совместимый с окном ограниченным элементом Picture.
Далее мы определяем координаты области в которой собираемся рисовать:
CRect rect;
// Получаем клиентскуя область окна-местодеражателя
pWnd->GetClientRect(&rect);
И заполняем ее белым фоном:
dc.FillRect(&rect, NULL);
Структура CRect содержит в себе 4 координаты (right, left, top, bottom). Мы используем ее для получения правой, левой, верхней и нижней границ области рисования.
Исходя из условия задачи (глубина 10 м, шаг 0.25 м) мы можем грубо расчитать масштабный коэффициент по оси х:
double dScale = (rect.right - rect.left) / 41.;
Далее мы ставим перед собой задачу загрузить содержимое файла bubble.txt в память.
Для открытия файла мы пользуемся фанкцией CreateFile. Получив размер файла:
DWORD dwFileSize = GetFileSize(hFile, NULL);
мы определяем объем необходимой памяти для загрузки содержимого файла.
В строке:
char* pBuf = new char[ dwFileSize + 1 ];
собственно и происходит выделение памяти и создание так называемого динамического массива pBuf. Так как pBuf фактически является строкой символов прочитанных из файла, то создаем его на один символ больше чем размер файла. Последним элементом массива pBuf будет 0 (не путать с символом ‘0’). Как правило, 0 означает конец строки и таким образом мы обеспечиваем корректную работу стандартных функций обработки строковых данных, которые в противном случае могли бы выйти запределы отведенной памяти.
После чтения содержимого файла:
ReadFile(hFile, pBuf, dwFileSize, &dwBytesReaded, NULL);
мы его закрываем функцией CloseHandle().
Далее функцией strtok() мы выделяем из буферной строки pBuf очереные слова. Символы-раздели слов задаются в строке:
char seps[] = " \t\n\r";
В данном случае это пробел, табуляция и символы начала новой строки.
Цикл
while (token!= NULL)
выполняется до тех пор пока в pBuf. Признаком наличия слова есть неравенство NULL указателя token. Как только token становится равным NULL это означает, что все слова выделены и мы можем завершать цикл.
Внутри цикла идет преобразование слов в соответствующие числовие значения:
x = atof(token);
…
y = atof(token);
В качестве учебного элемента показано обратное преобразование чисел x и y в строку для вывода в элементы Static text.
sprintf(szBuf, "Текущий радиус %g", y);
m_CurR = szBuf;
sprintf(szBuf, "Текущая глубина %g", x);
m_CurH = szBuf;
Для рисования графика используются две функции класса CClientDC:
dc.MoveTo(ceil(i * dScale), rect.bottom - 1);
dc.LineTo(ceil(i * dScale), rect.bottom - 1 - y * (rect.bottom - rect.top)/ 10);
Первая перемещает курсор в заданные координаты. Вторая рисует линию из текущего положения курсора в заданные координаты.
Функция ceil() округляет аргумент до ближайшего целого снизу. Это необходимо делать потому, что аргументы функций MoveTo() и LineTo() должны быть целочисленными.
Обратите внимание на то, что для расчета аргумента у функции LineTo() используется целочисленная арифметика, и поэтому там нужды в округлении не возникает.
Теперь если вы запустите программу на выполнение и введете исходные данные соответствующие условию задачи (радиус – 5, глубина – 10) то после нажатия кнопок «Расчет» и «Визуализация» окно вашей программы будет напоминать вид приведенный на рис. 40.
Попробуйте вводить различные исходные данные и проанализируйте результат.
Рис. 40
Алгоритм работы программы
Попытаемся теперь составить общий алгоритм работы программы. Обратите внимание на то, что имеется ввиду не частный алгоритм расчета, а именно общий алгоритм работы всей программы в целом.
Прежде всего еще раз запустим программу и попытаемся сформулировать ее отличия (кроме визуального интерфейса) от консольных приложений которые вы создавали в первом семестре.
В нашей программе ControlElements нет жесткого порядка действий как это было реализовано в консольных приложениях. Вы можете вводить исходные данные в любом порядке. Если файл «bubble.txt» существует, то кнопку «Расчет» можно не нажимать, а сразу визуализировать решение нажав кнопку «Визуал».
Как видите, наша программа ControlElements обладает большей гибкостью по сравнению с консольными приложениями, которые вы делали ранее. Можно сказать, что она позволяет в любой момент времени делать любое действие. Представить такую концепцию в виде блок-схемы или словесного алгоритма весьма проблематично. Поэтому мы воспользуемся для формирования алгоритма работы программы своего рода диаграммой которую будем называть моделью поведения программы.
Для понимания того, что мы сибираемся изобразить на диаграмме, нам необходимо принять два постулата.
Давайте сначала вспомним потоки ввода/вывода которые вы использовали в консольных приложениях. Вы уже знаете, что эти потоки своего рода «органы чувств» программы при помощи которых она может общатся с внешними объектами (клавиатура, мышь, экран, принтер и т.д.) или с другими программами. Посредством входных потоков в программу поступают события от клавиатуры и мышки. Посредством выходных потоков программа посылает различную информацию во внешние устройства и другие программы.
Обобщим этот механизм и примем первый постулат. взаимодествие программы с другими объектами происходит посредством СООБЩЕНИЙ.
С каждым сообщением могут передаваться данные. Так, например, будем считать, что если на клавиатуре нажимается кнопка, то в программу приходит сообщение о том, что нажата такая-то кнопка.
На пользовательском интерфейсе нашей программы присутсвуют три кнопки «Расчет», «Визуал» и «Выход». Будем считать, что при нажатии на каждую кнопку в программу приходит соответствующее сообщение.
Механизм того, как приходят и отравляются сообщения нас пока не интересует. Важно, что он есть.
Теперь примем второй постулат. В каждый момент времени программа занимается выполнением какого-либо действия. Обратите внимание на то, что бездействие тоже является деятельностью.
Таким образом, можно сказать, что в различные моменты времени программа может находится в неких состояниях связанных с выполнением различных действий.
На рис. 41 приведена упрощенная модель поведения нашей программы.
Рис. 41.
Овалами отображены состояния. Каждое состояние имеет свое условное название. Возможные переходы между состояниями показаны стрелками. Рядом с каждой стрелкой отмечено событие котрое вызывает переход в новое состояние.
Обратите внимание на то, что диаграмма на рис. 41 является своего рода циклом. Входом в этот цикл является событие “Старт”. Это, например, может быть факт запуска программы. Если же возникло событие “Выход” (нажата соответствующая кнопка), то происходит выход из цикла. Сам же цикл заключается в том, что программа периодически переходит в состояния “Расчет” и “Визуализация” при нажатии соответствующих кнопок, причем порядок нажатия этих кнопок не имеет значения. Можно даже сказать, что данный цикл является “жизненным циклом” программы. Он демонстрирует модель повеждения программы от момента ее запуска, до момента ее завершения.
Следует отметить, что имена событий и состояний целесообразно делать различными иначе может возникнуть путаница. В нашем случае когда мы говорим “Расчет” мы не можем определить, что имеется ввиду состояние, событие или кнопка интерфейса.
Давайте теперь сравним нашу модель с имеющимся программным кодом.
Рис. 42.
Откройте в окне Workspace закладку ClassView и просмотрите перечень функций класса CControlElementsDlg (рис. 42). Все функции которые начинаются на On… являются обработчиками которые вызываются в момент прихода в программу соответствующего сообщения.
Обработчик OnBtnCalc() является аналогом действия выполняемого в состоянии «Расчет» нашей модели. Он вызывается при нажатии на кнопку «Расчет» на пользовательском интерфейсе.
Обработчик OnBtnShow() является аналогом действия выполняемого в состоянии «Визуализация», а обработчик OnBtnExit() позволяет завершить выполнение программы при нажатии на кнопку «Выход».
К сожалению, мы не можем явно увидить события генрируемые по завершению расчета или визуализации. Эту задачу берет на себя операциооная система и соответствующий программный код скрыт глубоко в системных библиотеках функций. Мы можем только утверждать, что по завершении определенного действия программа всегда возвращается в состояние ожидания прихода новых сообщений.
Теперь рассмотрим другие обработчики, которые были добавлены в программу автоматически при создании проекта.
Было бы наивно полагать, что в нашу программу приходит всего 3 сообщения. На самом деле их гораздо больше, но большая их часть просто игнорируется до тех пор пока вы не создадите соответствующий обработчик. Например, к таким относятся сообщения о движении мышки и нажатии ее клавиш, сообщения от клавиатуры и т.д.
Операционная система в которой запущена программа также может посылать ей определенные сообщения. Так функция OnPaint() является обработчиком системного сообщения WM_PAINT которое посылается в случае необходимости перерисовать окно программы. Поэтому функция OnPaint() всегда автоматически добавляется в проект на основе диалогового класса.
Остальные функции также являются обработчиками различных событий, но их рассмотрение вынесено в рамки лекционного материала.
|
|
|
