 |
Результаты расчета значений погрешностей
|
|
|
|
Практическая работа № 1
Определение погрешности средств измерений
Цель работы: изучение методов прикладной статистики в метрологии при оценке погрешностей окончательного результата измерения или при оценке погрешности метода измерений.
Теоретические сведения
Погрешность результата измерения - это разница между результатом измерения хизм и истинным значением хист измеряемой величины:
Δ х = хизм - хист
Она указывает границы неопределенности значения измеряемой величины.
Погрешность средства измерения - разность между показанием СИ и истинным (действительным) значением измеряемой ФВ. Она характеризует точность результатов измерений, проводимых данным средством.
В зависимости по характеру проявления погрешности делятся на случайные, систематические, прогрессирующие и грубые (промахи).
Случайная погрешность - составляющая погрешности измерения, изменяющаяся случайным образом (по знаку и значению) в серии повторных измерений одного того же размера ФВ, проведенных с одинаковой тщательностью в одних и тех же условиях. В появлении таких погрешностей не наблюдается какой-либо закономерности, они обнаруживаются при повторных измерениях одной и той же величины в виде некоторого разброса получаемых результатов.
Систематическая погрешность - составляющая погрешности измерения, остающаяся постоянной или закономерно меняющаяся при повторных измерениях одной и той же ФВ. Их отличие - могут быть обнаружены, предсказаны и почти полностью устранены введением соответствующей поправки.
Систематические погрешности рассматривается по составляющим в зависимости от источников ее возникновения, причем различают методическую, инструментальную и субъективную составляющие погрешности.
|
|
|
Субъективные систематические погрешности связаны с индивидуальными особенностями оператора. Как правило, эти погрешность возникает из-за ошибок в отсчете показаний и неопытности оператора. В основном же систематические погрешности возникают из-за методической и инструментальной составляющих.
Методическая составляющая погрешности обусловлена несовершенством метода измерения, приемами использования СИ, некорректностью расчетных формул и округления результатов, в результате чего измеряемая величина на выходе СИ преобразуется в другую величину.
Инструментальная составляющая возникает из-за собственной погрешности СИ, определяемой классом точности, влиянием СИ на результат и ограниченной разрешающей способности СИ.
Систематические погрешности являются следствием определенных недостатков методики и СИ, ошибок экспериментатора, неполного учета всех особенностей измеряемой величины и условий эксперимента.
Прогрессирующая погрешность - это непредсказуемая погрешность, медленно меняющаяся во времени. Они могут быть скорректированы поправками только в данный момент времени, а далее вновь непредсказуемо изменяются; их изменения во времени - это нестационарный случайный процесс.
Грубая погрешность (промах) - это случайная погрешность результата отдельного наблюдения, входящего в ряд измерений, которая для данных условий резко отличается от стальных результатов этого ряда. Они возникают из-за ошибок или неправильных действий оператора, кратковременных резких изменений условий проведения измерений.
Абсолютная погрешность - это погрешность, выраженная в тех же единицах, что и измеряемая величина. ΔХизм=Х-Хист=Х-Хср, Х-результат измерения. Если неизвестно Хист, используют Хср-среднее арифметическое нескольких измерений.
|
|
|
Относительная погрешность представляет собой отношение абсолютной погрешности к истинному значению измеряемой величины и выражается в процентах или долях измеряемой величины. σ=(Δ/Хист)*100.
Приведенная погрешность - это погрешность, выраженная отношением абсолютной погрешности СИ к условно принятому значению физической величины, которое постоянно во всем диапазоне или в некоторой его части γ=ΔХизм/Хn, где Xn-нормирующее значение.
- по условиям измерения (статические и динамические).
Статическая погрешность - погрешность результата измерений, свойственная условиям статического измерения, не зависящая от скорости измерения.
Динамическая погрешность - погрешность результата измерений, свойственная условиям динамического измерения, зависящая от скорости изменения измеряемой величины во времени.
- по зависимости абсолютной погрешности от значений измеряемой величины различают погрешности:
Аддитивные Δа, не зависящие от измеряемой величины;
Мультипликативные Δм, которые прямо пропорциональны измеряемой величине;
Нелинейные Δн, имеющие нелинейную зависимость от измеряемой величины.
- по влиянию внешних условий различают основную и дополнительную погрешности СИ.
Основной называется погрешность СИ, определяемая в нормальных условиях его применения.
Дополнительной называется погрешность СИ, возникающая вследствие отклонения какой-либо из влияющих величин.
Оценивание погрешностей производится с целью получения объективных данных о точности результата измерения. Точность результата измерения характеризуется погрешностью.
Характеристики погрешности принято делить на точечные и интервальные. К точечным относятся СКО случайной погрешности и предел сверху для модуля систематической погрешности, к интервальным - границы неопределенности результата измерения. Если эти границы определяются как отвечающие некоторой доверительной вероятности, то они называются доверительными интервалами. Если же минимально возможные в конкретном случае границы погрешности оценивают так, что погрешность, выходящую за них, встретить нельзя, то они называются предельными (безусловными) интервалами. Оценивание погрешностей может проводится до (априорное) и после (апостериорное) измерения.
|
|
|
Априорное оценивание - проверка возможности обеспечить требуемую точность измерений, проводимых в заданных условиях выбранным методом с помощью конкретных СИ.
Оно проводится в случаях:
- нормирования MX СИ;
- разработки методик выполнения измерений;
- выбора средств измерений для решения конкретной измерительной задачи;
- подготовки измерений, проводимых с помощью конкретного СИ. Апостериорную оценку проводят в тех случаях, когда априорная оценка
неудовлетворительна или получена на основе типовых MX, а требуется учесть индивидуальные свойства используемого СИ.
Задания для расчета
Задача 1. Для прибора с преобладающими аддитивными погрешностями рассчитать значения абсолютных, относительных и приведенных основных погрешностей измерений. Результаты представить в виде таблицы и графиков. Исходные данные задаются преподавателем.
Задача 2. Для прибора с преобладающими мультипликативными погрешностями рассчитать зависимость абсолютных и относительных основных погрешностей от результата измерений. Результаты представить в виде таблицы и графиков. Исходные данные задаются преподавателем.
Примеры решения задач
Задача 1. Амперметром класса точности 2,0 со шкалой 0...50 А измерены значения тока 0, 5, 10, 10, 25, 30, 40, 50 А. Рассчитать зависимости абсолютной, относительной и приведенной основных погрешностей от результата измерений. Результаты представить в виде таблицы и графиков.
Решение
Для записи результатов формируем таблицу (табл. 1), в столбцы которой будем записывать измененные значения I, абсолютные Δ I, относительные δI и приведенные γI погрешности.
В первый столбец записываем заданные в условии задачи измеренные значения тока: 0, 5, 10, 20, 25, 30,40, 50 А.
Класс точности амперметра задан числом без кружка, следовательно, приведенная погрешность, выраженная в процентах, во всех точках шкалы не должна превышать по модулю класса точности, т.е. | γI |< 2 %.
|
|
|
При решении задачи рассмотрим худший случай | γI | = 2 %, когда приведенная погрешность, принимает максимальное по абсолютной величине значение, что соответствует γI = +2 % и γI = - 2 %. Данные значения приведенной погрешности заносим в четвертый столбец табл. 1.
Таблица 1
Результаты расчета значений погрешностей
| I | Δ I | δI | γI |
| ±1 | ± 
| ±2 | |
| ±1 | ±20 | ±2 | |
| ±1 | ±10 | ±2 | |
| ±1 | ±5 | ±2 | |
| ±1 | ±4 | ±2 | |
| ±1 | ±3,33 | ±2 | |
| ±1 | ±2,5 | ±2 | |
| ±1 | ±2 | ±2 |
Из формулы 
выражаем абсолютную погрешность 
.
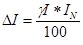За нормирующее значение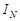 
принимаем размах шкалы, так как шкала амперметра содержит нулевую отметку, т.е. 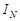= = |50А - 0А| == 50 А.
Абсолютная погрешность равна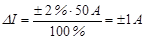 
во всех точках шкалы прибора. Заносим данное значение во второй столбец таблицы.
Значения относительной погрешности будем рассчитывать по формуле 
;
при I = 0 А 
;
при I = 5 А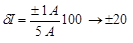 
%.
Значения относительной погрешности для остальных измеренных значений тока рассчитываются аналогично.
Полученные таким образом значения относительной погрешности заносим в третий столбец.
По данным таблицы 1 учитывая что погрешности могут быть как положительными, так и отрицательными, строим графики зависимостей абсолютной Δ I, относительной δI и приведенной γI погрешностей от результата измерений I (рис. 1).
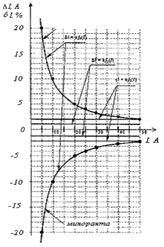
Рис. 1. Зависимости абсолютной,
относительной и приведенной погрешностей
от результата измерений для прибора с
преобладающими аддитивными погрешностями
 |
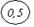Задача 2. Вольтметром класса точности со шкалой (0...100) В измерены значения напряжения 0, 10, 20, 40, 50, 60, 80.100 В. Рассчитать зависимости абсолютной и относительной погрешностей от результата измерений. Результаты представить в виде таблицы и графиков.
Решение
Для записи результатов формируем таблицу (табл. 2), в столбцы которой будем записывать измеренные значения V, абсолютные Δ V относительные δV погрешности.
В первый столбец записываем заданные в условии задачи измеренные значения тока: 0, 10, 20, 40, 50, 60, 80,100 В.
Класс точности вольтметра задан числом в кружке, следовательно, относительная погрешность, выраженная в процентах, во всех точках шкалы не должна превышать по модулю класса точности, т.е.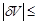 
0,5 %.
При решении задачи рассмотрим худший случай, т. е.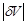 
= 0,5 %, что соответствует значениям δV = +0,5 % и δV = -0,5 %.
Примем во внимание опыт решения задачи 1, из которого видно, что результаты вычисления, выполненные для положительных и отрицательных значений погрешностей, численно совпадают друг с другом и отличаются только знаками «+» или «-». Поэтому дальнейшие вычисления будем производить только для положительных значений относительной погрешности δV = = 0,5 %, но при этом будем помнить, что все значения второго и третьего столбцов табл. 2 могут принимать и отрицательные значения.
|
|
|
Таблица 2
|
|
|
