 |
Теория метода и описание установки
|
|
|
|
Удельной теплоемкостью газа называется величина, численно равная количеству теплоты, которое необходимо сообщить единице массы газа, чтобы увеличить температуру на 1°.
Для газов эта величина зависит от условий, при которых производится нагревание. Различают нагревание при постоянном объеме (изохорический процесс) и при постоянном давлении (изобарический процесс). Соответственно имеют теплоемкость газа при постоянном объеме CV и удельную теплоемкость газа при постоянном давлении CP, причем CP всегда больше, чем CV . Это объясняется тем, что при нагревании газа при постоянном объеме, вся теплота, сообщаемая газу, идет на увеличение внутренней энергии и газ при этом никакой работы не производит:
.
При нагревании же газа при постоянном давлении, помимо теплоты, идущей на увеличение внутренней энергии, часть теплоты расходуется на совершение работы D A при расширении газа:
.
Эта формула имеет обоснование в первом законе термодинамики (общий закон сохранения энергии).
Непосредственно измерение CP и особенно CV экспериментально оказывается сложным, т.к. теплоемкость газа составляет ничтожную долю теплоемкости сосуда, в котором он помещается, и изменения, вследствие этого будут ничтожными. Проще измерить отношение удельных теплоемкостей (коэффициент Пуассона):
. (1)
Численное значение g зависит от числа степеней свободы молекул, из которых состоит газ. Поэтому для одно-, двух- и трехатомных газов коэффициент g различный.
Коэффициент Пуассона входит в уравнение для адиабатического процесса:
, (2)
где P - давление газа, V - объем газа.
Именно поэтому адиабатический процесс используется для измерения g газов в лабораторных условиях.
|
|
|
Адиабатическим процессом называют процесс, протекающий без теплообмена с окружающей средой. Этот процесс является идеальным, т.к. осуществить в действительности полную теплоизоляцию газа от внешней среды невозможно. Однако на практике мы часто встречаемся с процессами, весьма близкими к адиабатическим. Такими можно считать быстрое расширение или сжатие газа, при котором газ не успевает войти в теплообмен с окружающей средой (например: взрыв в двигателе внутреннего сгорания, сжатия и растяжения, происходящие при распространении звука и др.). Таким образом, при адиабатическом расширении газ совершает работу, поэтому внутренняя энергия его убывает и температура понижается.
Изменение температуры и давления при адиабатическом процессе используется в данной лабораторной работе для определения g воздуха. Экспериментальная установка Клемана-Дезорма (рис.1) для измерения g состоит из стеклянного баллона А на 20-30 л, соединенного с манометром М и с насосом Н. С помощью крана К баллон может быт соединен с атмосферой.
Если при помощи насоса накачать в баллон некоторое количество воздуха, то давление и температура воздуха внутри баллона повысятся. Через некоторое время в результате теплообмена с окружающей средой температура воздуха сравняется с температурой внешней среды T 1. Установившееся давление в баллоне будет выше атмосферного
,
где P 1- атмосферное давление, h - добавочное давление, измеряемое разностью уровней жидкости в левом и правом коленах, U -образного манометра.
Примем это состояние воздуха в баллоне первым состоянием 1с параметрами P 1, V 1, T 1 (рис.2).
Если открыть на короткое время кран, то воздух в баллоне будет адиабатически расширяться. В результате, давление в баллоне сравняется с атмосферным, температура воздуха понизится до T 2, а удельный объем увеличится до V 2. Следовательно, после адиабатического расширения параметрами воздуха во втором состоянии будут P 0, V 2, T 2. Далее, через некоторое время в результате теплообмена с окружающей средой воздух в баллоне нагреется до температуры внешней cреды T 1, при этом удельный объем не изменится и будет равен V 2, а давление возрастет и будет опять выше атмосферного
|
|
|
,
где h 2- новая разность уровней в манометре.
Это третье (последнее) состояние воздуха характеризуется следующими параметрами P 2, V 2, T 1. Заметим, что V 1 и V 2 являются удельными объемами (отнесенными 
к единице массы газа) и не имеют ничего общего с объемом баллона A. Таким образом, воздух, заключенный в баллон, во время опытов проходит последовательно три состояния. Переход из состояния 1 в 2 происходит адиабатно, следовательно, эти состояния связаны уравнением Пуассона:
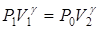. (2)
Переход из состояния 2в3 происходит без изменения объема (изохорно). В 1 и 3состояниях воздух имеет одну и ту же температуру, поэтому можно связать их с изотермическим уравнением Бойля-Мариотта:
. (3)
Чтобы решить уравнения (2) и (3) относительно g, возведем уравнение (3) в степень g и поделим почленно на (2), получим:
.
Откуда: 
; 
.
Логарифмируя последнее равенство, получим окончательно:
. (4)
В нашем случае давления P 0, P 1, P 2 мало отличаются друг от друга и разности логарифмов в (4) можно принять пропорциональными разности самих давлений:
. (5)
Таким образом, согласно (5), экспериментальное определение 
сводится к измерению h 1и h 2.
Задание и отчетность
1. Поверните в положение 2 кран К, соединяющий баллон с насосом, осторожно накачайте воздух в баллон до тех пор, пока разность уровней жидкости в манометре не достигнет 150-200 мм.
2. Закройте кран К поворотом на 90° и выждите 2-3 минуты, пока уровни жидкости в манометре не перестанут изменяться, произведите отсчет разности уровней в манометре h 1 с помощью миллиметровой линейки.
3. Поверните в положение 1 кранК и тот час же (как только уровни жидкости в манометре сравняются и прекратится шипение выходящего воздуха) его закройте поворотом на 90°.
4. Выждите 2-3 минуты, пока газ, охлажденный при расширении, снова нагреется до комнатной температуры. Произведите второй отсчет разностей уровней в манометре с помощью миллиметровой линейки.
|
|
|
5. Опыты по пунктам 1, 2, 3, 4 повторите 15 раз при разных значениях h 1.
6. Подставьте в формулу (5) значение h 1 и h 2, взятые из каждого отдельного опыта, вычислите соответственно g 1, g 2, g 3.
7. Вычислите среднее значение g ср и ошибки опыт D g ср, и окончательный результат запишите в виде g ср ± D g ср.
Результаты измерений занесите в таблицу:
| № № | h 1 | h 2 | g | g ср | D g | D g ср | g ср ± D g ср |
Контрольные вопросы
1. Какова связь g с числом степеней свободы молекул?
2. Можно ли пользоваться в лабораторной работе не нагнетающим, а разрежающим насосом?
3. Какое влияние на результат измерения окажет запаздывание при закрывании крана?
4. Считая воздух двухатомным газом, сравните полученный результат с табличным. Объясните расхождение результатов.
5. Какова связь между удельной и молярной теплоемкостью какого-либо вещества?
6. Чему равно отношение 
для смеси 3 молей аргона и 5 молей кислорода?
7. В каком случае нужна большая работа для увеличения давления идеального газа в n раз - при адиабатическом или при изотермическом сжатии?
8. Какой вклад в теплоемкость дают колебательные степени свободы?
9. Как объясняется зависимость теплоемкостей газов от температуры?
10. Выведете уравнение Пуассона.
11. Какие процессы называются политропными?
12. Получите уравнение политропы для идеальных газов.
Литература
1. И. К. Кикоин, А. К. Кикоин. Молекулярная физика. – М.: Наука, 1976.
2. Телесин Р. В. Молекулярная физика – М.: Высшая школа, 1973.
3. Сивухин Д. В. Курс общей физики. – М.: Наука, 1975 – т.2.
|
|
|
