Идентификация с помощью преобразования координат

Существует несколько стандартных видов функций, из которых легко можно получить линейную функцию путем преобразования координат. Эти функции указаны в таблице 2.

Таблица 2 Базисные функции с однократным и двойным преобразованиями координат

№	Вид ММ	Исходное уравнение	Преобразованные переменные		Преобразованное уравнение	Параметры ММ
			X	Y
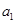
1	Линейная		x	y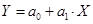
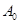
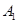
2	Степенная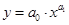
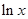
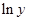
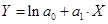
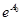
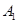
3	Показательная		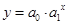x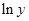
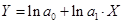
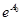
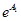
4	Показательно-гиперболическая
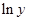
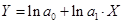
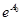
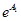
5	Гиперболическая		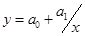	y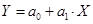
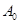
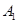
6	Обратная линейная		x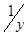
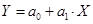
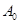
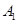
7	Обратная гиперболическая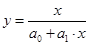
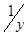
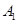
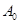
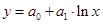
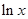
8	Логарифмическая			y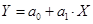
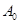
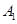
9	Обратная логарифмическая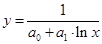
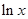
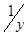
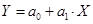
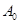
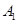
10	Гиперболическо-логарифмическая		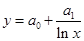	y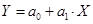
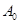
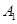
11	Обратная гиперболическо-логарифмическая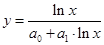
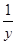
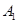
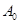
12	Показательно гиперболическо-логарифмическая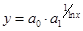
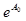
13	Обратная показательно гиперболическо-логарифмическая
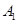
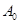
14	Обратная показательная		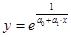x
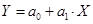
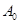
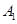
15	Обратная показательно-гиперболическая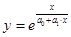
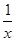
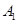
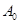
16	Обратная показательно-логарифмическая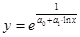

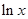
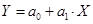
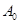
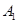
К процедуре выбора вида математической модели предъявляются противоречивые требования с одной стороны процедура выбора должна включать множество возможных вариантов ММ, с другой – должна быть выбрана одна иди ограниченное количество ММ, удовлетворяющих заданным условиям, выбор должен быть ограничен определенным набором функций, что позволяло бы проводить анализ этих ММ.

Удовлетворение этих требований в предлагаемой методике достигается за счет использования в качестве базовых ограниченного набора наиболее часто применяемых видов преобразова­ний прямо и обратно пропорционального и логарифмического, что сводит процесс выбора к сравнению ограниченного набора функций, обеспечивает эффективность сравнительного анализа этих моделей, и применением многоуровневого преобразования координат, позволяющего выбирать практически любой вид ММ при использовании ограниченного стандартного набора функций, введением во внешнем контуре выбора итерационных процедур и процедур оптимизации, обеспечивающих определение неизвестных параметров ММ, входящих как в левую, так и в правую части уравнений, а также нахождение необходимого количества ко эффициентов ММ.

Выбор вида математической модели – уравнения регрессии основан на физической сущности исследуемого процесса, опыте решения аналогичных задач, анализе исходной информации. В настоящее время отсутствуют общие формализованные методы выбора вида модели Однако доя наиболее часто встречающихся зависимостей с двумя параметрами такой предварительный выбор возможен на основе сравнительного анализа абсолютных по­грешностей каждого вида математических моделей для опреде­ленных значений х_i, вычисляемых с использованием массива экспериментальных данных х и у.

Если в основу систематизации и приведения ММ к линейно­му виду положить прямо пропорциональное X=х, логарифмиче­ское  и обратно пропорциональное  преобразования, то для двух переменных при однократном их преобразова­нии можно получить девять видов ММ (табл. 3.2), при двукрат­ном преобразовании – еще семь видов ММ (табл. 2)

Существенное расширение типов ММ достигается введением многоуровнего преобразования переменных х и у путём ис­пользования в качестве х и у. различных функций Например, если принять 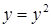, , то зависимость 1 (см. табл. 2) примет вид 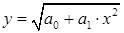, а шестая и седьмая функции перейдут, соответственно в уравнения

 или и

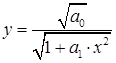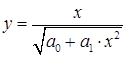 или .

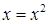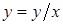При необходимости получения квадратичной зависимости достаточно принять , или , или 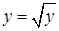 в уравнении 1.

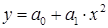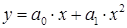В результате получим ММ , или , или

.

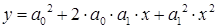Уравнение вида 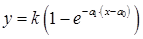, описывающее переходные процессы в технологических объектах управления, получается, если вместо у в математической модели 3 Принять величину  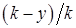, а уравнение 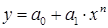, подстановкой в уравнение 1 переменной .

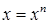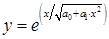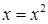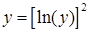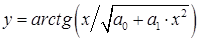Уравнение вида  может быть получено при , если для седьмой функции провести дополнительно двойное преобразование координаты  (сначала , затем ), а уравнение вида , если для той же функции провести двойное преобразование координаты  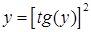(сначала , затем ).

Таким образом, проводя последовательно многоуровневое преобразование координат х и у в соответствии с одними и теми же известными функциями, можно получить практически любой вид ММ при использовании ограниченного набора стандартных функций.

Реализация данного метода представлена в приложении 3.

График полученной ММ проиллюстрирован на рисунке 7.

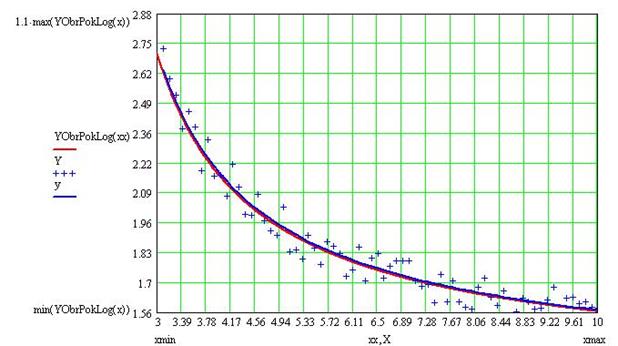
Рисунок 7 График полученной ММ

Как видно из приложения мы уменьшили среднеквадратическое отклонение от реальной кривой этим методом более, чем в три раза. Графики практически совпали.