Корпускулярно-волновой дуализм и постулаты общей теории относительности.

 

Корпускулярно-волновой дуализм означает, что частица одновременно обладает свойствами непрерывных электромагнитных волн и свойствами дискретных фотонов. Этот фундаментальный вывод был сделан физиками в XX века и вытекал из предшествующих представлений о свете.

 Ньютон считал, что свет - поток корпускул, т. е. поток прямолинейно летящих частиц вещества. Такая теория хорошо объясняла прямолинейное распространение света. Но возникали затруднения при объяснении законов отражения и преломления, а явления дифракции и интерференции совершенно не могли быть объяснены корпускулярной теорией. Поэтому возникла волновая теория света. Эта теория объясняла дифракцию и интерференцию, но возникали трудности с объяснением прямолинейного света.

 Только в XIX веке Ж. Френель, используя открытия других физиков, сумел объединить уже выведенные принципы в одну теорию, согласно которой свет - поперечная механическая волна. В дальнейшем Максвелл открыл, что свет - один из видов электромагнитного излучения. Но в начале XX века, благодаря открытиям Эйнштейна представления о свете опять изменились. Свет стал пониматься как поток фотонов. Но определенные свойства света прекрасно объяснялись и волновой теорией.

 Свет обладает как корпускулярными, так и волновыми свойствами. При этом существуют следующие закономерности: чем короче длина волны, тем ярче проявляются корпускулярные свойства, чем больше длина волны, тем ярче проявляются волновые свойства. Позднее французский физик Л. де Бройль высказал идею, что корпускулярно-волновой дуализм имеет универсальную природу, т.е. присущ всем частицам вещества. Позже эта гипотеза подтвердилась экспериментально.

 Корпускулярно-волновым дуализмом обладает и электрон. Многие концепции современной физики, такие как теория электромагнетизма, электродинамика, квантовая механика и др., основываются на представлении об электроне как носителе отрицательного электрического заряда. Однако представления о природе этого явления фактически отсутствуют.

Высказывалась гипотеза о том, что каждому протону в атоме соответствует свой собственный электрон и что природа отрицательного и положительного зарядов различается, в первую очередь, тем, что плотность распределения массы у протона возрастает от периферии к центру, а у электрона - от центра к периферии, т.е. электрон похож на мыльный пузырь, вся масса электрона может быть размазана по поверхности этого пузыря. Эта гипотеза в неявном виде присутствует в современных представлениях о сущности элементарных частиц, в соответствии с которыми элементарные частицы обладают пространственной протяженностью и своеобразной внутренней структурой.

 Образ пространственно-структурной и в то же время элементарной по своим свойствам частицы стал фактически общепринятым после экспериментального обнаружения американским физиком-экспериментатором Р.Хофштадтером пространственной «размазки» электрического заряда и магнитного момента протона.

 Считается, что свободная, невзаимодействующая микрочастица-это всего лишь математическая абстракция. Реальные физические частицы всегда взаимодействуют с вакуумными полями, испуская и поглощая виртуальные частицы[5].

 Вследствие этого вокруг каждой частицы образуется «облако» виртуальных частиц. И чем меньше масса испускаемых частиц, тем больше размеры образуемого ими облака. Продолжительность отдельных актов виртуальной диссоциации частицы (ее циклов «мигания») очень мала, но благодаря многократным их повторениям возникает постоянная, усредненная структура - «размазка» электрического заряда, магнитного момента, массы, которая становится все более плотной к центру частицы. В этом смысле говорят, что элементарная частица состоит из плотного центрального ядра - керна и рыхлой периферической оболочки.

 Такова «синтаксическая» суть современных представлений о природе элементарных частиц. И эти представления содержат в себе явный семантический смысл. В положительно заряженных частицах плотность электрического разряда, плотность массы, магнитного момента возрастает от периферии к центру. Тогда у отрицательно заряженных частиц этот вектор, в силу зеркальной симметрии, должен быть направлен в противоположную сторону, как бы характеризую противоположную волновую функцию частицы, которая по своей форме будет напоминать «мыльный пузырь», в котором процессы образования «облака» виртуальных частиц происходят вовнутрь. Таким образом, семантика этой гипотезы заключается в том, что противоположно заряженные частицы обладают и противоположными пространственно-временными формами, порождающими соответствующие противоположные заряды и магнитные моменты. Эти противоположно заряженные частицы характеризуются, в отличие от нейтральных частиц, энергетической активностью, 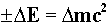где E - полная (собственная) энергия элементарной частицы. Следовательно, электрический заряд может характеризовать знак направления вектора энергетической активности частицы. Учитывая квантовый характер физических величин микромира, можно сказать, что энергетическая активность в элементарных частицах также должна быть квантованной и непосредственно связана с квантами электромагнитного поля.

Периодичность энергетической активности проявляется на всех уровнях иерархии материи и находит свое отражение в Едином Периодическом законе эволюции материи, в эволюции любого двойственного отношения. Эта периодичность вскрывает волновую природу двойственных отношений, характеризуя единство «частицы» и «волны» и порождая тем самым корпускулярно-волновой дуализм Единого Периодического закона, как в физике материи, так и в физике духа.

 Естественно, что такие структуры могут и должны обладать корпускулярно-волновым дуализмом. Но, к сожалению, корпускулярно-волновой дуализм трактуется только в вероятностном смысле. Так, из противоречия между гипотезой о вращении электрона вокруг протона по стационарным орбитам и экспериментом, согласно которым можно говорить только о вероятностных орбитах электрона, вытекает вывод об электронном облаке, которое образуют вероятностные орбиты. И физики уже давно смирились с этими фактами, не пытаясь проникнуть в их физическую природу.

 Общая теория относительности (ОТО) — современная теория тяготения, связывающая его с кривизной четырехмерного пространства-времени[6].

В своем, так сказать, классическом варианте теория тяготения была создана Ньютоном еще в XVII веке и до сих нор верно служит человечеству. Она вполне достаточна для многих, если не для большинства, задач современной астрономии, астрофизики, космонавтики. Между тем ее принципиальный внутренний недостаток был ясен еще самому Ньютону. Это теория с дальнодействием: в ней гравитационное действие одного тела на другое передается мгновенно, без запаздывания. Ньютоновская гравитация так же соотносится с общей теорией относительности, как закон Кулона с максвелловской электродинамикой. Максвеллу удалось изгнать дальнодействие из электродинамики. В гравитации это сделал Эйнштейн.

Начать рассказ следует с замечательной работы Эйнштейна 1905 года, в которой была сформулирована специальная теория относительности и которая завершила в идейном отношении развитие классической электродинамики. У этой работы несомненно были предшественники, среди которых нельзя не упомянуть работы Лоренца и Пуанкаре. В их статьях уже содержались многие элементы специальной теории относительности. Однако ясное понимание, цельная картина физики больших скоростей появились лишь в упомянутой работе Эйнштейна. Не случайно, несмотря на наличие прекрасных современных учебников, ее до сих нор можно рекомендовать для первого знакомства с предметом не только студентам, но и старшеклассникам.

Что же касается ОТО, то все ее основополагающие элементы были созданы Эйнштейном.

Впрочем, предчувствие того, что физика может быть связана с кривизной пространства, можно найти в трудах замечательных ученых прошлого века Гаусса, Римана, Гельмгольца, Клиффорда. Гаусс, который пришел к идеям неевклидовой геометрии несколько ранее Лобачевского и Бойаи, но так и не опубликовал своих исследований в этой области, не только считал, что «геометрию приходится ставить в один ряд не с арифметикой, существующей чисто a priori, а скорее с механикой». Он пытался проверить экспериментально, путем точных (для того времени) измерений геометрию нашего пространства. Его идея вдохновила Римана, полагавшего, что наше пространство действительно искривлено (а на малых расстояниях даже дискретно). Жесткие ограничения на кривизну пространства были получены из астрономических данных Гельмгольцем. Клиффорд считал материю рябью на искривленном пространстве.

Однако все эти блестящие догадки и прозрения были явно преждевременны. Создание современной теории тяготения было немыслимым без специальной теории относительности, без глубокого понимания структуры классической электродинамики, без осознания единства пространства-времени. Как уже отмечалось, ОТО была создана в основном усилиями одного человека. Путь Эйнштейна к построению этой теории был долгим и мучительным. Если его работа 1905 года «К электродинамике движущихся сред» появилась как бы сразу в законченном виде, оставляя вне поля зрения читателя длительные размышления, тяжелый труд автора, то с ОТО дело обстояло совершенно иначе. Эйнштейн начал работать над ней с 1907 года. Его путь к ОТО продолжался несколько лет. Это был путь проб и ошибок, который хотя бы отчасти можно проследить по публикациям Эйнштейна в эти годы. Окончательно задача была решена им в двух работах, доложенных на заседаниях Прусской Академии наук в Берлине 18 и 25 ноября 1915 года. В них были сформулированы уравнения гравитационного поля в пустоте и при наличии источников.

В последнем этапе создания ОТО принял участие Гильберт. Вообще значение математики (и математиков) для ОТО очень велико. Ее аппарат, тензорный анализ, или абсолютное дифференциальное исчисление, был развит Риччи и Леви-Чивита. Друг Эйнштейна, математик Гроссман познакомил его с этой техникой.

И все же ОТО — это физическая теория, в основе которой лежит ясный физический принцип, твердо установленный экспериментальный факт[7].

Факт этот но существу был установлен еще Галилеем. Он хорошо известен каждому успевающему старшекласснику: все тела движутся в поле тяжести (в отсутствие сопротивления среды) с одним и тем же ускорением, траектории всех тел с заданной скоростью искривлены в гравитационном поле одинаково. Благодаря этому, в свободно падающем лифте никакой эксперимент не может обнаружить гравитационное поле. Иными словами, в системе отсчёта, свободно движущейся в гравитационном поле, в малой области пространства-времени гравитации нет. Последнее утверждение — это одна из формулировок принципа эквивалентности.

Данное свойство поля тяготения отнюдь не тривиально. Достаточно вспомнить, что в случае электромагнитного поля ситуация совершенно иная. Существуют, например, подзаряженные, нейтральные тела, которые электромагнитного поля вообще не чувствуют. Так вот, гравитационно- нейтральных тел нет, не существует ни линеек, ни часов, которые не чувствовали бы гравитационного поля. Эталоны привычного евклидова пространства меняются в поле тяготения.

Геометрия нашего пространства оказывается неевклидовой.

Некоторое представление о свойствах такого пространства можно получить на простейшем примере сферы, поверхности обычного глобуса. Рассмотрим на ней сферический треугольник — фигуру, ограниченную дугами большого радиуса. (Дуга большого радиуса, соединяющая две точки на сфере, — это кратчайшее расстояние между ними: она естественный аналог прямой на плоскости.) Выберем в качестве этих дуг участки меридианов, отличающихся на 90^o долготы, и экватора (рис. 1). Сумма углов этого сферического треугольника отнюдь не равна сумме углов π,треугольника на плоскости:

Заметим, что превышение суммы углов данного треугольника над может быть выражено через его площадь S и радиус сферы R:

Можно доказать, что это соотношение справедливо для любого сферического треугольника. Заметим также, что обычный случай треугольника на плоскости тоже вытекает из этого равенства: плоскость может рассматриваться как сфера с R→∞

Перепишем формулу (2) иначе:

Отсюда видно, что радиус сферы можно определить, оставаясь на ней, не обращаясь к трехмерному пространству, в которое она погружена. Для этого достаточно измерить площадь сферического треугольника и сумму его углов. Иными словами, K (или R) является внутренней характеристикой сферы. Величину K принято называть гауссовой кривизной, она естественным образом обобщается на произвольную гладкую поверхность:

Здесь углы и площадь относятся к малому треугольнику на поверхности, ограниченному линиями кратчайших расстояний на ней, а кривизна, вообще говоря, меняется от точки к точке, является величиной локальной. И в общем случае, так же как и для сферы, K служит внутренней характеристикой поверхности, не зависящей от ее погружения в трехмерное пространство. Гауссова кривизна не меняется при изгибании поверхности без ее разрыва и растяжения. Так, например, конус или цилиндр можно разогнуть в плоскость, и поэтому для них, так же как для плоскости, K = 0.

На соотношения (3), (4) полезно взглянуть несколько иначе. Вернемся к рисунку 1. Возьмем на полюсе вектор, направленный вдоль одного из меридианов, и перенесем его вдоль этого меридиана, не меняя угла между ними (в данном случае нулевого), на экватор. Далее, перенесем его вдоль экватора, снова не меняя угла между ними (на сей раз π/2), на второй меридиан. И наконец, таким же образом вернемся вдоль второго меридиана на полюс. Легко видеть, что, в отличие от такого же переноса по замкнутому контуру на плоскости, вектор окажется в конечном счете повернутым относительно своего исходного направления на π/2, или на

Этот результат, поворот вектора при его переносе вдоль замкнутого контура на угол, пропорциональный охваченной площади, естественным образом обобщается не только на произвольную двумерную поверхность, но и на многомерные неевклидовы пространства. Однако в общем случае n-мерного пространства кривизна не сводится к одной скалярной величине K(x). Это более сложный геометрический объект, имеющий n²(n² - 1)/12 компонентов. Его называют тензором кривизны, или тензором Римана, а сами эти пространства — римановыми. В четырехмерном римановом пространстве-времени общей теории относительности тензор кривизны имеет 20 компонентов.

Однако роль ОТО отнюдь не сводится к исследованию малых поправок к обычной ньютоновской гравитации. Существуют объекты, в которых эффекты ОТО играют ключевую роль, важны стопроцентно. Это так называемые черные дыры.

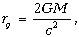Еще в XVIII веке Митчел и Лаплас независимо заметили, что могут существовать звезды, обладающие совершенно необычным свойством: свет не может покинуть их поверхность. Рассуждение выглядело примерно так. Тело, обладающее радиальной скоростью v, может покинуть поверхность звезды радиусом R и массой M при условии, что кинетическая энергия этого тела mv²/2 превышает энергию притяжения GMm/R,т.е. при v² > 2GM/R. Применение последнего неравенства к свету (как мы теперь понимаем, совершенно не обоснованное) приводит к выводу: если радиус звезды меньше чем

то свет не может покинуть ее поверхность, такая звезда не светит! Последовательное применение ОТО приводит к такому же выводу, причем, поразительно, правильный критерий количественно совпадает с наивным, необоснованным. Величина r_g, гравитационный радиус, уже встречалась раньше (см. формулу (7)).

Черная дыра — вполне естественное название для такого объекта. Свойства его весьма необычны. Черная дыра возникает, когда звезда сжимается настолько сильно, что усиливающееся гравитационное поле не выпускает во внешнее пространство ничего, даже свет. Поэтому из черной дыры не выходит никакая информация. Многочисленные результаты астрономических наблюдений дают серьезные основания полагать, что черные дыры — это не просто игра ума физиков-теоретиков, а реальные объекты, существующие по крайней мере в ядрах галактик[8].

 

 

⇐ Предыдущая123Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: