Образец таблицы для ввода исходных данных ОЗЛП

Таблица 1.1.

 

	A	B	C	D	E	F	G	H	I	J	K
		ПЕРЕМЕННЫЕ
	ФИЛИАЛЫ	АО1	АО2	АО3	АО4	АО5	АО6	АО7
	СЫРЬЕ			6.5		10.5
	Ограничение по сырью								Прибыль (целевая функция)
	КОЭФФ.								987.5
		ОГРАНИЧЕНИЯ
	ВИД продукции	Выход (из 1тн сырья) готового продукта	Расчетный объем продукции	ЗНАК	Макс. объем продукции
	ПРОД.1	0.2	0.1	0.15	0.2	0.25	0.1	0.3	3.6	<=	3.6
	ПРОД.2	0.2	0.2	0.15	0.1	0.1	0.2	0.1	2.025	<=	4.2
	ПРОД.4	0.1	0.15	0.2	0.1	0.15	0.2	0.1	2.875	<=	3.4
	ПРОД.5	0.1	0.1	0.1	0.1	0.1	0.1	0.1	1.7	<=	1.7

 

 

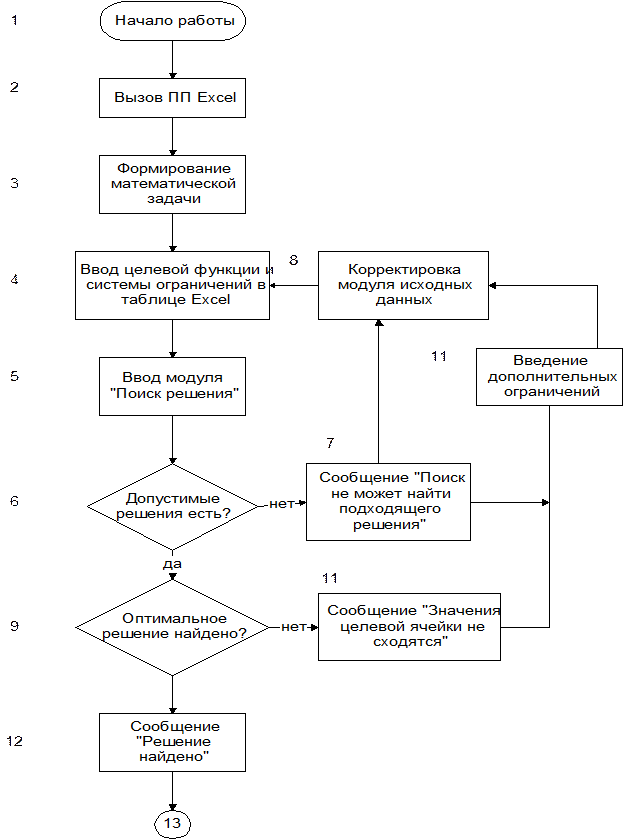
Рисунок 1.1. Алгоритм Автоматизированного решения ОЗЛП

Рисунок 1.1. (Продолжение)

 

Исполнение блока 4 (рисунок 1.1) происходит в следующей последовательности:

• Создание таблицы для ввода условий задачи (таблица 1.1),
• Ввод исходных данных,
• Ввод математической формулы для определения целевой функции,
• Ввод математических формул для определения объема выпуска каждого вида

продукции (левых частей ограничений задачи).

После создания формы таблицы 1.1 ввод исходных данных должен происходить в

следующие ячейки:

• В6:Н6 - коэффициенты при переменных в целевой функции (нормы прибыли),
• В9.Н12 - коэффициенты при переменных в ограничениях задачи (норма

расхода сырья);

• К9:К12 - правые части ограничений задачи (максимальные объемы выпуска

продукции),

• Y9:Y12- знаки ограничения задачи.

Остальные клетки таблицы 1.1 должны быть пустыми (за исключением клеток,

содержащих поясняющий текст). Далее в таблицу 1.1 следует ввести зависимость

для целевой функции, используя для этого подпрограмму "Мастер функций"

• Сделать активной ячейку 16, предназначенную для значения целевой функции,
• Вызвать "Мастер функции ",
• Перейти к категории "Математические",
• Вызвать функцию СУММПРОИЗВ, которая находит сумму произведений
• соответствующих элементов массивов;
• В окне Массива 1 ввести адрес ячеек В$3:Н$3, предназначенных для значений
• переменных Х1-Х7;
• В окне Массива 2 ввести адреса ячеек В6:Н6, предназначенных для
• коэффициентов целевой функции,
• Нажать кнопку "Готово*' (в ячейку 16 будет введена формула для вычисления значения целевой функции); при вводе исходных данных с помощью таблицы 1.1 F=O, т.к. равны 0 исходные значения переменных Х1/Х7.

Далее в ячейки I9:I12 следует ввести аналогичные формулы для вычисления левых частей ограничений задачи, которые также определяются как сумма произведений значений переменных Х1/Х7 на нормы выпуска соответствующего вида продукции.

Чтобы избежать многократного обращения к функции СУММПРОИЗВ, рекомендуется;

• Скопировать содержимое ячейки 16 в буфер,
• Сделать активной ячейку 19;
• "Вставить из буфера" формулу для определения суммы произведений,
• Скопировать ячейку 19 в ячейки I10:I12, обеспечив, таким образом, возможность вычисления суммы произведений для всех ограничений задачи.

При вводе исходных данных в ячейках I9:I12 будут нули, т.к. переменные Х1/Х7 имеют нулевые значения.

На этом заканчивается ввод исходных данных и подготовка необходимых расчетных формул.

Следующим этапом автоматизированного решения ОЗЛП является вызов модуля "Поиск решения" через опцию "Сервис"

В появившемся диалоговом окне модуля "Поиск решения" (рисунок 1.2) следует установить следующие параметры:

• Указать адрес целевой ячейки;
• Задать направление целевой функции: "Максимальному значению",
• В поле "Изменяя ячейки" ввести адреса искомых переменных $В$3;$Н$3,
• Выбор опции "Добавить" вызывает появление диалогового окна "Добавление ограничений" (рисунок 1.3), в котором последовательно задаются нижние или верхние границы для переменных задачи и ограничения по выпуску продукции.

Для указания нижних границ для переменных задачи следует:

• В окне "Ссылки на ячейки" указать адрес XI - $В$3,
• В окне "Ограничения " выбрать знаки для ввода в ограничение «>»;
• В правом окне указать адрес нижней границы для XI - $В$4;
• «Добавить»

 

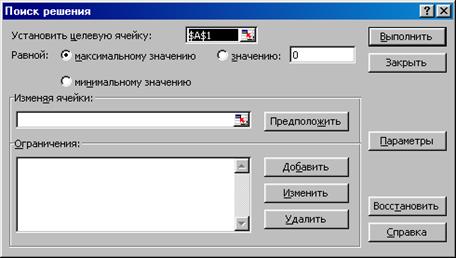
Рисунок 1.2. Диалоговое окно модуля "Поиск решения"

 

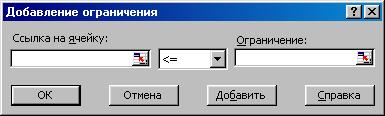
Рисунок 1.3. Окно «Добавление ограничения»

 

Аналогичным образом следует указать нижние границы для оставшихся Х2+Х7.

Далее в этом же диалоговом окне «Добавление ограничения» вводятся ограничения по выпуску продукции:

• В окне «Ссылки на ячейки» - адрес $I$9;
• В окне «Ограничения» выбор знака для ввода в ограничении «£»;
• В правом окне указать адрес правой части ограничений по первому виду продукции $K$9;
• «Добавить»;
• Аналогичным образом задаются ограничения по остальным видам продукции I10£K10,I11£K11,I12£K12;
• После ввода последнего ограничения вместо «Добавить» нажать ОК.

 

На экране появится диалоговое окно «Поиск решения» (рисунок 1.2) с введенными условиями.

Если в процессе решения задачи возникает необходимость изменения или удаления ограничений, это выполняется с помощью команды «Изменить» или «Удалить».

На этом заканчивается этап ввода условий задачи и происходит переход к этапу установки параметров решения, путем выбора команды «Параметры», после чего на экране появляется диалоговое окно «Параметры поиска решений» (рисунок 1.4).

С помощью команд, находящихся в данном диалоговом окне, задаются условия для решения задачи оптимизации всех классов. Следует учесть, что команды, используемые по умолчанию, подходят для решения большей части задач.

Параметр «Максимальное время» служит для назначения времени решения задачи в секундах. Максимально возможное время – 32767. Значение 100, используемое по умолчанию, подходит для решения большинства задач.

Параметр «Предельное число итераций» служит для назначения числа итераций, по умолчанию принимается равным 100.

Для решения ОЗЛП по симплекс-методу следует установить флажок «Линейная модель».

Остальные параметры поиска решения выбираются по умолчанию.

 

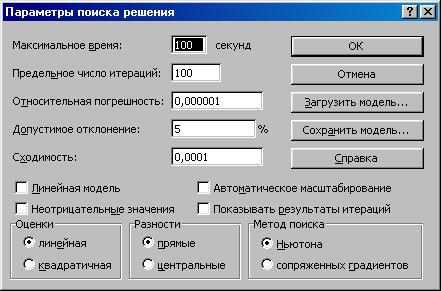
Рисунок 1.4. Диалоговое окно «Параметры поиска решения»

 

Далее выполняется команда ОК и на экране появляется основное окно модуля «Поиск решения» (рисунок 1.2).

Выбор в этом окне команды «Выполнить» инициирует автоматизированное решение ОЗЛП симплекс-методом, после чего на экране появится диалоговое окно «Результаты поиска решения» (рисунок 1.5)

Если решение найдено, то основные результаты решения будут показаны в поле таблицы 1.1.

В строке В3:Н3 окажутся значения искомых семи переменных, в клетке I6 – значение максимальной прибыли; в клетках I9:I12 – количество произведенной продукции различных типов (по вариантам задания).

 

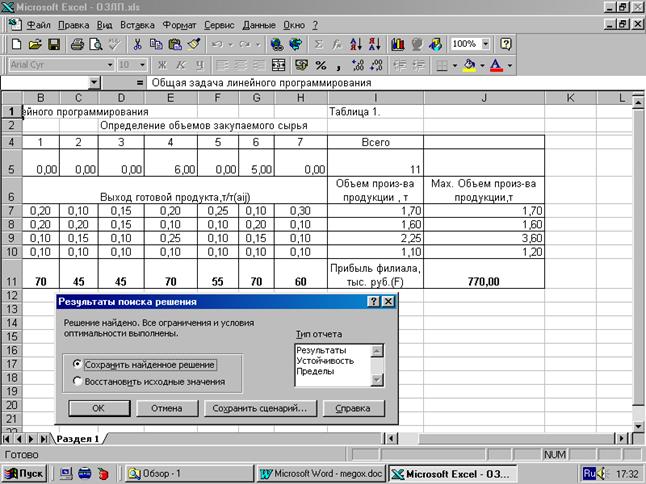
Рисунок 1.5 «Результаты поиска решения»

Таким образом, для варианта, представленного в таблице 1.1.

АО1=0 АО2=0 АО3=6,5

АО4=0 АО5=10,5 АО6=0 АО7=0

Следовательно, филиалу предприятия выгодно закупать сырьё только у акционерных обществ АОЗ и АО5 в количестве 6,5 и 10,5 тонн. При этом максимум прибыли предприятия составит 987,5 тыс. рублей и будут произведены следующие объемы продукции: предприятие 1 – 3,6 т, предприятие 2 – 2,025 т, предприятие 3 – 2,875 т, предприятие – 1,7т

Модуль «Поиск решения» не всегда находит оптимальные решения, в этом случае в окне «Результаты поиска решения» (рисунок 1.5) появляется сообщение «Значения целевой ячейки не сходятся».

При появлении подобного сообщения рекомендуется предпринять действия, предусмотренные блоками 8 и 11 алгоритма, показанного на рисунке 1.1.

Графическое представление результатов оптимального решения достигается с помощью построения различных видов диаграмм в соответствии с возможностями программы Excel по данным результатов таблицы 1.1

 

Экономический анализ полученного оптимального решения производится с помощью отчетов по результатам, устойчивости и пределам, вызываемым через диалоговое окно «Результаты поиска решения».

Отчет по результатам состоит из трех таблиц, показанных на рисунке 1.6.

В таблице «Целевая ячейка (максимум)» приведены адрес, исходное и результативное значение целевой функции.

В таблице «Изменяемые ячейки» находятся адреса, идентификаторы и значения всех искомых переменных задачи, определенных в таблице 1.1.

 

Целевая ячейка (Максимум)

Ячейка	Имя	Исходно	Результат
$I$6	Коэф.		987,5

 

Изменяемые ячейки

Ячейка	Имя	Исходно	Результат
$B$3
$C$3
$D$3		6.5	6.5
$E$3
$F$3		10.5	10.5
$G$3
$H$3

 

Ограничения

Ячейка	Имя	Значение	Формула	Статус	Разница
$I$9	Прод.1Лев.ч.	3,6	$I$9<=$K$9	Связанное
$I$10	Прод.2Лев. ч.	2,025	$I$10<=$K$10	Не связан.	2,175
$I$11	Прод.4Лев. ч.	2,875	$I$11<=$k$11	Не связан.	0,525
$I$12	Прод.5Лев. ч.	1,7	$I$12<=$K$12	Связанное
$B$3			$B$3>=$B$4	Связанное
$C$3			$C$3>=$C$4	Связанное
$D$3		6,5	$D$3>=$D$4	Не связан.	6,5
$E$3			$E$3>=$E$4	Связанное
$F$3		10,5	$F$3>=$F$4	Не связан.	10,5
$G$3			$G$3>=$G$4	Связанное
$H$3			$H$3>=$G$4	Связанное

 

Рисунок 1.6. Форма “Отчеты по результатам” модуля “Поиск решения”

 

В таблице " Ограничения " показаны результаты оптимального решения для граничных условий и ограничений задачи.

В графе "Формула" указаны зависимости, которые были введены в диалоговом окне "Поиск решения ", в графе «Значения» приведены величины объемов отдельных видов продукции и значения искомых «переменных задачи». В графе «Разница» показано количество не произведенной продукции. Если объем производства продукции данного типа равен максимально возможному, то в графе "Состояние" указывается связанное, при неполном производстве продукции в графе "Состояние" указывается "Не связанное", а в графе "Разница" - остаток. Для граничных условий приводятся аналогичные величины.

Отчет по устойчивости содержит информацию о том, насколько целевая ячейка чувствительна к изменениям ограничений и переменных (рисунок 1.7). Этот отчет имеет два раздела: один для изменяемых ячеек, а второй - для ограничений.

 

 

Изменяемые ячейки

Ячейка	Имя	Результ. значение	Редуцир. стоимость	Целевой коэффициент	Допустимое увеличение	Допустимое уменьшение 1
$B$3	АОI		-27,5		27,5	1E+30
$С$3	АО2		-12,5		12,5	1E+30
$D$3	АОЗ	6.5				1,666666667
$Е$3	АО4		-17,5		17,5	1E+30
$F$3	АО5	10,5			5,000000001
$G$3	АО6		-2,5		2,5	1E+30
$Н$3	АО7		-32,5		32,5	1E+30

 

Ограничения

Ячейка	Имя	Результ. значение	Теневая цена	Ограничение, правая часть	Допустимое Увеличение	Допустимое уменьшение
$l$9	Прод1 Лев.ч.	3.6		3,6	0,65	1,05
$I$10	Прод.2 Лев.ч.	2,025		4,2	1E+30	2,175
$I$11	Прод.4 Лeв.ч.	2,875		3,4	1E+30	0,525
$I$12	Прод.5 Лев.ч.	1,7		1,7	О,190909091	0,26

 

Рисунок 1.7. Форма «Отчета по устойчивости модуля «Поиск решения»

 

В разделе для изменяемых ячеек графа «Редуцированная стоимость» содержит значения дополнительных двойственных переменных, показывающих, как изменится целевая функция при принудительной закупке единицы сырья у данного акционерного общества.

Графа " Целевой коэффициент " показывает степень зависимости между изменяемой и целевой ячейками, те коэффициенты целевой функции

Графы "Допустимое увеличение " и "Допустимое уменьшение " показывают предельные значения приращения коэффициентов в целевой функции DСi,, при которых сохраняется оптимальное решение.

Для ограничений в графе "Теневая цена" приведены двойственные оценки Z,, которые показывают, как изменится целевая функция при изменении объема выпуска продукции на единицу.

В графах "Допустимое увеличение" и "Допустимое уменьшение" показаны размеры приращений объемов выпуска продукции Dbi, при которых сохраняется оптимальный набор переменных, входящих в оптимальное решение.

Отчет по пределам (рисунок 1.8) показывает, в каких пределах может измениться объем закупаемого сырья, вошедшего в оптимальное решение, при сохранении структуры оптимального решения.

В отчете указаны значения Xj в оптимальном решении и нижние пределы изменений значений Xj. Кроме этого, в отчете указаны значения целевой функции пи закупке данного типа сырья на нижнем пределе, а также верхние пределы изменений Xj и значения целевой функции при закупке сырья, вошедшего в оптимальное решение, на верхних пределах.

Первый раздел курсовой работы следует закончить рекомендациями предприятию по расширению программы выпуска ассортимента продукции, сделанными на основе экономического анализа приведённых выше отчётов.

 

Целевое
Ячейка	Имя	Значение
$I$6	Коэф.	987,5

 

Изменяемое
Ячейка	Имя	Значение
$B$3	АО1
$C$3	АО2
$D$3	АО3	6,5
$E$3	АО4
$F$3	АО5	10,5
$G$3	АО6
$H$3	АО7

 

Нижний предел	Целевое результат
	987,5
	987,5
	987,5
	357,0
	987,5
	987,5

 

Верхний предел	Целевое результат
	987,5
	987,5
6,5	987,5
	987,5
10,5	987,5
	987,5
	987,5

 

Рисунок 1.8. Форма отчета по пределам модуля «Поиск решений»

 

2. Автоматизированное решение транспортной задачи линейного программирования

⇐ Предыдущая1234Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: