|
m; 0) – вершина параболы (сдвиг вдоль оси x)
|
|
|
|
Формулы сокращенного умножения
| (a ± b)2= a 2±2 ab + b 2 | (квадрат суммы / разности) |
| (a ± b)3= a 3±3 a 2 b +3 ab 2± b 3 | (куб суммы / разности) |
| a 2- b 2=(a - b)(a + b) | (разность квадратов) |
a 3± b 3=(a ± b)(a 2 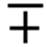 ab + b 2) ab + b 2)
| (сумма / разность кубов) |
Разложение квадратного трехчлена на множители
ax 2 +bx+c=a(x-x1)(x-x2)
Квадратное уравнение
ax2+bx+c=0; a¹0
D=b2– 4 ac – дискриминант квадратного уравнения
| D<0 | - нет корней | Теорема Виета | ||||
 a<0 a<0
|   a>0 a>0
| Если уравнение ax2+bx+c=0 имеет корни x1 и x2, то x1 + x2 = –b/a x1 × x2 = c/a | ||||
| D=0 |   - один корень - один корень 
| |||||
| 
| |||||
| Корни квадратного уравнения разных знаков, если c/a < 0 | ||||||
| D>0 | - два корня 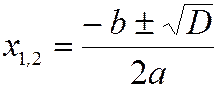
| |||||
 
|  
| x1>0; x2>0, если D³0 - b/a>0 c/a>0 | x1<0; x2<0, если D³0 - b/a<0 c/a>0 |
Исследование функций
| 1. Область определения, область значений функции 2. а) Четность – нечетность функции б) Периодичность функции 3. Точки пересечения графика с осями координат 4. Промежутки знакопостоянства 5. Промежутки монотонности 6. Экстремумы функции 7*. Поведение функции в точках разрыва и на концах области определения | y=x2-9
1. D(y)= R E(y)=[-9;+¥]
2. а) y(-x)= y(x) – функция четная, график симметричен отн-но Оy
б) функция непериодическая
3. С осью Ox: y =0 x1 =3, x2 = –3
С осью Oy: x = 0 y=–9
 4. + - + y
-3 3
y >0 при x Î(-¥;-3)È(3;+¥)
y <0 при x Î[-3;3]
5. y’=2x
Крит.точки: 2 x =0; x =0 4. + - + y
-3 3
y >0 при x Î(-¥;-3)È(3;+¥)
y <0 при x Î[-3;3]
5. y’=2x
Крит.точки: 2 x =0; x =0
  - + y’
æ 0 ä y
функция возрастает при x Î[0; +¥)
функция убывает при x Î(-¥;0)
6. xmin=0 y(0)=-9 - + y’
æ 0 ä y
функция возрастает при x Î[0; +¥)
функция убывает при x Î(-¥;0)
6. xmin=0 y(0)=-9
|
Приемы преобразования графиков
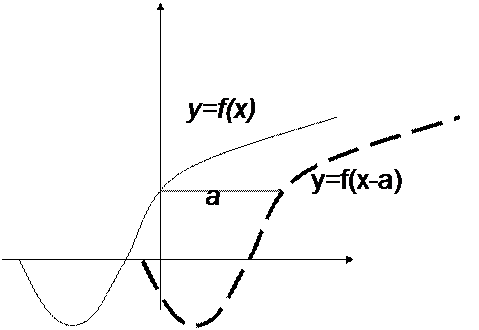
| 
| 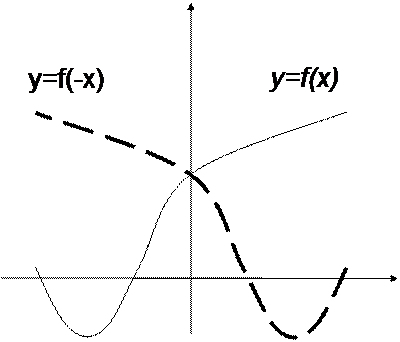
| ||||||

| 
| 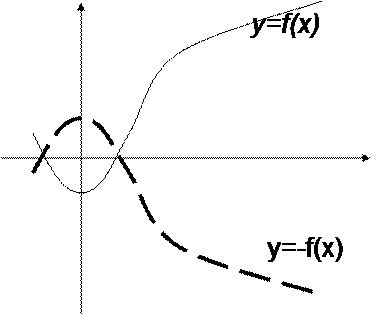
|
Значения тригонометрических функций
|
|
|
| a, рад | 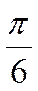
| 
| 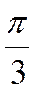
| 
| p | 
| |
| sin a | 
| 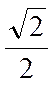
| 
| -1 | |||
| cos a | 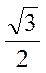
| 
| 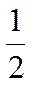
| -1 | |||
| tg a | 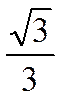
| 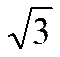
| ¾ | ¾ | |||
| ctg a | ¾ | 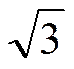
| 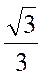
| ¾ |
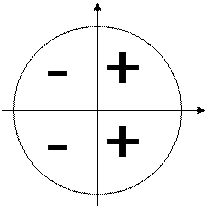

 Знаки тригонометрических функций
Знаки тригонометрических функций
|
| ||||
| |||||
Основные тригонометрические тождества
| sin²a + cos²a = 1 | tga× ctga= 1 |

| 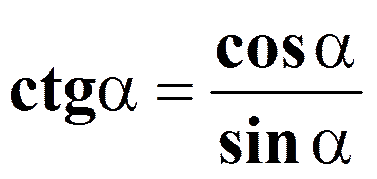
|
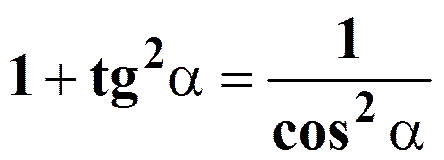
| 
|
Формулы сложения
sin( a+β ) = sin a cos β + cos a sin β
sin ( a-β ) = sin a cos β -cos a sin β
cos ( a+β ) = cos a cos β -sin a sin β
cos (a-β ) = cos a cos β + sin a sin β
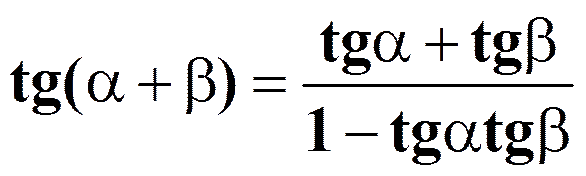
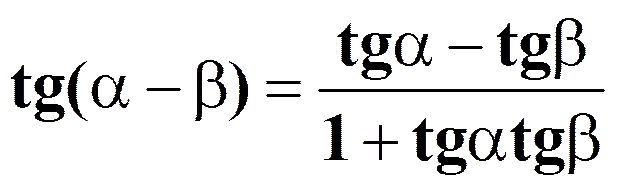
Формулы двойного аргумента
sin 2 a = 2 sin a cos a
cos 2 a =cos² a -sin² a =2 cos² a -1=1-2sin² a
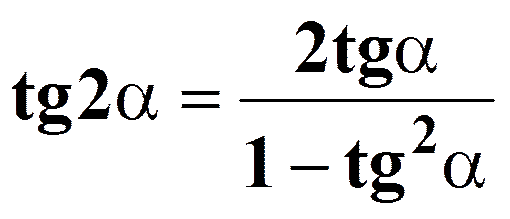
1+ cos 2 a = 2 cos² a 1-cos 2 a = 2 sin² a
Формулы половинного аргумента
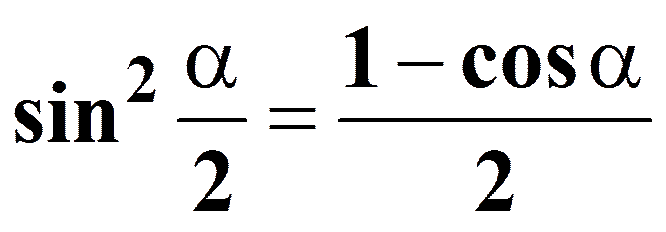

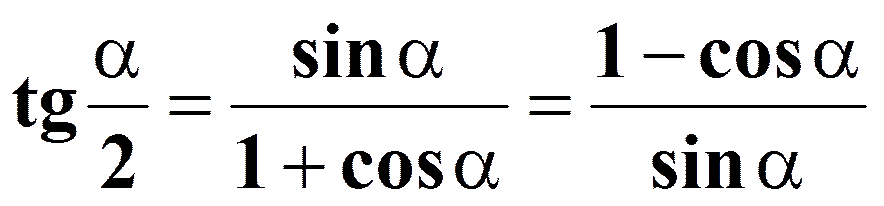
Формулы суммы

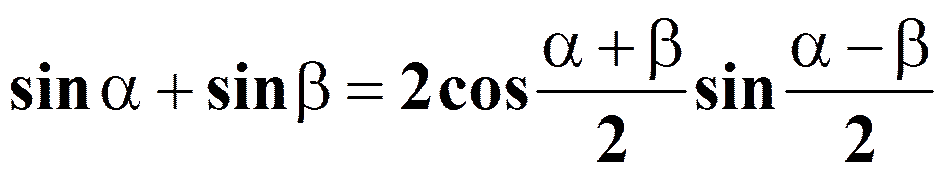
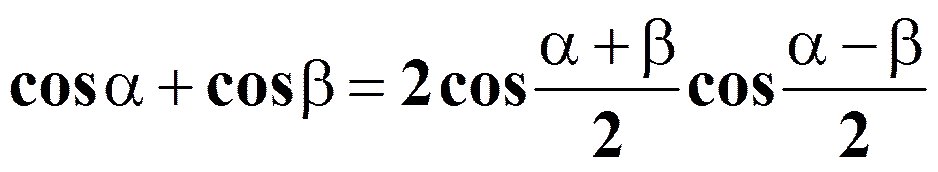

Формулы преобразования произведения в сумму
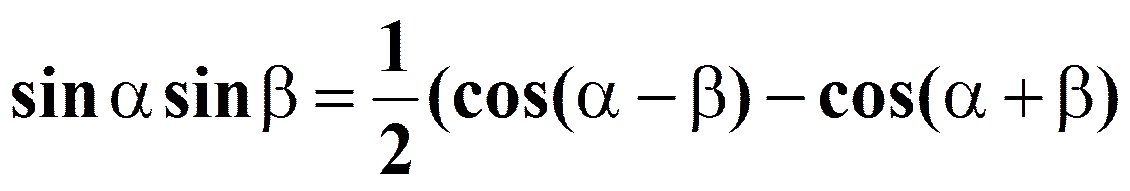
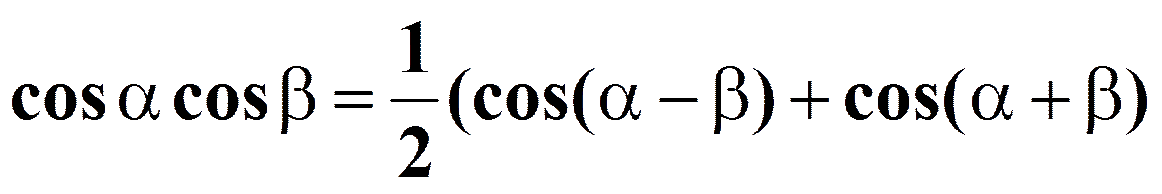

Тригонометрические уравнения
1. sin x = a, ½ a ½£1
x =(-1)n arcsin a +p n, n ÎZ
Частные случаи:
· sin x =1 x = 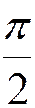 +2p n, nÎZ
· sin x = -1 x = +2p n, nÎZ
· sin x = -1 x = 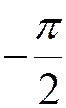 +2p n, nÎZ
· sin x =0 x = p n, nÎZ +2p n, nÎZ
· sin x =0 x = p n, nÎZ
| 2. cos x = a, ½ a ½£1
x =± arccos a +2p n, n ÎZ
Частные случаи:
· cos x =1 x= 2p n, n ÎZ
· cos x = -1 x = p+2p n, nÎZ
· cos x =0 x = 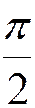 +p n, nÎZ +p n, nÎZ
|
| 3. tg x = a x = arctg a +p n, n ÎZ | Связь градусной и радианной мер:
a °= 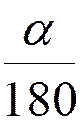 ×p (радиан)
x (радиан)= ×p (радиан)
x (радиан)= 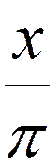 ×180° ×180°
|
Степени
 · с натуральным показателем: a 1= a, a n = a×a×…×a, nÎN, aÎR
· с натуральным показателем: a 1= a, a n = a×a×…×a, nÎN, aÎR
n раз
· с целым показателем: a 0=1; a -n= 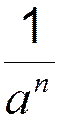 , nÎN, aÎR, a¹0
, nÎN, aÎR, a¹0
|
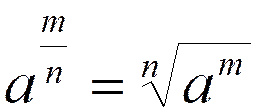 , mÎZ, nÎN,
, mÎZ, nÎN,
Свойства степеней
| 1. a p× a r= a p+r | 3. a r× b r=(ab)r | 5. (a p)r= a pr | |||
2. 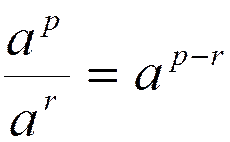
| 4. 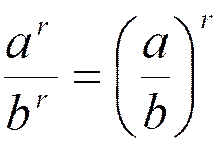
| 6. 
| |||
| 7. Если a > b ³0 и | r>0, то a r> b r | 8. Если p>r и | a >1, то a p> a r | ||
| r<0, то a r< b r | 0< a <1, то a r< b r | ||||
Логарифм и его свойства
Определение:log ba=x (a>0,b>0, b¹1): bx=a
Основное логарифмическое тождество: 
Свойства:
1. log a a =1
2. log a 1=0
3. log a bp = p log a b
4. log a (bc)= log a b +log a c
5. log a (b/c)= log a b -log a c
6. 
| Дополнительные соотношения:
1.  2.
2.  3. log n b ×log m c =log m b ×log n c
4.
3. log n b ×log m c =log m b ×log n c
4. 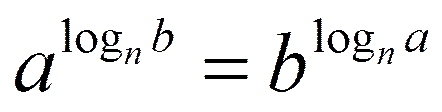
|
Построение графика квадратичной функции
|
|
|
y=ax2+bx+c
График – парабола, направление ветвей.
2. xв= 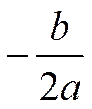 ; yв= ax2+bx+c=0
; yв= ax2+bx+c=0
(xв; yв) – вершина параболы.
3. x= xв – ось симметрии
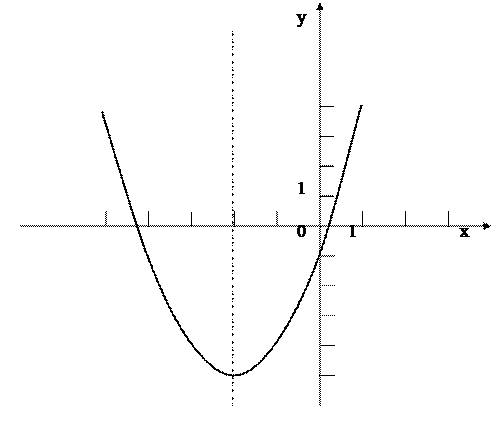 4. Таблица значений
4. Таблица значений
Пример: Построить график функции y=x2+4x-1.
1. График – парабола. Ветви направлены вверх
2. 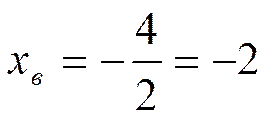 ; yв =(-2)2+4×(-2) -1=4-8-1= -5
; yв =(-2)2+4×(-2) -1=4-8-1= -5
(-2; -5) – вершина параболы
3. x= -2 – ось симметрии
4.
| x | -5 | -4 | -3 | -2 | -1 | ||
| y | -1 | -4 | -5 | -4 | -1 |
Преобразование графика квадратичной функции
· y=ax2+n
 1. График – парабола, направление ветвей.
1. График – парабола, направление ветвей.
N) – вершина параболы (сдвиг вдоль оси y)
Пример 1: Построить график функции y=x2-4.
1. График – парабола, ветви направлены вверх
2. (0; -4) – вершина параболы
Пример 2: Построить график функции y=-2x2+3.
1. График – парабола, ветви направлены вниз
2. (0; 3) – вершина параболы
 · y=a(x-m)2
· y=a(x-m)2
График – парабола, направление ветвей.
m; 0) – вершина параболы (сдвиг вдоль оси x)
Пример 1: Построить график функции y=(x-2)2.
1. График – парабола, ветви направлены вверх
2. (2; 0) – вершина параболы
Пример 2: Построить график функции y=½(x+1)2.
1. График – парабола, ветви направлены вниз
2. (-1; 0) – вершина параболы
|
|
|