 |
Динамика материальной точки. Импульс силы, импульс тела. Законы Ньютона.
|
|
|
|
Кинематика поступательного движения
При поступательном движении тела все точки тела движутся одинаково, и, вместо того чтобы рассматривать движение каждой точки тела, можно рассматривать движение только одной его точки.
Основные характеристики движения материальной точки: траектория движения, перемещение точки, пройденный ею путь, координаты, скорость и ускорение.
Линию, по которой движется материальная точка в пространстве, называют траекторией.
Перемещением материальной точки за некоторый промежуток времени называется вектор перемещения ∆r=r-r0, направленный от положения точки в начальный момент времени к ее 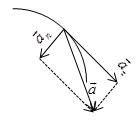 положению в конечный момент.
положению в конечный момент.
Скорость материальной точки представляет собой вектор, характеризующий направление и быстроту перемещения материальной точки относительно тела отсчета. Вектор ускорения характеризует быстроту и направление изменения скорости материальной точки относительно тела отсчета.
Ускорение – это величина, равная отношению изменения скорости движения тела к длительности промежутка времени, за которое это изменение скорости произошло. Среднее ускорение на основе этого определения равно, м/с²:

3)Тангенциальная и нормальная составляющие ускорения.
 - тангенциальная составляющая ускорения направлена по касательной к траектории точки и равна
- тангенциальная составляющая ускорения направлена по касательной к траектории точки и равна

где вектор 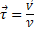 – единичный вектор касательной, проведенной в точке траектории и направлении скорости
– единичный вектор касательной, проведенной в точке траектории и направлении скорости 
Векторы  и
и 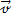 сонаправлены при равноускоренном движении;
сонаправлены при равноускоренном движении;  при
при  т.е. при равнозамедленном движении.
т.е. при равнозамедленном движении.
Касательное ускорение  - характеризует быстроту изменения модуля вектора скорости точки (характеризует изменение скорости по величине).
- характеризует быстроту изменения модуля вектора скорости точки (характеризует изменение скорости по величине).
|
|
|
Для равномерного движения:
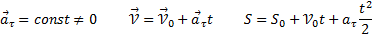
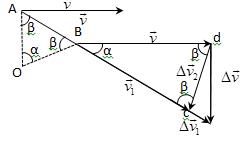
 -нормальная составляющая ускорения (нормальное ускорение) направлена по нормали к траектории и рассматриваемой точке в сторону к центру кривизны траектории. Криволинейную траекторию можно представить как совокупность элементарных участков, каждый из которых может рассматриваться как дуга окружности некоторого радиуса R (называемого радиусом кривизны кривой в окружности данной точки траектории)
-нормальная составляющая ускорения (нормальное ускорение) направлена по нормали к траектории и рассматриваемой точке в сторону к центру кривизны траектории. Криволинейную траекторию можно представить как совокупность элементарных участков, каждый из которых может рассматриваться как дуга окружности некоторого радиуса R (называемого радиусом кривизны кривой в окружности данной точки траектории)
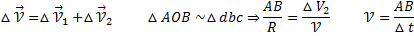
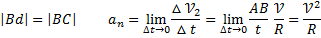
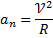
Нормальное ускорение характеризует быстроту изменения направления вектора скорости (характеризует изменение скорости по направлению).
Модуль полного ускорения:
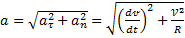
Классификация движений зависит от тангенциальных и нормальных составляющих:
1) 
2) 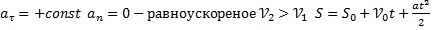
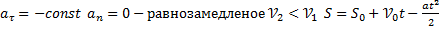
3) 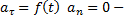
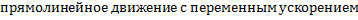
4) 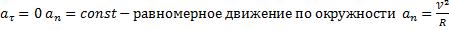
5) 
6) 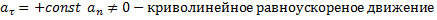
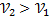

7) 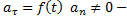
Кинематика вращательного движения вокруг неподвижной оси. Соотношения между характеристиками поступательного и вращательного движения
При вращательном движении вокруг неподвижной оси z (рис. 3) тело имеет одну степень свободы; его положение определяется углом поворота φ, а закон движения задаётся уравнением φ = f (t). Основными кинематическими характеристиками являются угловая скорость ω=dφ/dt и угловое ускорение ε = dω/dt тела. Величины ω и ε изображаются в виде векторов, направленных вдоль оси вращения. Зная ω и ε, можно определить скорость и ускорение любой точки тела.

Величины, характеризующие поступательное и вращательное движение и связь между ними:
| Поступательное движение | Вращательное движение | Связь | |
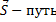
| 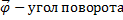
| 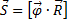
| |
 -cкорость; -cкорость;
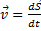
|  ω= ω= 
| 
| |
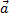 -ускорение; -ускорение; 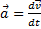
| 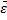 – угловое ускорение – угловое ускорение
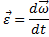
| 
| |
| m-масса | 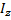 - момент инерции - момент инерции
| 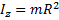
| |
 -uмпульс; -uмпульс;
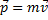
| 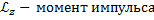
| 
| |
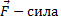 ; ;

| 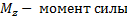
| 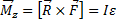
| |
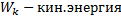 ; ;
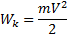
| 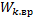 – кин. энергия вращательного движения – кин. энергия вращательного движения
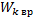 = = 
| ||
dA-элементарная работа;
dA= 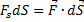
| dA элементарная работа вращательного движения | dA= 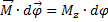
|
Динамика материальной точки. Импульс силы, импульс тела. Законы Ньютона.
|
|
|
§1 Первый закон Ньютона
Инерциальные системы отсчета
1-й закон Ньютона: всякое тело находится в состоянии покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не выведет его из этого состояния.
 - I закон Ньютона
- I закон Ньютона
Этот закон называют законом инерции. Инерция - способность тела сохранять скорость. Движение по инерции - движение с постоянной скоростью.
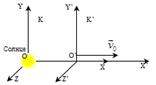 1-й закон Ньютона выполняется не во всех системах отсчета. Системы отсчета, в которых выполняется 1-й закон Ньютона, называются инерциальными. Любая система отсчета, движущаяся относительно некоторой инерциальной системы прямолинейно и равномерно, будет также инерциальной.
1-й закон Ньютона выполняется не во всех системах отсчета. Системы отсчета, в которых выполняется 1-й закон Ньютона, называются инерциальными. Любая система отсчета, движущаяся относительно некоторой инерциальной системы прямолинейно и равномерно, будет также инерциальной.
Примером инерциальной системы отсчета может служить гелиоцентрическая система отсчета, т. е. система отсчета, связанная с Солнцем.
Любая система отсчета, движущаяся относительно гелиоцентрической равномерно и прямолинейно будет являться инерциальной.
Лабораторная система отсчета, оси координат которой жестко связаны с Землей, неинерциальная из-за суточного вращения Земли. Однако вращение Земли происходит очень медленно с а=0,034 м/с2, и поэтому в большинстве задач лабораторную систему отсчета можно приближенно считать инерциальной.
Содержание 1-го з. Н. сводится к двум утверждениям:
1) все тела обладают свойством инертности;
2) существуют инерциальные системы отсчета.
Инерциальные системы отсчета играют особую роль не только в механике, но и в других разделах физики, т. к. согласно принципу относительности Эйнштейна математическая запись любого физического закона должна иметь один и тот же вид во всех инерциальных системах отсчета..
2-й закон Ньютона
Одинаковое воздействие по-разному изменяет движение различных тел. При воздействии всякое тело изменяет свою скорость не сразу, а постепенно. Способность тела сохранять свою скорость называется инертностью. Мерой инертностью является масса. Масса тела – положительная скалярная величина, являющаяся мерой инертности тела, т. е. характеризует способность тела сохранять свою скорость.
Под действием силы тело изменяет свою скорость не мгновенно, а постепенно, т. е. приобретает конечное ускорение, которое тем меньше, чем больше масса, т. е. при воздействии одной и той же силы  .
.
|
|
|
Плотность тела ровна отношению массы dm малого объёма 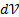 к величине этого объёма
к величине этого объёма 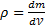 , если тело однородно, то
, если тело однородно, то  и
и  .
.
Центром инерции, или центром масс, системы материальных точек называется точка С радиус-вектор  , который равен
, который равен
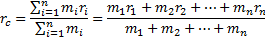
Векторная величина 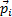 равная произведению массы m материальной точки на ее скорость называется импульсом (или количеством движения) этой материальной точки
равная произведению массы m материальной точки на ее скорость называется импульсом (или количеством движения) этой материальной точки
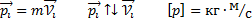
Импульсом системы материальных точек называется вектор 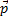 , равный геометрической сумме (т. е. сумме векторов) всех материальных точек
, равный геометрической сумме (т. е. сумме векторов) всех материальных точек
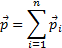
Скорость центра инерции:
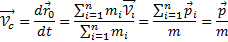
т. е. импульс системы равен произведению массы всей системы на скорость ее центра инерции:
2-й закон Ньютона: скорость изменения импульса тела равна действующей на тело силе F
 - 2-й закон Ньютона
- 2-й закон Ньютона
Если на тело действует несколько сил, то под силой F во втором законе Ньютона нужно понимать равнодействующую силу - геометрическую сумму всех сил, действующих на тело.
Из второго закона Ньютона следует, что 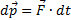
Векторная величина Fdt называется элементарным импульсом силы.
Импульс силы за конечный промежуток времени t2-t1 равен 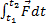 , где
, где 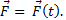
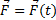

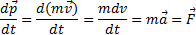
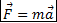
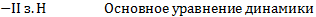
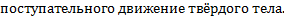
Сила, действующая на тело, равна произведению массы тела на его ускорение

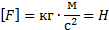
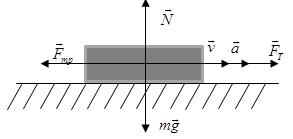

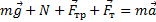
x: 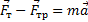
y: -mg + N=0
Касательное и нормальное ускорение определяются соответствующими составляющими силы F
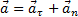
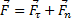

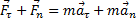
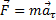

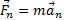

Сила Fn, сообщающая точке нормальное ускорение, направлена к центру кривизны траектории и потому называется центростремительной силой.
6) Преобразования Галилея. Инвариантность законов Ньютона к преобразованиям Галилея, закон сложения скоростей
корости частиц соответственно в системах 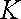


 и
и 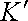

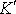
 . Полученная формула (3.15) выражает закон векторного сложения скоростей.
. Полученная формула (3.15) выражает закон векторного сложения скоростей.
Дифференцируя (3.15) по времени, получим преобразование ускорений:






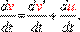
 (3.17)
(3.17)
Поскольку системы 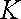


 и
и 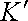

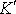
 инерциальные, то
инерциальные, то 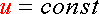


 , благодаря чему
, благодаря чему 

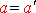
 , (3.18)
, (3.18)
где 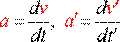
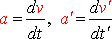
- ускорения частиц соответственно в системах 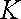


 и
и 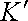

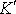
 . Следовательно, ускорение инвариантно относительно преобразований Галилея.
. Следовательно, ускорение инвариантно относительно преобразований Галилея.
|
|
|
Покажем, инвариантность также относительной скорости двух частиц, т.е. скорости одной частицы относительно системы отсчета, связанной с другой.
Пусть частицы 1 и 2 имеют в системах отсчета 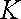


 и
и 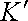

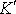
 соответственно скорости
соответственно скорости 


 и
и 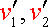

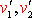
 . Согласно векторному закону сложения скоростей (3.15)
. Согласно векторному закону сложения скоростей (3.15)


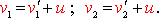

Скорость частицы 2 относительно частицы 1 будет:
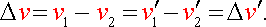

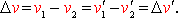

Следовательно,
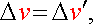

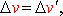
 (3.19)
(3.19)
- относительная скорость одинакова во всех системах отсчета.
Отметим, что все формулы, приведенные в данном параграфе, верны и в случае 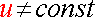


 , за исключением формулы (3.18).
, за исключением формулы (3.18).
Теперь покажем, что уравнение, выражающее второй закон Ньютона, инвариантно относительно преобразований Галилея, поскольку не зависит от начальных условий движения. Запишем второй закон Ньютона в инерциальных системах 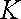


 и
и 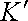

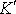
 :
:




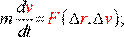


 (3.20)
(3.20)
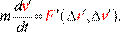

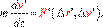
 (3.20')
(3.20')
Так как ньютоновская масса частицы независима от состояния движения, а ускорение, как мы видели, инвариантная величина, то левая часть второго закона Ньютона инвариантна относительно преобразований Галилея. Мы знаем, что сила зависит от относительного положения 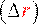


 тел и относительной скорости
тел и относительной скорости 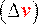


 этих тел, которые также величины инвариантные.
этих тел, которые также величины инвариантные. 


 Функции, состоящие только из инвариантных величин, также инвариантны.
Функции, состоящие только из инвариантных величин, также инвариантны.
Итак, уравнение, выражающее второй закон Ньютона – Галилей-инвариантное уравнение.
Пусть частица совершает свободное падение в системе 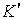 . Понятно, что в
. Понятно, что в 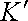

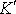
 закон движения частицы имеет вид
закон движения частицы имеет вид 





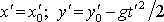
 , (3.21)
, (3.21)
где величины 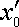


 ,
, 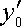


 – координаты начального положения частицы в
– координаты начального положения частицы в 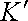

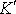
 . Положение частицы в момент
. Положение частицы в момент 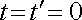


 в
в 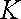


 характеризуется теми же координатами
характеризуется теми же координатами 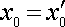

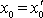
 и
и 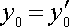

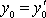
 , поскольку, согласно нашему выбору, в начальный момент системы отсчета
, поскольку, согласно нашему выбору, в начальный момент системы отсчета 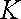


 и
и 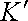

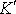
 совпадают. Однако, благодаря движению системы
совпадают. Однако, благодаря движению системы 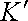

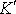
 , частица будет иметь относительно
, частица будет иметь относительно 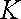


 начальную скорость
начальную скорость 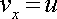

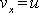
 .
.
Следовательно, закон движения частицы в К есть: 


 . (3.22)
. (3.22)
Нетрудно проверить, что преобразования Галилея (3.13) с учетом условий 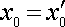

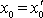
 и
и 

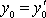
 приводят закон движения (3.20) к виду (3.20'). Таким же образом преобразования (3.14) приводят (13.20') к виду (3.20), как того и требует принцип относительности.
приводят закон движения (3.20) к виду (3.20'). Таким же образом преобразования (3.14) приводят (13.20') к виду (3.20), как того и требует принцип относительности.
7)) Обобщение 2 закона Ньютона на замкнутую механическую систему мат. точек. Понятие замкнутой системы, центра масс, закон движения центра масс. Другая форма записи второго закона Ньютона
Обозначим через 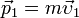 импульс материальной точки в начальный момент интервала Δt, а через
импульс материальной точки в начальный момент интервала Δt, а через 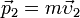 — импульс в конечный момент этого интервала. Тогда
— импульс в конечный момент этого интервала. Тогда 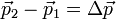 есть изменение импульса за время Δt. Теперь уравнение (1) можно записать так:
есть изменение импульса за время Δt. Теперь уравнение (1) можно записать так:
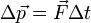 . (3)
. (3)
Так как Δt > 0, то направления векторов 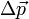 и
и  совпадают.
совпадают.
Согласно формуле (3)
изменение импульса материальной точки пропорционально приложенной к ней силе и имеет такое же направление, как и сила.
Именно так был впервые сформулирован второй закон Ньютона.
Произведение силы на время ее действия называют импульсом силы. Не надо путать импульс  материальной точки и импульс силы
материальной точки и импульс силы  . Это совершенно разные понятия.
. Это совершенно разные понятия.
Уравнение (3) показывает, что одинаковые изменения импульса материальной точки могут быть получены в результате действия большой силы в течение малого интервала времени или малой силы за большой интервал времени. Когда вы прыгаете с какой-то высоты, то остановка вашего тела происходит за счет действия силы со стороны земли или пола. Чем меньше продолжительность столкновения, тем больше тормозящая сила. Для уменьшения этой силы надо, чтобы торможение происходило постепенно. Вот почему при прыжках в высоту спортсмены приземляются на мягкие маты. Прогибаясь, они постепенно тормозят спортсмена. Формула (3) может быть обобщена и на тот случай, когда сила меняется во времени. Для этого весь промежуток времени Δt действия силы надо разделить на столь малые интервалы Δti, чтобы на каждом из них значение силы без большой ошибки можно было считать постоянным. Для каждого малого интервала времени справедлива формула (3). Суммируя изменения импульсов за малые интервалы времени, получим:
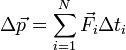 . (4)
. (4)
Символ Σ (греческая буква «сигма») означает «сумма». Индексы i = 1 (внизу) и N (наверху) означают, что суммируется N слагаемых.
Для нахождения импульса тела поступают так: мысленно разбивают тело на отдельные элементы (материальные точки), находят импульсы полученных элементов, а потом их суммируют как векторы.
Импульс тела равен сумме импульсов его отдельных элементов.
|
|
|
8) З акон сохранения импульса Справедливость закона сохранения импульса можно показать для замкнутой системы, состоящей из двух тел, применяя второй и третий законы Ньютона. Пусть первое тело, имеющее массу m1, движется со скоростью V1, второе тело, масса которого m2, движется со скоростьюV2.
При столкновении тела взаимодействуют друг с другом, и, согласно Третьему закону Ньютона, сила F12 =-F21, по второму закону Ньютона силаF12, действующая на первое тело,  изменит импульс первого тела, можно записать
изменит импульс первого тела, можно записать 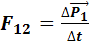 , точно так же можно записать, что сила F21 изменит импульс второго тела:
, точно так же можно записать, что сила F21 изменит импульс второго тела:  . Подставим значения F12 и F21 в третий закон Ньютона:
. Подставим значения F12 и F21 в третий закон Ньютона:  , т.к. время взаимодействия
, т.к. время взаимодействия 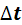 - одно и то же, то:
- одно и то же, то: 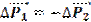 или
или  .
.
Рассматриваемая нами замкнутая система состояла из двух тел, полный вектор импульса этой системы 

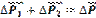 - это изменение вектора полного импульса. При взаимодействии двух тел получили, что изменение вектора полного импульса
- это изменение вектора полного импульса. При взаимодействии двух тел получили, что изменение вектора полного импульса 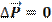 , следовательно, полный вектор импульса системы при взаимодействии не изменился: если
, следовательно, полный вектор импульса системы при взаимодействии не изменился: если 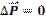 , то P = const.
, то P = const.
Если система состоит из N тел, то P = m1∙v1 + m2∙v2 +........+ mN∙vN есть полный вектор импульса замкнутой системы, и P = const.
Закон сохранения импульса (ЗСИ).
9) Работа. Мощность. Консервативные и неконсервативные силы.
Консервативные и неконсервативные силы
Консервативными силами называются силы, работа которых не зависит от пути перехода тела или системы из начального положения в конечное.
Характерное свойство таких сил – работа на замкнутой траектории равна нулю:
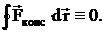
К консервативным силам относятся: сила тяжести, гравитационная сила, сила упругости и другие силы.
Неконсервативными силами называются силы, работа которых зависит от пути перехода тела или системы из начального положения в конечное.
Работа этих сил на замкнутой траектории отлична от нуля. К неконсервативным силам относятся: сила трения, сила тяги и другие силы.
Механической работой А называют скалярную величину, равную произведению модуля силы F, действующей на тело, и модуля перемещения s, совершаемого телом в направлении действия этой силы, т. е.
А=Fs. (3.9)
В случае, описываемом формулой (3.9), направление перемещения тела совпадает с направлением силы. Однако чаще встречаются случаи, когда сила и перемещение составляют между собой угол, не равный нулю или p. (рис. 30)
Разложим силу F на две взаимно перпендикулярные составляющие F1 и F2 (F=F1+F2). Поскольку механическая работа - величина скалярная, то работа силы F равна алгебраической сумме работ сил F1 и F2, т. е. А=А1+А2.
Под действием силы F2 тело перемещения не совершает, так как F2^s. Поэтому A2=0. Следовательно, работа А=А1=F1s. Из рисунка видно, что F1=Fcosa. Поэтому
А=Fsсоsa. (3.10)
имеет наименование джоуль (Дж):
1 Дж = 1Н·1м.
Мощность
Мощностью N называют величину, равную отношению работы А к промежутку времени t, в течение которого эта работа была совершена:N=A/t (3.11)
Из формулы (3.11) следует, что в СИ единицей мощности яв-ляется 1 Дж/с (джоуль в секунду). Эту единицу иначе называют ватт (Вт), 1 Вт= 1 Дж/с.
Связь между мощностью и скоростью при равномерном движении найдем, подставив (3.10) в (3.11):
N=Fvcosa.
(Эта формула справедлива и для переменного движения, если под N понимать мгновенную мощность, а под V - мгновенную скорость). Если направление силы совпадает с направлением перемещения, то cosa=1 и N=Fv. Из последней формулы следует, что
F=N/v и v=N/F.
Из этих формул видно, что при постоянной мощности двигателя скорость движения обратно пропорциональна силе тяги и наоборот. На этом основан принцип действия коробки скоростей (коробки перемены передач) различных транспортных средств.
|
|
|


