 |
Оценочные средства по дисциплине «Математика»
|
|
|
|
Контроль и оценка результатов освоения дисциплины осуществляется преподавателем в процессе проведения практических занятий, а также выполнения обучающимися индивидуальных заданий.
| Результаты обучения (личностные, метапредметные) | Коды формируемых профессиональных и общих компетенций | Формы и методы контроля и оценки результатов обучения |
| 1 | 2 | 3 |
| Личностные | ||
| Сформированность представлений о математике как универсальном языке науки, средстве моделирования явлений и процессов, идеях и методах математики | ОК 02. Осуществлять поиск, анализ и интерпретацию информации, необходимой для выполнения задач профессиональной деятельности ОК 04. Работать в коллективе и команде, эффективно взаимодействовать с коллегами, руководством, клиентами | Деловая игра «Математика вокруг нас» |
| Понимание значимости математики для научно-технического прогресса, сформированность отношения к математике как к части общечеловеческой культуры через знакомство с историей развития математики, эволюцией математических идей | ОК 01. Выбирать способы решения задач профессиональной деятельности применительно к различным контекстам ОК 05. Осуществлять устную и письменную коммуникацию на государственном языке Российской Федерации с учетом особенностей социального и культурного контекста | Рефераты на темы «История развития математики», «Великие ученые-математики», «Роль математики в нашей профессии». |
| Развитие логического мышления, пространственного воображения, алгоритмической культуры, критичности мышления на уровне, необходимом для будущей профессиональной деятельности, для продолжения образования и самообразования | ОК 02. Осуществлять поиск, анализ и интерпретацию информации, необходимой для выполнения задач профессиональной деятельности ОК 03. Планировать и реализовывать собственное профессиональное и личностное развитие | Практические задания по темам: «Признаки монотонности функции», «Нахождение экстремальных значений функции», «Точки перегиба. Направление выпуклости графика функции», «Применение производной к исследованию функций и построению графиков». Контрольная работа №8 |
| Овладение математическими знаниями и умениями, необходимыми в повседневной жизни, для освоения смежных естественно-научных дисциплин и дисциплин профессионального цикла, для получения образования в областях, не требующих углубленной математической подготовки; | ОК 09. Использовать информационные технологии в профессиональной деятельности | Оценка выполнения проверочной работы по теме: «Интеграл и его практическое применение в геометрии и физике». Математический диктант. Проектная работа на тему «Применение интеграла при вычислении физических величин, площадей» Контрольная работа №9 Решение задач на вычисление площадей поверхности многогранников и тел вращения. Контрольная работа №7 |
| Готовность и способность к образованию, в том числе самообразованию, на протяжении всей жизни; сознательное отношение к непрерывному образованию как условию успешной профессиональной и общественной деятельности | ОК 01. Выбирать способы решения задач профессиональной деятельности применительно к различным контекстам ОК 02. Осуществлять поиск, анализ и интерпретацию информации, необходимой для выполнения задач профессиональной деятельности | Практические задания по темам «Методы решения тригонометрических уравнений», «Простейшие тригонометрические неравенства», «Решение тригонометрических неравенств», «Простейшие преобразования графиков (графическая работа)». Контрольная работа № 6 |
| Готовность и способность к самостоятельной творческой и ответственной деятельности; | ОК 04. Работать в коллективе и команде, эффективно взаимодействовать с коллегами, руководством, клиентами | Исследовательская работа: «Роль математики в моей профессии» |
| Готовность к коллективной работе, сотрудничеству со сверстниками в образовательной, общественно полезной, учебно-исследовательской, проектной и других видах деятельности; | ОК 04. Работать в коллективе и команде, эффективно взаимодействовать с коллегами, руководством, клиентами ОК 07. Содействовать сохранению окружающей среды, ресурсосбережению, эффективно действовать в чрезвычайных ситуациях | Математическая игра: «Повторяем интегралы» |
| Отношение к профессиональной деятельности как возможности участия в решении личных, общественных, государственных, общенациональных проблем; | ОК 06. Проявлять гражданско-патриотическую позицию, демонстрировать осознанное поведение на основе традиционных общечеловеческих ценностей | Решение ситуационных задач по теме: «Понятие о задачах математической статистики. Решение практических задач с применением вероятностных методов» Контрольная работа №11 |
| метапредметные | ||
| Умение самостоятельно определять цели деятельности и составлять планы деятельности; самостоятельно осуществлять, контролировать и корректировать деятельность; использовать все возможные ресурсы для достижения поставленных целей и реализации планов деятельности; выбирать успешные стратегии в различных ситуациях; | ОК 02. Осуществлять поиск, анализ и интерпретацию информации, необходимой для выполнения задач профессиональной деятельности ОК 03. Планировать и реализовывать собственное профессиональное и личностное развитие | Оценка результатов деятельности обучающихся при выполнении проверочных работ по теме. Оценка результатов деятельности обучающихся при выполнении домашних работ по теме. Самоконтроль и (или) взаимоконтроль тестирования по теме. |
| Готовность и способность к самостоятельной информационно-познавательной деятельности, включая умение ориентироваться в различных источниках информации, критически оценивать и интерпретировать информацию, получаемую из различных источников; | ОК 02. Осуществлять поиск, анализ и интерпретацию информации, необходимой для выполнения задач профессиональной деятельности ОК 03. Планировать и реализовывать собственное профессиональное и личностное развитие | Оценка результатов деятельности обучающихся при выполнении проверочных работ по теме. Оценка результатов деятельности обучающихся при выполнении домашних работ по теме. |
| Владение навыками познавательной рефлексии как осознания совершаемых действий и мыслительных процессов, их результатов и оснований, границ своего знания и незнания, новых познавательных задач и средств для их достижения; | ОК 03. Планировать и реализовывать собственное профессиональное и личностное развитие | Итоговый опрос учащихся по теме в конце урока. |
| Целеустремленность в поисках и принятии решений, сообразительность и интуиция, развитость пространственных представлений; способность воспринимать красоту и гармонию мира. | ОК 02. Осуществлять поиск, анализ и интерпретацию информации, необходимой для выполнения задач профессиональной деятельности. | Решение ситуационных задач по теме. Оценка тестирования по теме. |
| Предметные | ||
| Сформированность представлений о математике как части мировой культуры и месте математики в современной цивилизации, способах описания явлений реального мира на математическом языке | ОК 06. Проявлять гражданско-патриотическую позицию, демонстрировать осознанное поведение на основе традиционных общечеловеческих ценностей | Проект на тему”Применение показательной функции в науке, технике и жизни” |
| Сформированность представлений о математических понятиях как важнейших математических моделях, позволяющих описывать и изучать разные процессы и явления; понимание возможности аксиоматического построения математических теорий | ОК 01. Выбирать способы решения задач профессиональной деятельности применительно к различным контекстам ОК 02. Осуществлять поиск, анализ и интерпретацию информации, необходимой для выполнения задач профессиональной деятельности. | Проектная работа на тему «Изучение круговых движений, измерение углов на практике, измерение площади кругового сектора» Проектная работа на тему «Применение тригонометрии в технической механике» Контрольная работа №5 Проектная работа на тему «Из истории логарифмов» Контрольная работа №2 |
| - Владение методами доказательств и алгоритмов решения, умение их применять, проводить доказательные рассуждения в ходе решения задач; | ОК 03. Планировать и реализовывать собственное профессиональное и личностное развитие | Практические занятия: “Признаки взаимного расположения прямых.” “Угол между прямыми”. “Взаимное расположение прямых и плоскостей”. Контрольная работа №3 |
| - Владение стандартными приемами решения рациональных и иррациональных, показательных, степенных, тригонометрических уравнений и неравенств, их систем; использование готовых компьютерных программ, в том числе для поиска пути решения и иллюстрации решения уравнений и неравенств. | ОК 09. Использовать информационные технологии в профессиональной деятельности. ОК 01. Выбирать способы решения задач профессиональной деятельности применительно к различным контекстам ОК 02. Осуществлять поиск, анализ и интерпретацию информации, необходимой для выполнения задач профессиональной деятельности. | Тест. Контрольная работа №1. Контрольная работа №6 Практические занятия “Уравнение asinx + bcosx = c ” “Уравнения, решаемые разложением левой части на множители”. |
| - Cформированность представлений об основных понятиях математического анализа и их свойствах, владение умением характеризовать поведение функций, использование полученных знаний для описания и анализа реальных зависимостей | ОК 01. Выбирать способы решения задач профессиональной деятельности применительно к различным контекстам ОК 02. Осуществлять поиск, анализ и интерпретацию информации, необходимой для выполнения задач профессиональной деятельности. | Проектная работа на тему «Описание колебательных процессов в механике, электротехнике, (движение маятника, переменный ток)» Контрольная работа №7 Проектная работа на тему «Примеры применения интеграла в физике и геометрии» Контрольная работа №10 |
| - Владение основными понятиями о плоских и пространственных геометрических фигурах, их основных свойствах; сформированность умения распознавать геометрические фигуры на чертежах, моделях и в реальном мире; применение изученных свойств геометрических фигур и формул для решения геометрических задач и задач с практическим содержанием | ОК 09. Использовать информационные технологии в профессиональной деятельности. ОК 01. Выбирать способы решения задач профессиональной деятельности применительно к различным контекстам ОК 02. Осуществлять поиск, анализ и интерпретацию информации, необходимой для выполнения задач профессиональной деятельности. | Практические занятия “Вычисление объемов, площадей многогранников, тел вращения” Контрольная работа №6 Проектная работа на тему: ”Использование координат и векторов при решении математических и прикладных задач”. Контрольная работа №4 |
| - Сформированность представлений о процессах и явлениях, имеющих вероятностный характер, статистических закономерностях в реальном мире, основных понятиях элементарной теории вероятностей; умений находить и оценивать вероятности наступления событий в простейших практических ситуациях и основные характеристики случайных величин | ОК 03. Планировать и реализовывать собственное профессиональное и личностное решение. ОК 11. Использовать знания по финансовой грамотности, планировать предпринимательскую деятельность в профессиональной сфере. | Проектная работа на тему: “Средние значения и их применение в статистике” Практическое занятие “Представление числовых данных” Практическое занятие “Вычисление вероятностей” Контрольная работа №11. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Самостоятельная работа
Вариант 1
Решить уравнения:
1.  =
= 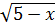
2.  =x-2
=x-2
3.  =4
=4
4.  =4+x
=4+x
5.  =1
=1
Вариант 2
1.  =
= 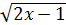
2.  =1-x
=1-x
3.  +
+ 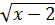 =9
=9
4. 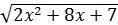 =x+2
=x+2
5.  =3
=3
Вариант 3
 =x-1
=x-1
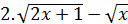 =1
=1
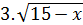 +
+  =6
=6
 -
-  =2
=2
 =x
=x
Контрольная работа №1
Вариант 1
1. Найдите значение выражения:
а) 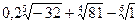
б) 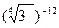
в) 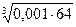
г) 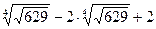
2. Упростите выражение:
a)  b) (y
b) (y 
 )
)  y
y 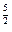
3. Представьте в виде обыкновенной дроби бесконечную десятичную дробь:
a) 0,(162) б) 0,8(4)
4. Упростите:
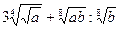
5. Упростите:
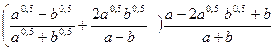
6. Сравнить числа:
1) 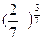 и
и  2)
2) 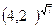 и
и 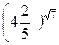
3)  и 1
и 1
7. Расположите в порядке возрастания числа:
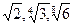
Вариант 2
1. Найдите значение выражения:
а) 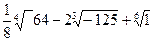
б) 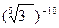
в) 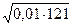
г) 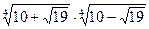
2. Упростите выражение:
a)  b) (y
b) (y  )
)  y
y 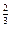
3. Представьте в виде обыкновенной дроби бесконечную десятичную дробь:
a) 0,(72) б) 0, (74)
4. Упростите:
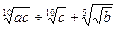
5. Упростите:
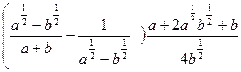
6. Сравнить числа:
1)  и
и  2)
2) 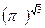 и
и 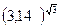
3) 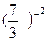 и 1
и 1
7. Расположите в порядке возрастания числа:
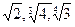

Вариант 3
1. Найдите значение выражения:
а)  б)
б)  в)
в) 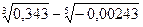
2. Упростите выражение:
a)  b) (x
b) (x  )
)  x
x 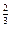
3. Представьте в виде обыкновенной дроби бесконечную десятичную дробь:
a) 0,4(5)
4. Упростите:
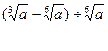
5. Сравнить числа:
1)  и 1
и 1
2)  и 1
и 1
3)  и
и 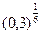
6. Расположите в порядке возрастания числа:
Самостоятельная работа
 Вариант 1
Вариант 1
1. Вычислить:
1) 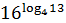
2) 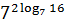
3) 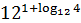
4) 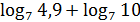
5) 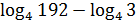
6) 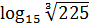
7) 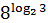
8) 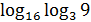
9)  +
+ 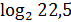
10) 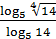
11) Зная, что 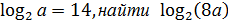
12) 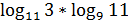
13) Решить уравнение:
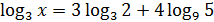
Вариант 2
1. Вычислить:
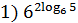
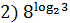
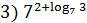
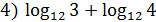
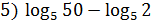
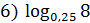
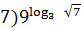
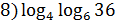
 +
+ 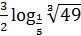
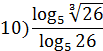
11)Зная, что 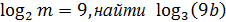
12) 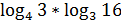
13)Решить уравнение:
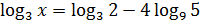
Вариант 3
1.Вычислить:
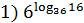
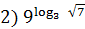
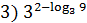
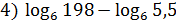
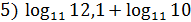
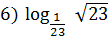
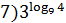
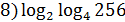
 +
+ 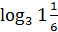
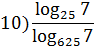
11) Зная, что 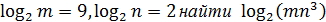
12) 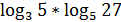
13) Решить уравнение:
 =14
=14
Контрольная работа №2
Вариант 1
1. Решить уравнения:
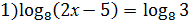
2) 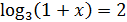
3) 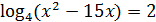
4) 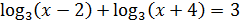
5) 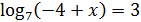
2. Решить неравенства:
1) 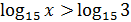
2) 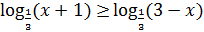
Вариант 2
1. Решить уравнения:
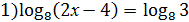
2) 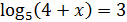
3) 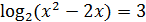
4) 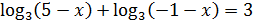
5) 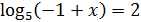
2. Решить неравенства:
1) 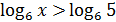
2) 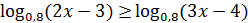
Вариант 3
1. Решить уравнения:
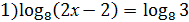
2) 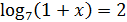
3)  =
= 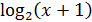
4) 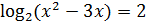
5) 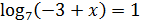
2. Решить неравенства:
1) 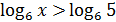
2) 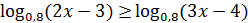
Вариант 4
1. Решить уравнения:
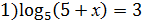
2) 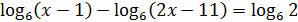
3) 
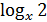 =3
=3
4) 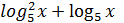 -2=0
-2=0
5) 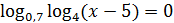
2. Решить неравенства:
1) 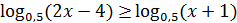
2) 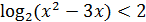
Вариант 5
1. Решить уравнения:
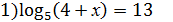
2) 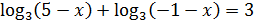
3) 
 =5
=5
4)  -3=0
-3=0
5) 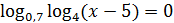
2. Решить неравенства: 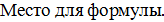
1) 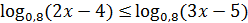
2) 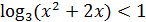
Контрольная работа №3
Вариант 1
1. В тетраэдре ABCD укажите прямую, скрещивающуюся с прямой AD.
2. В кубе ABCDA1B1C1D1 в плоскости ABCD найдите прямые, параллельные прямой B1 C1.
3. В кубе ABCDA1B1C1D1 найдите угол между скрещивающимися прямыми AA1 и BD.
4. Даны параллелограмм ABCD и трапеция ABEK с основанием EK, не лежащие в одной плоскости. Выясните взаимное расположение прямых CD и EK. Найдите периметр трапеции, если в нее можно вписать окружность и CD=22 см, EK=16 см.
5. Сумма всех ребер параллелепипеда ABCDA1B1C1D1 равна 120 см. Найдите длины ребер, если AB:BC:AA1= 4:5:6.
6. В тетраэдре ABCD:  DBC=
DBC=  DBA=
DBA=  ABC=90̊, BD=BA=BC=2 см. Найдите площадь грани ADC.
ABC=90̊, BD=BA=BC=2 см. Найдите площадь грани ADC.
Вариант 2
1. В тетраэдре ABCD укажите прямую, скрещивающуюся с прямой AB.
2. В кубе ABCDA1B1C1D1 в плоскости ABCD найдите прямые, параллельные прямой A1B1.
3. В кубе ABCDA1B1C1D1 найдите угол между скрещивающимися прямыми BB1 и AC.
4.Даны параллелограмм ABCD и трапеция ABEK с основанием EK, не лежащие в одной плоскости. Выясните взаимное расположение прямых CD и EK. Найдите периметр трапеции, если в нее можно вписать окружность и CD=20 см, EK=16 см.
5.Сумма всех ребер параллелепипеда ABCDA1B1C1D1 равна 144 см. Найдите длины ребер, если AB:BC:AA1= 2:3:4.
6. В тетраэдре ABCD:  DBC=
DBC=  DBA=
DBA=  ABC=60̊, BD=BA=BC=4 см. Найдите площадь грани ADC.
ABC=60̊, BD=BA=BC=4 см. Найдите площадь грани ADC.
Вариант 3
1. В тетраэдре ABCD укажите прямую, скрещивающуюся с прямой BC.
2. В кубе ABCDA1B1C1D1 найдите прямые, параллельные прямой D D1.
3.В кубе ABCDA1B1C1D1 в плоскости ABCD найдите угол между скрещивающимися прямыми AD и BB1.
4.Даны параллелограмм ABCD и трапеция ABEK с основанием EK, не лежащие в одной плоскости. Выясните взаимное расположение прямых CD и EK. Найдите периметр трапеции, если в нее можно вписать окружность и CD=30 см, EK=12 см.
5.Сумма всех ребер параллелепипеда ABCDA1B1C1D1 равна 88 см. Найдите длины ребер, если AB:BC:AA1= 2:4:5.
Вариант 4
1. В тетраэдре ABCD укажите прямую, скрещивающуюся с прямой DB.
2. В кубе ABCDA1B1C1D1 найдите прямые, параллельные прямой CC1.
3.В кубе ABCDA1B1C1D1 в плоскости ABCD найдите угол между скрещивающимися прямыми AD и B1C.
4.Даны параллелограмм ABCD и трапеция ABEK с основанием EK, не лежащие в одной плоскости. Выясните взаимное расположение прямых CD и EK. Найдите периметр трапеции, если в нее можно вписать окружность и CD=30 см, EK=18 см.
5.Сумма всех ребер параллелепипеда ABCDA1B1C1D1 равна 168 см. Найдите длины ребер, если AB:BC:AA1= 3:5:6.
Контрольная работа №4
Вариант №1.
1. Найти длину вектора  , если А(3;4;1) В(0;-3;4)
, если А(3;4;1) В(0;-3;4)
2. 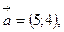
 . Найти координаты вектора
. Найти координаты вектора  .
.
3. Найти  , если
, если  ,
, 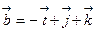
4. 
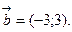 . Найти угол между ними.
. Найти угол между ними.
5.
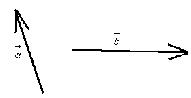
Построить вектор 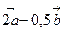
Вариант №2.
1. Найти длину вектора  , если С (3;1;0), В(8;4;0)
, если С (3;1;0), В(8;4;0)
2. 
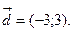 Найти координаты вектора
Найти координаты вектора 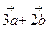
3. Найти  если
если  ,
,  .
.
4. 
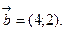 . Найти угол между ними.
. Найти угол между ними.
5.
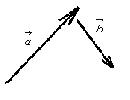
Построить вектор 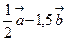
Вариант №3.
1. Найти длину вектора 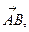 если А (-4;2;0), В(1;-8;2)
если А (-4;2;0), В(1;-8;2)
2. 
 Найти координаты вектора
Найти координаты вектора 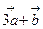
3. Найти 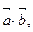 если
если 
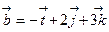
4. 
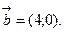 Найти угол между ними.
Найти угол между ними.
5.
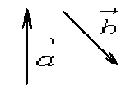
Построить вектор 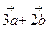
Вариант №4.
1. Найти длину вектора 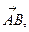 если А (4;5;2), В(7;-1;-8)
если А (4;5;2), В(7;-1;-8)
2.  Найти координаты вектора
Найти координаты вектора 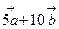
3. Найти 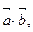 если
если 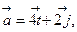
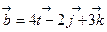
4. 
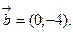 Найти угол между ними.
Найти угол между ними.
5.

Построить вектор 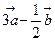
Контрольная работа №5
Вариант 1
1. Вычислить:
а) sin 33̊ 30´cos56̊ 30´ + sin 56̊ 30´ cos33̊ 30´
б) сos34̊ cos11̊ - sin 34̊ sin11̊
в) sin  cos
cos  -sin
-sin  cos
cos 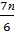
г) cos  cos
cos 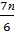 +sin
+sin  sin
sin 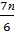
д) 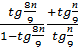
2. Вычислить, представив аргумент в виде суммы или разности:
а) sin105̊
б) cos120̊
в) tg 15̊
3. Вычислить:
а) sin(-  ) +3cos
) +3cos  +6sin
+6sin 
б) 2sin  +4sin
+4sin  +tg(-
+tg(-  )
)
в) 2sin 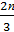 – ctg
– ctg 
г) 2cos  +tg
+tg 
4. Упростить выражение:
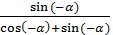 +
+ 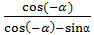
5. Вычислить:
а) sin α, если cosα= 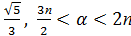
б) cosα и tg α, если sinα = -  , п
, п 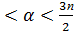
в) существует ли угол, для которого выполняется sinα= 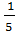 , cosα =
, cosα = 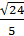
Вариант 2
1. Вычислить:
а) sin 23̊ 30´cos76̊ 30´ + sin 76̊ 30´ cos23̊ 30´
б) сos24̊ cos21̊ - sin 24̊ sin21̊
в) sin  cos
cos  –sin
–sin  cos
cos 
г) cos  cos
cos 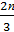 +sin
+sin  sin
sin 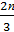
д) 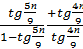
2. Вычислить, представив аргумент в виде суммы или разности:
а) sin15̊
б) cos75̊
в) tg 120̊
3. Вычислить:
а) sin(-  ) +3cos
) +3cos  +6sin
+6sin 
б) 2sin  +4sin
+4sin  +tg(-
+tg(-  )
)
в) 2sin 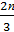 – ctg
– ctg 
г) 2cos  +tg
+tg 
4. Упростить выражение:
 -
- 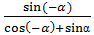
5. Вычислить:
а) cos α, если sinα= 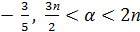
б) sinα и tg α, если cosα = - 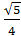 , п
, п 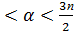
в) существует ли угол, для которого выполняется sinα= 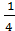 , cosα =
, cosα = 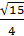
Вариант 3
1. Вычислить:
а) sin 105 ̊ 30´cos15 ̊ 30´ - sin 105̊ 30´ cos15̊ 30´
б) сos64̊ cos26 - sin 64̊ sin26̊
в) sin  cos
cos 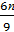 –sin
–sin  cos
cos 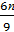
г) cos  cos
cos  - sin
- sin  sin
sin 
д) 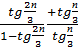
2. Вычислить, представив аргумент в виде суммы или разности:
а) sin75̊
б) cos75̊
в) tg 15̊
3. Вычислить:
а) sin(-  ) +3cos
) +3cos  +6sin
+6sin 
б) 2sin  +4sin
+4sin  +tg(-
+tg(-  )
)
в) 2sin 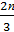 – ctg
– ctg 
г) 2cos  +tgп
+tgп
4. Упростить выражение:
 -
- 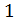
5. Вычислить:
а) cos α, если sinα= 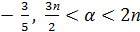
б) sinα и tg α, если cosα = - 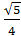 , п
, п 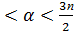
в) существует ли угол, для которого выполняется sinα= 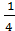 , cosα =
, cosα = 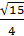
Контрольная работа №6
Вариант 1
1. Решите уравнение, сделав подстановку (I тип):
2 sin2 x – 5 sin x + 2 = 0
2. Решите уравнение, упростив левую часть:
__
2 sin x + Ö3 = 0
3. Решите уравнение, используя однородность (деление на cos2 x II тип)
sin2 x – 3sin x cos x + 2 cos 2 x = 0
4. Решите уравнение методом разложения на множители (III тип):
5 sin x + 3 sin 2x = 0
5. Решите систему уравнений
x + y = p2
__
Ö3 + cos 2x = cos 2y
Вариант 2
1. Решите уравнение, сделав подстановку (I тип):
2 cos 2 x + 5 cos x + 2 = 0
2. Решите уравнение, упростив левую часть:
__
Ö2 cos x - 1= 0
3. Решите уравнение, используя однородность (деление на cos2 x II тип)
3sin2 x + 4sin x cos x + cos 2 x = 0
4. Решите уравнение методом разложения на множители (III тип):
3 cos x – 2 sin 2x = 0
5. Решите систему уравнений
x + y = p2
__
Ö3 + cos 2x = cos 2y
Контрольная работа №7
Вариант № 1.
1) Площадь основания правильной 4- угольной призмы 36 см2 диагональ призмы наклонена к основанию под углом 300 . Найдите площадь диагонального сечения.
2) Найдите высоту прямого конуса
|
|
|
12 |


