 |
Математическая модель объекта регулирования
|
|
|
|
Исследование работы автоматической системы регулирования
Исходные данные для расчета АСР
. Кривая разгона объекта регулирования:
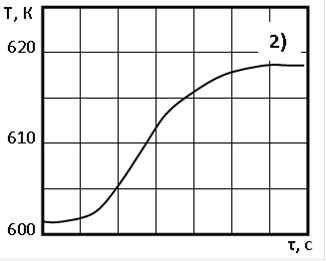
. Шкала времени:
. Возмущающее воздействие, D x = 5%.
. Максимальное возмущающее воздействие, D xmax = 12%.
. Показатели качества регулирования:
- тип переходного процесса - s = 20%
- D y 1 (t) = 28 К;
- D y ст = 6 К;
- t р = 430 с.
Идентификация объекта регулирования
математический регулятор переходный
Под идентификацией объекта управления понимается подбор модели, которая адекватно отражает динамические свойства конкретного объекта. Обычно используется методика структурно-параметрической идентификации, основанная на подборе типовой модели по экспериментальным данным, которые характеризуют реакцию объекта на ступенчатое или гармоническое воздействие. Выбирается структура модели, а затем определяются численные значения ее параметров. Решение задачи завершается проверкой адекватности найденной модели.
Определение параметров объекта регулирования
Кривая разгона объекта регулирования - это график процесса изменения выходной величины в результате воздействия на объект ступенчатого возмущения. Кривая разгона служит для определения динамических свойств объекта.
Для определения параметров, характеризующих динамические свойства объекта, необходимо построить касательную к кривой разгона в точке перегиба А (точка с максимальной скоростью изменения параметра). Интервал времени ОC от ввода возмущения до пересечения касательной с горизонталью начального значения параметра Y0 определит время запаздывания объекта τЗ.
Интервал времени от точки пересечения касательной с горизонталью начального значения параметра Y0 до точки ее пересечения с линией нового установившегося значения представляет постоянную времени объекта Т0 (отрезок C1 D1).
|
|
|
По графику кривой разгона определяются:
- время запаздывания τз = ОС1 = 62 с;
- постоянная времени объекта 
= С1Д1 = ОД1 - ОС1 =160-62 =98с
Коэффициент передачи объекта КОБ,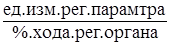 
, определяется по формуле
,
где Y1 - значение регулируемого параметра после завершения переходного процесса, ед. изм. рег. параметра;
Y0 - значение регулируемого параметра до нанесения возмущения, ед. изм. рег. параметра;
DX - возмущающее воздействие, нанесенное регулирующим органом, % хода регулирующего органа.
Таким образом коэффициент передачи объекта для данной кривой разгона:
КОБ = 
= 3,4 
Коэффициент самовыравнивания КС определяется по кривой разгона как отношение изменения входной величины (возмущения) к изменению выходной (регулируемого параметра). Эти изменения выражают в относительном виде: входную величину как отношение хода исполнительного механизма при вводе возмущения к его полному ходу DХ / 100, а выходную - как отношение изменения регулируемого параметра к его заданному значению ∆Y∞ / Y0:
;
Коэффициент самовыравнивания для данной кривой разгона:
;
КС =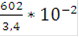 
= 1,77.
Математическая модель объекта регулирования
В результате проведенного при выполнении п. 2.1 исследования установлено, что для заданного в варианте объекта присущи свойства самовыравнивания, запаздывания и инерционности. На основании чего структуру объекта можно представить состоящей из двух типовых звеньев: звена чистого запаздывания и апериодического (инерционного) звена первого порядка (т.е. выполнена структурная идентификация объекта регулирования).
Математическая модель объекта при такой структуре может быть представлена кусочной функцией, имеющей вид
|
|
|
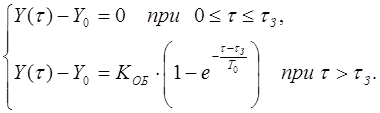
где e - основание натуральных логарифмов.
Заданная переходная функция при этом заменяется экспоненциальной зависимостью, график которой смещен относительно начала координат на величину времени запаздывания tЗ.
Заменяя и подставляя значения параметров tЗ, Т0, КОБ, получим первую математическую модель заданного объекта регулирования:
Модель объекта можно представить также с использованием преобразования Лапласа в виде его передаточной функции W(p)ОБ, которая равна произведению передаточных функций двух выше названных типовых динамических звеньев
,
где р - оператор Лапласа;
е - основание натуральных логарифмов.
Заменяя и подставляя значения параметров tЗ, Т0, КОБ, получим вторую математическую модель заданного объекта регулирования:
.
Формальная замена оператора Лапласа р в последнем выражении на комплексную переменную jω позволяет получить еще один вид математической модели объекта в виде его амплитудно-фазовой частотной характеристики W(jω)ОБ
,
где j - мнимая единица (
);
ω - угловая частота колебаний, рад/с.
Таким образом получаем третью математическую модель заданного объекта регулирования:
.
|
|
|
