 |
Анализ оптимального решения на чувствительность в Excel
|
|
|
|
Решение задачи ЛП средствами EXCEL
Описание ситуации.
Требуется определить план выпуска 4 видов продукции. На изготовление расходуются трудовые ресурсы, сырье и финансы. Границы выпуска каждого вида продукции, а так же наличие и нормы расхода ресурсов, прибыль на единицу продукции приведены в таблице:
| Ресурсы | Продукт 1 | Продукт 2 | Продукт 3 | Продукт 4 | Наличие |
| Труд | |||||
| Сырье | |||||
| Финансы | 10р. | 8р. | 10р. | 15р. | 180р. |
| нижн. гр. | |||||
| верхн. гр. | - | ||||
| Прибыль | 800р. | 700р. | 1 200р. | 1 500р. |
Необходимо создать производственный план, обеспечивающий наибольшую прибыль.
Выполнить анализ полученных результатов и ответить на следующие вопросы:
1. Выгодно ли включать в производственный план новые продукты со следующими характеристиками:
| Ресурсы | Продукт 1 | Продукт 2 |
| Труд | ||
| Сырье | ||
| Финансы | 8р. | 5р. |
| Прибыль | 1000р. | 1200р. |
2. Вырастет ли прибыль, если привлечь:
· дополнительные финансовые средства в размере 20 рублей?
· дополнительное сырье по цене 100 рублей?
3. На сколько увеличится прибыль, если привлечь дополнительно сырья:
· 5 единиц?
· 10 единиц?
4. Изменится ли выпуск:
· Продукта 1, если прибыль на него вырастет до 1100 рублей?
· Продукта 4, если прибыль на него снизится до 600 рублей?
Обозначив количество выпускаемой продукции через x1, x2, x3, x4, а целевую функцию (валовую прибыль) – через F, построим математическую модель задачи: F = 800x1 + 700x2 + 1200x3 + 1500x4 max,
Три неравенства – ограничения на ресурсы:
2 x1 + 1 x2 + 2 x3 + 2 x4 ≤ 36,
8 x1 + 5 x2 + 6 x3 + 5 x4 ≤ 85,
10 x1 + 8 x2 + 10 x3 + 15 x4 ≤ 180;
|
|
|
четыре неравенства – ограничения на выпуск:
1 ≤ x1 ≤ 6,
1 ≤ x2,
2 ≤ x3 ≤ 4,
2 ≤ x4 ≤ 5.
Создание в Excel модели для решения задачи и ввод в нее условий задачи
Для решения задачи средствами Excel удобно подготовить на листе Excel модель следующего вида:
Для создания модели используются формулы расчета общей прибыли и определения количества ресурсов, необходимых на выпуск продукции. Эти формулы удобно задавать при помощи функции СУММПРОИЗВ.
Для задания ограничений на выпуск удобно сделать ссылки на ячейки, в которых будет выводиться количество выпускаемой продукции.
Решение задачи в Excel
Для решения задачи используется команда Сервис/Поиск решения.
Если такой команды в меню нет, то необходимо выполнить команду Сервис/Надстройки и установить Поиск решения.
После выполнения команды появится окно:
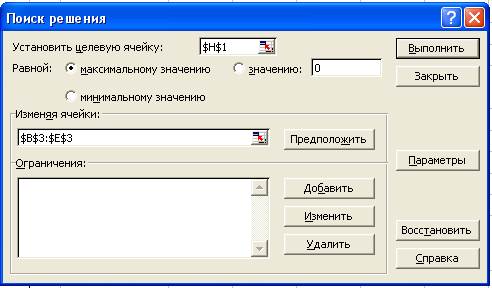
Задать ячейку с целевой функцией, изменяемые ячейки, ограничения.
Добавление ограничений:
Задать параметры поиска решения:
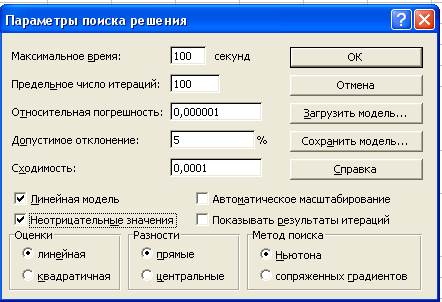
Параметр "Максимальное время" служит для назначения времени (в секундах), выделяемого на решение задачи. В поле можно ввести время, не превышающее 32 767 секунд (более 9 часов).
Параметр "Предельное число итераций" служит для управления временем решения задачи путем ограничения числа промежуточных вычислений. В поле можно ввести количество итераций, не превышающее 32 767.
Параметр "Относительная погрешность" служит для задания точности, с которой определяется соответствие ячейки целевому значению или приближение к указанным границам. Поле должно содержать число из интервала от 0 до 1. Чем меньше количество десятичных знаков во введенном числе, тем ниже точность. Высокая точность увеличит время, которое требуется для того, чтобы сошелся процесс оптимизации.
Параметр "Допустимое отклонение" служит для задания допуска на отклонение от оптимального решения в целочисленных задачах. При указании большего допуска поиск решения заканчивается быстрее.
|
|
|
Параметр "Сходимость" применяется только при решении нелинейных задач.
Установка флажка "Линейная модель" обеспечивает ускорение поиска решения линейной задачи за счет применение симплекс-метода. При этом в отчете по устойчивости, который можно получить после решения задачи, будет выводиться более полная информация.
Параметр "Неотрицательные значения" позволяет установить нулевую нижнюю границу для тех изменяемых ячеек, для которых она не была указана в ограничениях.
Параметр "Автоматическое масштабирование" служит для включения автоматической нормализации входных и выходных значений, качественно различающихся по величине — например, максимизация прибыли в процентах по отношению к вложениям, исчисляемым в миллионах рублей.
Параметр "Показывать результаты итераций" служит для приостановки поиска решения для просмотра результатов отдельных итераций.
Параметр "Оценка" служит для указания метода экстраполяции — линейная или квадратичная — используемого для получения исходных оценок значений переменных в каждом одномерном поиске.
Параметр "Производные" служит для указания метода численного дифференцирования — прямые или центральные производные — который используется для вычисления частных производных целевых и ограничивающих функций.
Параметр "Метод" служит для выбора алгоритма оптимизации — метод Ньютона или сопряженных градиентов — для указания направление поиска.
Для нахождения решения нажать кнопку «Выполнить» в окне Поиска решения.
В появившемся окне «Результаты поиска решения» отображается информация о том, найдено или нет решение, в этом окне можно выбрать тип отчета.
Иногда сообщения о том, найдено или нет оптимальное решение свидетельствуют не о характере оптимального решения задачи, а о том, что при вводе условий задачи в Excel были допущены ошибки, не позволяющие Excel найти оптимальное решение, которое в действительности существует.
В окне "Результаты поиска решения" представлены названия трех типов отчетов: "Результаты", "Устойчивость", "Пределы". Для выбора нужных отчетов необходимо выделить их названия. Отчет будет представлен на отдельном листе рабочей книги Excel.
|
|
|
Описание отчетов:
Результаты. Используется для создания отчета, состоящего из целевой ячейки и списка влияющих ячеек модели (ячеек с исходными данными), их исходных и конечных значений, а также формул ограничений и дополнительных сведений о наложенных ограничениях.
Устойчивость. Используется для создания отчета, содержащего сведения о чувствительности решения к малым изменениям в формуле (поле Установить целевую ячейку, диалоговое окно Поиск решения) или в формулах ограничений. В случае нелинейных моделей отчет содержит данные для градиентов и множителей Лагранжа. В отчет по нелинейным моделям включаются ограниченные затраты, фиктивные цены, объективный коэффициент (с некоторым допуском), а также диапазоны ограничений справа.
Пределы. Используется для создания отчета, состоящего из целевой ячейки и списка влияющих ячеек модели, их значений, а также нижних и верхних границ. Нижним пределом является наименьшее значение, которое может содержать влияющая ячейка, в то время как значения остальных влияющих ячеек фиксированы и удовлетворяют наложенным ограничениям. Соответственно, верхним пределом называется наибольшее значение (используется реже).
Отчеты по устойчивости и по пределам нельзя получить, если на изменяемые переменные наложены ограничения целочисленности. Для получения более полной информации в отчете по устойчивости нужно в окне задания параметров установить флажок "Линейная модель ".
Для получения же ответа (значений переменных, ЦФ и левых частей ограничений) прямо в экранной форме можно сразу нажать кнопку "OK". После этого в экранной форме появляется оптимальное решение задачи.
Анализ оптимального решения на чувствительность в Excel
Для проведения анализа на полученного решения чувствительность (т.е. для ответа на поставленные вопросы) необходимо после запуска в Excel задачи на решениев окне "Результаты поиска решения" выделить с помощью мыши два типа отчетов: "Результаты" и "Устойчивость".
|
|
|
Отчет по результатам
Отчет по результатам состоит из трех таблиц:
· таблица 1 содержит информацию о ЦФ;
· таблица 2 содержит информацию о значениях переменных, полученных в результате решения задачи;
· таблица 3 показывает результаты оптимального решения для ограничений и для граничных условий.
Если ресурс используется полностью (то есть ресурс дефицитный), то в графе "Статус" соответствующее ограничение указывается как "связанное"; при неполном использовании ресурса (то есть ресурс недефицитный) в этой графе указывается "не связан". В графе "Значение" приведены величины использованного ресурса.
Для граничных условий (ограничения на выпуск) в графе "Разница" показана разность между значением переменной в найденном оптимальном решении и заданным для нее граничным условием.
Таблица 3 отчета по результатам дает информацию для анализа возможного изменения запасов недефицитных ресурсов при сохранении полученного оптимального значения ЦФ. Если на ресурс наложено ограничение типа 
, то в графе "Разница" дается количество ресурса, которое не используется при реализации оптимального решения.
Так, анализ первой строки показывает, что трудового ресурса используется 25,6 ч/час. Неизрасходованным остается 10,4 ч/час из общего фонда времени, отведенного на выпуск продукции. Из этого следует, что запас недефицитного ресурса Труд можно уменьшить на 10,4 ч/час и это никак не повлияет на оптимальное решение.
Анализ строки 8 показывает, что общее количество выпускаемой Продукта 1 составляет 1 т, что меньше предполагаемой емкости рынка на 5 т. То есть уменьшение спроса до 1 т никак не скажется на оптимальных объемах выпуска этой продукции.
Отчет по устойчивости
Отчет по устойчивости состоит из двух таблиц.
Таблица 1 содержит информацию, относящуюся к переменным:
· Результ. значение показывает результат решения задачи.
· Нормированная стоимость показывает, на сколько изменится значение ЦФ в случае принудительного включения единицы этой продукции в оптимальное решение. Если нормированная стоимость какого-либо процесса положительна, то это значит, что стоимость потребленных ресурсов (в теневых ценах) больше возможной прибыли и значение соответствующей переменной в оптимальном решении равно 0. Если значения переменных > 0 в оптимальном решении (т.е. выпуск соответствующей продукции включен в оптимальный план), то нормированные стоимости у них равны 0. У нас в примере все 0, т.е. вся продукция включена в план выпуска.
|
|
|
· Коэффициенты ЦФ отображают исходные данные.
· Допустимое увеличение и уменьшение показывают предельные значения приращения целевых коэффициентов ∆Сj, при которых сохраняется первоначальное оптимальное решение. Например, допустимое увеличение цены на Продукт 1 равно 320 руб., а допустимое уменьшение – практически не ограничено. Это означает, что если цена на Продукт 1 возрастет более чем на 320 руб., например станет равной 1130 руб., то оптимальное решение изменится. А если их цена будет снижаться вплоть до нуля, то оптимальное решение останется прежним.
Примечание. При выходе за указанные в отчете по устойчивости пределы изменения цен оптимальное решение может меняться как по номенклатуре выпускаемой продукции, так и по объемам выпуска (без изменения номенклатуры).
Таблица 2 содержит информацию, относящуюся к ограничениям.
· Результ. значение показывает величина использованных ресурсов.
· Теневая цена показывает ценность дополнительной единицы соответствующего ресурса. Теневая цена рассчитывается только для дефицитных ресурсов, для недефицитных равна 0. Она показывает, на сколько возрастет значение целевой функции при увеличении запаса соответствующего ресурса на 1.
· Ограничение правая часть показывает исходные данные из правых частей ограничений.
· Допустимое увеличение и уменьшение показывают предельные значения приращения ресурсов ∆Bi. В графе " Допустимое Уменьшение " показывается, на сколько можно уменьшить (устранить излишек) или увеличить (повысить минимально необходимое требование) ресурс, сохранив при этом оптимальное решение. Рассмотрим анализ дефицитных ресурсов, так как анализ недефицитных ресурсов был дан выше. Анализируя отчет по результатам, мы установили, что существуют причины (ограничения), не позволяющие выпускать большее, чем в оптимальном решении, количество продукции и получать более высокую прибыль. В рассматриваемой задаче таким ограничением является дефицитный ресурс “Сырье”. Поскольку знак ограничений этих запасов имеет вид <=, то возникает вопрос, на сколько максимально можно увеличить запас ресурса, чтобы обеспечить увеличение выпуска продукции. Ответ на этот вопрос показан в графе "Допустимое Увеличение". Емкость сушилки имеет смысл увеличить самое большее на 6,375 единиц. Это приведет к увеличению прибыли по сравнению с текущим оптимальным решением. Дальнейшее увеличение запасов сырья сверх указанных пределов не будет больше улучшать решение, т.к. уже другие ресурсы станут связывающими.
Теперь ответим на поставленные вопросы:
1) Выгодно ли включать в производственный план новые продукты со следующими характеристиками:
| Ресурсы | Продукт 1 | Продукт 2 |
| Труд | ||
| Сырье | ||
| Финансы | 8р. | 5р. |
| Прибыль | 1000р. | 1200р. |
2 * 0 + 4 * 140 + 8 * 0 = 560 < 1000 выгодно
1 * 0 + 12 * 140 + 5 * 0 = 1680 > 1200 не выгодно
2) Вырастет ли прибыль, если привлечь:
· дополнительные финансовые средства в размере 20 рублей?
Нет, т.к. финансовые средства и так не полностью используются.
· дополнительное сырье по цене 100 рублей?
Да, т.к. дополнительно привлечь единицу сырья. То прибыль увеличится на 140 руб.
3) На сколько увеличится прибыль, если привлечь дополнительно сырья:
· 5 единиц? (5 * 140 – 5 * 100)
· 10 единиц? (6,375 * 140 – 10 * 100 = 892,5 - 1000)
4) Изменится ли выпуск:
· Продукта 1, если прибыль на него вырастет до 1100 рублей? (нет, не изменится, т.к. предельное увеличение 800 + 320)
· Продукта 4, если прибыль на него снизится до 600 рублей? (да, изменится, т.к. допустимое уменьшение 1500 – 800 = 700)
|
|
|
