 |
Решето только по нечётным числам
|
|
|
|
Решето Эратосфена
Решето Эратосфена — это алгоритм, позволяющий найти все простые числа в отрезке 
за 
операций.
Идея проста — запишем ряд чисел 
, и будем вычеркивать сначала все числа, делящиеся на 
, кроме самого числа , затем деляющиеся на 
, кроме самого числа , затем на 
, затем на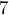 
, 
, и все остальные простые до 
.
Реализация
Сразу приведём реализацию алгоритма:
int n;vector<char> prime (n+1, true);prime[0] = prime[1] = false;for (int i=2; i<=n; ++i) if (prime[i]) if (i * 1ll * i <= n) for (int j=i*i; j<=n; j+=i) prime[j] = false;Этот код сначала помечает все числа, кроме нуля и единицы, как простые, а затем начинает процесс отсеивания составных чисел. Для этого мы перебираем в цикле все числа от до , и, если текущее число 
простое, то помечаем все числа, кратные ему, как составные.
При этом мы начинаем идти от 
, поскольку все меньшие числа, кратные , обязательно имеют простой делитель меньше , а значит, все они уже были отсеяны раньше. (Но поскольку легко может переполнить тип 
, в коде перед вторым вложенным циклом делается дополнительная проверка с использованием типа 
.)
При такой реализации алгоритм потребляет 
памяти (что очевидно) и выполняет действий (это доказывается в следующем разделе).
Асимптотика
Докажем, что асимптотика алгоритма равна .
Итак, для каждого простого 
будет выполняться внутренний цикл, который совершит 
действий. Следовательно, нам нужно оценить следующую величину:
Вспомним здесь два известных факта: что число простых, меньше либо равных , приблизительно равно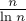 
, и что 
-ое простое число приблизительно равно 
(это следует из первого утверждения). Тогда сумму можно записать таким образом:
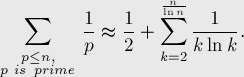
Здесь мы выделили первое простое из суммы, поскольку при 
согласно приближению получится 
, что приведёт к делению на нуль.
|
|
|
Теперь оценим такую сумму с помощью интеграла от той же функции по от до 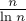(мы можем производить такое приближение, поскольку, фактически, сумма относится к интегралу как его приближение по формуле прямоугольников):
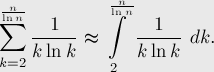
Первообразная для подынтегральной функции есть 
. Выполняя подстановку и убирая члены меньшего порядка, получаем:
Теперь, возвращаясь к первоначальной сумме, получаем её приближённую оценку:
что и требовалось доказать.
Более строгое доказательство (и дающее более точную оценку с точностью до константных множителей) можно найти в книге Hardy и Wright "An Introduction to the Theory of Numbers" (стр. 349).
Различные оптимизации решета Эратосфена
Самый большой недостаток алгоритма — то, что он "гуляет" по памяти, постоянно выходя за пределы кэш-памяти, из-за чего константа, скрытая в , сравнительно велика.
Кроме того, для достаточно больших узким местом становится объём потребляемой памяти.
Ниже рассмотрены методы, позволяющие как уменьшить число выполняемых операций, так и значительно сократить потребление памяти.
Просеивание простыми до корня
Самый очевидный момент — что для того, чтобы найти все простые до , достаточно выполнить просеивание только простыми, не превосходящими корня из .
Таким образом, изменится внешний цикл алгоритма (укажите, как именно)
На асимптотику такая оптимизация не влияет (действительно, повторив приведённое выше доказательство, мы получим оценку 
, что, по свойствам логарифма, асимптотически есть то же самое), хотя число операций заметно уменьшится.
Решето только по нечётным числам
Поскольку все чётные числа, кроме , — составные, то можно вообще не обрабатывать никак чётные числа, а оперировать только нечётными числами.
Во-первых, это позволит вдвое сократить объём требуемой памяти. Во-вторых, это уменьшит число делаемых алгоритмом операций примерно вдвое.
|
|
|
|
|
|
