 |
Электрическая цепь, содержащая ОП.
|
|
|
|
Электрические цепи с нелинейными преобразователями и оперативная коррекция режима энергосистемы
Хмельник С.И., к.т.н.
Институт "Энергосетьпроект", Москва
Рассматриваются электрические цепи с нелинейными преобразователями. Показывается, что в такимх цепях достигается оптимум некоторой выпуклой функции токов электрической цепи. Далее рассматривается задача оперативной коррекции режима энергосистемы и формулируется критерий качества оптимизации режима по активной мощности. Показывается, что этот критерий совпадает с вышеуказанной функцией с точностью до обозначений. Тем самым задача оперативной коррекции сводится к расчету определенной электрической цепи или к решению задачи выпуклого программирования. Указывается метод решения этой задачи
Простая электрическая цепь
Рассмотрим электрическую цепь с источниками тока, подключенными к узлам цепи, и источниками напряжения, включенным в ветви цепи. Такая электрическая цепь описывается следующей системой уравнений:
, (1)
, (2)
где
H - вектор токов, создаваемых источниками тока;
I - вектор токов в ветвях цепи;
E - вектор напряжений в ветвях цепи;
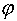- вектор узловых потенциалов;
N - матрица инциденций с элементами 1,0,-1;
R - диагональная матрица сопротивлений в ветвях цепи.
В этой системе уравнение (2) описывает первый закон Кирхгофа, уравнениe (1) - второй закон Кирхгофа.
Рассмотрим функцию
. (3)
Необходимые условия оптимума этой функции при ограничениях вида (2) имеют вид уравнения (1), где 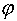является вектором неопределенных множителей Лагранжа для условия (2), которые появляются, когда оптимизируемая функция дополняется слагаемым 
. Далее имеем:
(4)
|
|
|
Отсюда следует, что функция (3), имеет глобальный минимум. Итак, минимизация функции (3) при ограничении в виде уранений первого закона Кирхгофа (2) приводит к уравнениям второго закона Кирхгофа (1). Следовательно, расчет электрической цепи постоянного тока эквивалентен поиску минимума функции (3) при ограничении (2). Другими словами электрическая цепь моделирует задачу квадратичного программирования.
Деннис в [1] показал, что все эти выводы справедливы и в том случае, когда электрическая цепь содержит диоды и так называемые трансформаторы постоянного тока, которые мы далее будем называть трансформаторами Денниса - ТД.
Диоды описываются неравенствами и равенством вида
(5)
(6)
. 
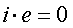(7)
Необходимые условия оптимума функции (3) при ограничениях вида (5) имеют вид (6, 7).
Трансформатор Денниса ТД содержит две ветви - первичную с током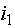 
и напряжением 
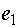и вторичную с током 
и напряжением.Он описываются уравнениями
(8)
(9)
где h - коэффициент трансформации. Из этих уравнений следует, что
(10)
т.е. мощности, отдаваемые первичной и вторичной ветвями ТД в электрическую цепь, в сумме равны нулю. Необходимые условия оптимума функции (3) при ограничениях вида (8) имеют вид (9).
Обратимые преобразователи
Обратимый преобразователь (ОП) предложен в [2] и представляет собой устройство, содержащее две ветви - первичную с током 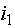и напряжением 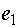и вторичную с током и напряжением 
. В нем (в отличие от ТД) токи ветвей зависят от напряжений смежных ветвей следующим образом:
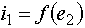(1)
(2)
где 
- дифференцируемая функция. Будем обозначать ОП так, как показано на фиг. 2.1.
В частности, при, где h - константа (коэффициент преобразования), этот преобразователь является линейным - (ЛОП). В нем токи ветвей зависят от напряжений смежных ветвей следующим образом:
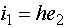(3)
(4)
Отсюда следует, что
(5)
т.е. мощности, отдаваемые первичной и вторичной ветвями ЛОП в электрическую цепь, в сумме равны нулю (также как и в ТД).
|
|
|
Пример 2.1.. Конструкция ЛОП представлена на фиг. 2.2. Он состоит из двух источников тока VC-1 и VC-2, управляемых напряжением: напряжение на одном из них является управляющим для другого
В общем случае ОП является нелинейным (НОП).
Пример 2.2. В [3] рассмотрен синусно-косинусный преобразователь СКП, в котором
(6)
(7)
Известно, что для энергетических расчетов можно принять
(8)
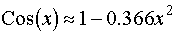(9)
В этом случае СКП может быть реализован на сумматорах и умножителях.
Электрическая цепь, содержащая ОП.
Уравнения электрической цепи, содержащей ОП, учитывают тот факт, что в некоторые ветви влючены первичные или вторичные ветви ОП, а некоторые из токов ветвей являются одновременно первичными или вторичными токами ОП [2]. Эти уравнения имеют следующий вид:
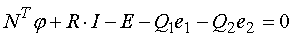(1)
(2)
(3)
(4)
где
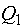- диагональная матрица, в которой "1" находятся в элементах, соответствующих ветвям, состоящим из первичных цепей ОП,
- диагональная матрица, в которой "1" находятся в элементах, соответствующих ветвям, состоящим из вторичных цепей ОП.
Рассмотрим функцию
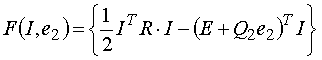(5)
Необходимые условия оптимума этой функции при ограничениях вида (2) и (3) имеют вид уравнений (1) и (4), где
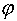является вектором неопределенных множителей Лагранжа для условия (2), когда оптимизируемая функция дополняется слагаемым,
является вектором неопределенных множителей Лагранжа для условия (3), когда оптимизируемая функция дополняется слагаемым 
.
Таким образом, расчет данной электрической цепи эквивалентен поиску безусловного оптимума функции
(6)
Далее имеем:
, 
, 
,
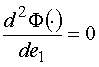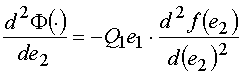
Отсюда следует, что функция (11) имеет глобальный минимум при
. 
(7)
Это имеет место, например, при и, в частности, для ЛОП. Синусно-косинусный преобразователь СКП, рассмотренный в примере 2.2, удовлетворяет соотношению (7) при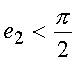 
.
Таким образом, при соблюдении условия (7) в электрической цепи достигается глобальный минимум некоторой выпуклой функции (6) токов I, потенциалов и напряжений E электрической цепи. Все эти выводы справедливы и в том случае, когда она содержит трансформаторами Денниса и диоды. Последнее означает, что математическая модель (1-4) электрической цепи с ОП может быть дополнена неравенствами вида (1.5-1.7):
|
|
|
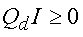(8)
(9)
(10)
где
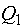- диагональная матрица, в которой "1" находятся в элементах, соответствующих ветвям, содержащим диоды,
- напряжения на диодах
При этом в электрической цепи, содержащей ОП и диоды, достигается минимум функции (6) при ограничении (8). Этот минимум является глобальным при выполнении условия (7)
|
|
|
12 |
