 |
Пространство товаров и система предпочтений
|
|
|
|
Одним из основных элементов — участников экономики — является домашнее хозяйство, определяемое как некоторая группа индивидуумов, выступающая как единое целое, распределяющая свой доход на покупку и потребление товаров и услуг. В общем, участник экономики, рассматриваемый с этой точки зрения, называется потребителем. Проблема рационального поведения потребителя заключается в решении вопроса о том, какие количества товаров или услуг он хочет и может приобрести при заданных ценах и его доходе.
Специально отметим, что существуют разные точки зрения на роль индивидов-потребителей. В неоклассической экономической теории эта роль является основной, определяющей. Вся остальная экономика вырастает из желаний и потребностей такого индивида.
Выше была сформулирована аксиома потребителя, полностью описывающая его поведение в вопросах потребления. Эта аксиома чрезвычайно упрощает анализ поведения потребителя.
Выбор потребителем некоторого набора товаров во многом зависит от его вкусов, желаний.
Запись y ≤ x означает, что потребитель предпочитает набор x набору y или не делает между ними различий, запись x ~ y – оба набора обладают одинаковой степенью предпочтения.
Потребуем выполнение следующих аксиом:
1) x ≥ x, для любого x (рефлексивность);
2) если x ≥ y, y ≥ z, то х ≥ z (транзитивность);
3) для любой пары x, y либо x ≥ y, либо y ≥ x, либо и то и другое.
Кроме аксиом 1 – 3 на отношение предпочтения накладывают ряд других ограничений, главными из которых являются непрерывность и ненасыщаемость.
Отношение предпочтения f называется непрерывным на множестве Х, если множество { (x,y) | x ≥ y } является открытым подмножеством декартова произведения X × X, т.е. если набор товаров x0 строго предпочтительнее набора y0, то при малом изменении каждого из этих наборов отношение строгого предпочтения сохраняется.
|
|
|
Точкой насыщения называется наиболее предпочтительный набор х ∈ Х, т.е. такой, что x ≥ y для всех х ∈ Х. Если Х не содержит точки насыщения, то говорят, что имеет место ненасыщаемости, то х > у (ненасыщаемость: больший набор всегда предпочтительнее меньшего).
На непрерывном множестве потребительских наборов можно задать числовую функцию u(x).
Функция u(x), определенная на множестве Х, называется функцией полезности, соответствующей отношению предпочтения f, если u(х) ≥ u(у) тогда и только тогда, когда x f y.
Для каждого потребителя такое представление многовариантно.
Математики называют отношение рефлексивным, если X < X для всякого X; симметричным, если X < Y влечет, что и Y < X; транзитивным, если X < Y и Y < Z влечет X < Z; совершенным (или полным), если для любых двух наборов X, Y либо X <Y, либо Y <Х.
Аксиома.
1) Отношение слабого предпочтения рефлексивно, транзитивно и совершенно;
2) Отношение равноценности рефлексивно, симметрично и транзитивно;
3) Отношение предпочтения транзитивно;
4) Для любого X ∈ С множество предпочтительности РX= {Y:X < Y) выпукло;
5) Каждый товар желателен для индивида: если X ≤ Y, то и X ≤ Y, а если к тому же Х ≠ Y (т.е. хi <yi для некоторого i), то Х< Y.
Подчеркнем, что это именно аксиома, выражающая фундаментальные свойства системы предпочтений индивида, вообще говоря, живого человека. Что касается рефлексивности и совершенности, то они представляются вполне понятными. Ведь рефлексивность означает, что любой набор товаров равноценен сам себе. А совершенность означает, что индивид в состоянии сравнить по привлекательности любые два набора товаров. Пятое свойство также понятно и в разъяснениях не нуждается.
|
|
|
Какой смысл в четвертом свойстве системы предпочтений? Выпуклость означает, что лучше иметь комбинацию товаров, пусть в меньших количествах, чем просто только какой-то один из этих товаров (лучше иметь немножко соли, сахара, кофе, хлеба, чем одну только соль, один сахар, кофе, хлеб, хотя бы и в большем количестве).
Свойство транзитивности, которым обладают отношения предпочтения и слабого предпочтения, не совсем очевидно, не очень наглядно и не сразу осознается потребителем, но если ему объяснить, что получится, если его система предпочтений не транзитивна, то он согласится, что свойство транзитивности должно быть, и произведет необходимую переоценку привлекательности для него тех или иных наборов товаров.
Потребительская корзина
Положение каждого потребителя с точки зрения наличия у него товаров, мы можем выразить с помощью потребительской корзины. В каждый данный момент времени потребителю доступно конечное число товаров, причем потребление некоторых из них должно быть не на нулевом уровне.
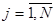– индекс товаров.
– индекс потребителя.
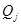– количество товаров вида j в системе (запас блага j в системе).
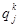– количество товара вида j, находящегося в распоряжении потребителя под номером k.
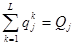– условие частной собственности (нет ничейных товаров).
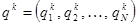– векторная величина; набор потребительских товаров у потребителя k.Некоторые значения могут быть равны 0 (нет товаров).
N=3
Получаем аналог N-мерного пространства, его положительную часть.
Любой точке этого пространства соответствует некий товарный набор. Все возможные товарные наборы, взятые вместе, образуют это пространство – пространство благ. Наша задача: для отдельно взятого потребителя научиться определять полезность каждого набора благ. В идеале, хорошо было бы иметь некоторую функцию, где вместо аргументов было бы количество благ. Подставляя в нее реальные значения, мы получили бы индекс полезности, с помощью которого могли бы сравнить любые наборы благ. Для большинства утверждений мы можем рассматривать товарное пространство на плоскости.
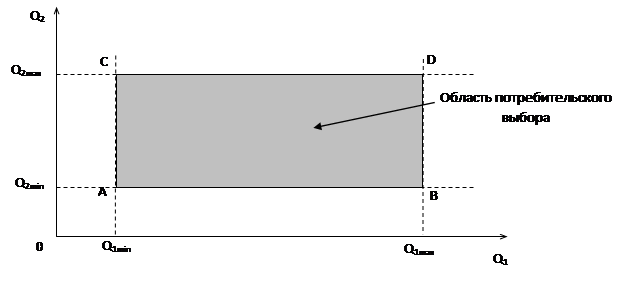
Q1min, Q2min – минимально необходимый набор благ.
B≥A; D≥B; D≥A; C≥A; D≥C; B? С – основная проблема.
|
|
|
Заключение
Понятие пространства товара является важнейшим в курсе математической экономики и, как мы указали, означает множество наборов товаров. Набор товаров можно трактовать, как корзину, в которой лежат эти товары в соответствующем количестве. Неотделимо от этого понятия следует также понятие цены, означающей себестоимость товара + набавки. Цена устанавливается на каждый товар индивидуально и определяет спрос и предложение на товар.
Из этих основополагающих понятий исходят и другие важные понятия математической экономики, такие как бюджетное множество, система предпочтений, функция полезности и т.д…, которые более подробно будут рассмотрены в других работах.
Список использованной литературы
1. В. И. Малыхин «Математика в экономике». Издательство: Инфра-М 2000
2. «Математика в экономике. Основы экономического анализа.». УСЭИ, Челябинск 2001. Составители: Забейворота В.И., Иванова В.Н., Завьялов В.Г.
3. Колемаев В.А. «Математическая экономика». Издательство: Юнити, 1998.
4. Ланкастер К «Математическая экономика». М., 1979.
5. Лифшиц А.Я. «Введение в рыночную экономику», M., 1991
6. «Введение в математический анализ.Учебное пособие по математике для студентов всех специальностей заочной формы обучения», ГТУ 2007.
7. Н. Н. Данилов «Курс математической экономики». Издательство: Высшая школа, 2006 г.
8. ru.wikipedia.org – Википедия свободная энциклопедия
9. http://mylearn.ru/kurs/29 - Математически модели в экономике
10. http://www.mathematica.ru
[1] ГОСТ Р 51303-99: «Товар — любая вещь, не ограниченная в обороте, свободно отчуждаемая и переходящая от одного лица к другому по договору купли-продажи.»
|
|
|
12 |
