III. Логарифмические уравнения

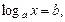
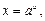
Основные свойства логарифмов.

1.

2.

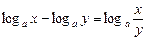
3.

4.

5.

6.

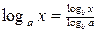
7.

II. ЛОГАРИФМИЧЕСКАЯ ФУНКЦИЯ

(§10, п.38)

Функция, заданная формулой , называется логарифмической функцией с основанием а.

Свойства логарифмической функции.

1. Область определения – множество

III. ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ

(§10,п.39)

Уравнение, содержащее переменную под знаком логарифма, называется логарифмическим.

Простейшим примером логарифмического уравнения служит уравнение

, где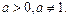

Решение данного уравнения опирается на определение логарифма, т.е.

, причем

Решение логарифмического уравнения вида

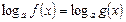
основано на том, что такое уравнение равносильно уравнению

,

при дополнительных условиях

Переход от уравнения

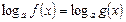
к уравнению

иногда приводит к появлению посторонних корней. Такие корни можно выявить либо при помощи подстановки найденных корней в исходное логарифмическое уравнение, либо с помощью нахождения области определения исходного уравнения (эта область задается системой неравенств ).

При решении логарифмических уравнений часто бывает полезен метод введения новой переменной.

При решении уравнений, содержащих переменную и в основании, и в показателе степени, используется метод логарифмирования. Если при этом в показателе степени содержится логарифм, то обе части уравнения надо прологарифмировать по основанию этого логарифма.

Пример 1. Решить уравнение: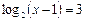

Решение:

Найдем область допустимых значений данного уравнения, решив неравенство

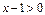, откуда .

Согласно определению логарифма, имеем:

или

Найденное значение удовлетворяет области допустимых значений (т.е. ), значит - корень уравнения.

Ответ:

Пример 2. Решить уравнение:

Решение:

Найдем область допустимых значений данного уравнения, решив систему неравенств:

, откуда или

решением этой системы является интервал

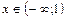
Перенесем логарифм из правой части уравнения в левую:

Применяя первое свойство логарифма, получим:

.

Используя определение логарифма (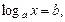 ), имеем:

или

Раскрывая скобки и приводя подобные члены, получим квадратное уравнение

,

,

решая которое, получим: .

Сравнивая полученные корни с областью допустимых значений, делаем вывод о том, что – посторонний корень, таким образом, исходное уравнение имеет единственное решение .

Ответ: .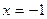

Пример 3. Решить уравнение:

Решение:

Областью допустимых значений данного уравнения является решение системы неравенств:

, откуда .

Применяя ко второму слагаемому исходного уравнения третье свойство логарифма, получим:

Введем новую переменную, пусть , тогда исходное уравнение примет вид:

,

решая которое, имеем: .

Возвращаясь к переменной х, получим:

, откуда .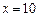

Сравнивая полученный результат с областью допустимых значений, можно сделать вывод о том, что 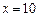- корень исходного уравнения.

Ответ: .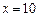

Пример 4. Решить уравнение:

Решение:

Данное уравнение имеет разные основания логарифмов, применяя ко второму слагаемому данного уравнения формулу перехода к новому основанию (см. шестое свойство), имеем:

Так как , то получаем:

Применим к левой части полученного уравнения второе свойство логарифма, а к правой части уравнения – пятое свойство:

, откуда (*)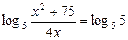

Так как в левой и в правой частях полученного уравнения содержится по одному логарифму с одинаковыми основаниями, то должны равняться и подлогарифмические выражения, то есть

или .

Решая полученное квадратное уравнение , имеем

.

Проверим полученные результаты, подставляя найденные значения х в выражение (*).

1.

; ; .

2.

; ; .

Проверкой установлено, что оба значения х являются решениями исходного уравнения.

Ответ: .