 |
Подписано в печать Формат 60х84/16. Бумага для множ. аппаратов
|
|
|
|
Задания и методические указания
Для выполнения контрольной работы
по дисциплине «статистика»
(ГОС–2000)
Для студентов всех форм обучения специальности
080503.65 Антикризисное управление (351000)
Екатеринбург 2009
Задания и методические указания для выполнения контрольной работы по дисциплине «статистика» (ГОС–2000). Екатеринбург: ГОУ ВПО «Российский государственный профессионально-педагогический университет», 2009. 54 с.
Настоящие контрольные задания и методические указания для выполнения контрольной работы по дисциплине «Статистика» составлены в соответствии с Государственным образовательным стандартом специальности 080503.65 Антикризисное управление (351000)
Составители: канд.физ.-мат.наук, доцент А.А. Меленцов,
канд.физ.-мат.наук, доцент А.С. Просвиров,
канд.физ.-мат.наук, доцент В.А. Реймер,
канд.физ.-мат.наук, доцент Л.С. Чебыкин
канд.физ.-мат.наук, доцент А.В.Шитиков
Одобрены на заседании кафедры высшей математики. Протокол от 26.02.2009, № 6.
Заведующий кафедрой ВМ Е.А. Перминов
Рекомендованы к печати методической комиссией Машиностроительного института РГППУ. Протокол от 16 марта 2009 г. № 7.
Председатель методической комиссии
МаИ РГППУ А.В.Песков
© ГОУ ВПО «Российский государственный профессионально-педагогический
университет», 2009
Указания к выполнению контрольной работы
Цель контрольной работы – закрепление и проверка знаний, полученных студентами заочной формы обучения в процессе самостоятельного изучения учебного материала, а так же выявление их умения применять на практике методы решения задач статистики.
Каждый студент заочной формы обучения должен решить все задачи своего варианта.
|
|
|
При выполнении контрольной работы необходимо руководствоваться следующими требованиями:
1. Вариант контрольной работы выбирать по последней цифре номера зачетной книжки (или по последней цифре порядкового номера Ф.И.О. студента в списке журнала группы, если он взят за основу при определении варианта); цифра "0" означает вариант 10.
2. В начале работы должен быть указан номер варианта задания;
3. Перед решением задачи должно быть приведено ее условие;
4. Решение задач следует сопровождать необходимыми формулами, развернутыми расчетами и краткими пояснениями;
5. В конце работы должна стоять подпись студента с указанием даты ее выполнения;
6. На лицевой стороне контрольной работы необходимо указать следующую информацию: ФИО студента, номер группы с указанием формы обучения, дисциплина и номер зачетной книжки (или, соответственно, порядковый номер Ф.И.О. студента в списке журнала группы).
Содержание контрольной работы
Задача 1.
Из генеральной совокупности 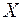 , распределенной по нормальному закону, извлечена выборка. Требуется:
, распределенной по нормальному закону, извлечена выборка. Требуется:
1. Составить вариационный, статистический и выборочный ряды распределения; найти размах выборки;
По полученному распределению выборки:
2. Построить полигон относительных частот;
3. Построить график эмпирической функции распределения;
4. Вычислить выборочную среднюю, выборочную дисперсию, выборочное исправленное среднее квадратическое отклонение, моду и медиану;
5. С надежностью  найти доверительные интервалы для оценки математического ожидания и среднего квадратического отклонения изучаемого признака генеральной совокупности.
найти доверительные интервалы для оценки математического ожидания и среднего квадратического отклонения изучаемого признака генеральной совокупности.
1.1. 
| 5,0 | 5,6 | 5,8 | 5,4 | 5,8 | 5,2 | 5,0 | 5,6 |
| 5,6 | 5,6 | 5,4 | 5,2 | 5,4 | 5,8 | 5,4 | 5,6 |
| 5,4 | 5,4 | 5,4 | 5,2 | 5,6 | 6,0 | 5,0 | 5,8 |
| 5,2 | 5,8 | 5,6 | 5,2 | 6,0 | 5,8 | 6,0 | 5,8 |
| 5,4 | 6,2 | 5,6 | 6,2 | 5,6 | 5,6 | 6,0 | 5,2 |
1.2. 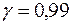
|
|
|
1.3. 
| 7,6 | 7,8 | 7,4 | 7,8 | 7,2 | 7,6 | ||
| 7,6 | 7,6 | 7,4 | 7,2 | 7,4 | 7,8 | 7,4 | 7,6 |
| 7,4 | 7,4 | 7,4 | 7,2 | 7,6 | 7,8 | ||
| 7,2 | 7,8 | 7,6 | 7,2 | 7,8 | 7,8 | ||
| 7,4 | 8,2 | 7,6 | 8,2 | 7,6 | 7,6 | 7,2 |
1.4. 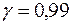
| 11,5 | 9,5 | 10,5 | 7,5 | 10,5 | 10,5 | 8,5 | 10,5 |
| 13,5 | 9,5 | 11,5 | 12,5 | 11,5 | 9,5 | 9,5 | 10,5 |
| 11,5 | 9,5 | 10,5 | 9,5 | 8,5 | 12,5 | 10,5 | 8,5 |
| 7,5 | 8,5 | 10,5 | 13,5 | 7,5 | 11,5 | 9,5 | 11,5 |
| 10,5 | 10,5 | 12,5 | 9,5 | 8,5 | 12,5 | 10,5 | 10,5 |
1.5. 
| 11,7 | 12,3 | 11,1 | 10,8 | 11,4 | 11,1 | 11,1 | 11,4 |
| 11,4 | 11,4 | 11,7 | 11,1 | 12,3 | 11,1 | 10,5 | |
| 10,8 | 10,5 | 10,8 | 11,1 | 11,7 | 11,7 | ||
| 11,4 | 11,1 | 11,4 | 11,4 | 11,4 | 10,8 | 11,4 | |
| 10,5 | 11,7 | 11,4 | 11,4 | 11,7 | 11,4 | 11,4 | 10,8 |
1.6. 
| 11,6 | 11,8 | 11,4 | 11,8 | 11,2 | 11,6 | ||
| 11,6 | 11,6 | 11,4 | 11,2 | 11,4 | 11,8 | 11,4 | 11,6 |
| 11,4 | 11,4 | 11,4 | 11,2 | 11,6 | 11,8 | ||
| 11,2 | 11,8 | 11,6 | 11,2 | 11,8 | 11,8 | ||
| 11,4 | 12,2 | 11,6 | 12,2 | 11,6 | 11,6 | 11,2 |
1.7. 
| 12,5 | 10,5 | 11,5 | 8,5 | 11,5 | 11,5 | 9,5 | 11,5 |
| 14,5 | 10,5 | 12,5 | 13,5 | 12,5 | 10,5 | 10,5 | 11,5 |
| 12,5 | 10,5 | 11,5 | 10,5 | 9,5 | 13,5 | 11,5 | 9,5 |
| 8,5 | 9,5 | 11,5 | 14,5 | 8,5 | 12,5 | 10,5 | 12,5 |
| 11,5 | 11,5 | 13,5 | 10,5 | 9,5 | 13,5 | 11,5 | 11,5 |
1.8. 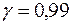
| 12,7 | 13,3 | 12,1 | 11,8 | 12,4 | 12,1 | 12,1 | 12,4 |
| 12,4 | 12,4 | 12,7 | 12,1 | 13,3 | 12,1 | 11,5 | |
| 11,8 | 11,5 | 11,8 | 12,1 | 12,7 | 12,7 | ||
| 12,4 | 12,1 | 12,4 | 12,4 | 12,4 | 11,8 | 12,4 | |
| 11,5 | 12,7 | 12,4 | 12,4 | 12,7 | 12,4 | 12,4 | 11,8 |
1.9. 
| 13,6 | 13,8 | 13,4 | 13,8 | 13,2 | 13,6 | ||
| 13,6 | 13,6 | 13,4 | 13,2 | 13,4 | 13,8 | 13,4 | 13,6 |
| 13,4 | 13,4 | 13,4 | 13,2 | 13,6 | 13,8 | ||
| 13,2 | 13,8 | 13,6 | 13,2 | 13,8 | 13,8 | ||
| 13,4 | 14,2 | 13,6 | 14,2 | 13,6 | 13,6 | 13,2 |
1.10. 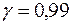
Задача 2.
Для выборки, извлеченной из генеральной совокупности и представленной интервальным рядом (в первой строке указаны интервалы значений  исследуемого количественного признака
исследуемого количественного признака 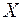 генеральной совокупности; во второй – частоты
генеральной совокупности; во второй – частоты 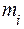 , т.е. количество элементов выборки, значения
, т.е. количество элементов выборки, значения  признака которых принадлежат указанному интервалу). Требуется:
признака которых принадлежат указанному интервалу). Требуется:
1) Построить полигон относительных накопленных частот (кумулятивную кривую);
2) Построить гистограмму частот и гистограмму относительных частот;
3) Найти выборочную среднюю, выборочную дисперсию, моду и медиану;
4) Проверить на уровне значимости 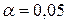 гипотезу о нормальном распределении признака
гипотезу о нормальном распределении признака 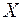 генеральной совокупности по критерию согласия Пирсона;
генеральной совокупности по критерию согласия Пирсона;
|
|
|
5) В случае согласованности с нормальным распределением найти с надежностью 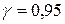 доверительные интервалы для оценки математического ожидания и среднего квадратического отклонения признака
доверительные интервалы для оценки математического ожидания и среднего квадратического отклонения признака 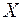 генеральной совокупности.
генеральной совокупности.
2.1.

| 6,5-7,0 | 7,0-7,5 | 7,5-8,0 | 8,0-8,5 | 8,5-9,0 | 9,0-9,5 | 9,5-10 |
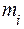
|
2.2.

| 0,3-0,4 | 0,4-0,5 | 0,5-0,6 | 0,6-0,7 | 0,7-0,8 | 0,8-0,9 | 0,9-1 |
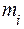
|
2.3.

| 3-4 | 4-5 | 5-6 | 6-7 | 7-8 | 8-9 | 9-10 |
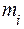
|
2.4.

| 0,6-0,95 | 0,95-1,30 | 1,30-1,65 | 1,65-2,00 | 2,00-2,35 | 2,35-2,70 | 2,70-3,05 |
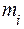
|
2.5.

| 0,6-0,9 | 0,9-1,2 | 1,2-1,5 | 1,5-1,8 | 1,8-2,1 | 2,1-2,4 | 2,4-2,7 |
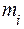
|
2.6.

| 6,5-7,0 | 7,0-7,5 | 7,5-8,0 | 8,0-8,5 | 8,5-9,0 | 9,0-9,5 | 9,5-10 |
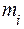
|
2.7.

| 0,3-0,4 | 0,4-0,5 | 0,5-0,6 | 0,6-0,7 | 0,7-0,8 | 0,8-0,9 | 0,9-1 |
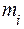
|
2.8.

| 3-4 | 4-5 | 5-6 | 6-7 | 7-8 | 8-9 | 9-10 |
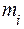
|
2.9.

| 0,6-0,95 | 0,95-1,30 | 1,30-1,65 | 1,65-2,00 | 2,00-2,35 | 2,35-2,70 | 2,70-3,05 |
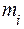
|
2.10.

| 0,6-0,9 | 0,9-1,2 | 1,2-1,5 | 1,5-1,8 | 1,8-2,1 | 2,1-2,4 | 2,4-2,7 |
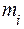
|
Замечание: При отыскании выборочной средней и выборочной дисперсии в задачах 2.5. и 2.6. для упрощения счета рекомендуется переходить к условным вариантам.
Задача 3.
Проведите сравнительный анализ результатов педагогического эксперимента в контрольных и экспериментальных группах, используя критерий однородности Пирсона.
 , где
, где 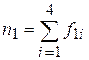 и
и 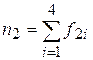 .
.
Уровень значимости положите 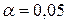
3.1.
Значение варианты 
| 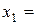 2 2
| 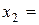 3 3
| 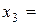 4 4
|  5 5
|
Частота появления  в экспериментальной группе в экспериментальной группе
|  9 9
| 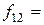 28 28
|  25 25
| 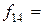 27 27
|
Частота появления  в контрольной группе в контрольной группе
|  10 10
| 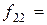 18 18
|  5 5
| 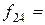 9 9
|
3.2.
Значение варианты 
| 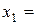 2 2
| 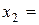 3 3
| 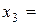 4 4
|  5 5
|
Частота появления  в экспериментальной группе в экспериментальной группе
|  8 8
| 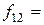 30 30
|  30 30
| 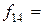 32 32
|
Частота появления  в контрольной группе в контрольной группе
|  11 11
| 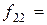 20 20
|  10 10
| 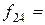 12 12
|
3.3.
Значение варианты 
| 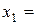 2 2
| 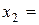 3 3
| 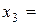 4 4
|  5 5
|
Частота появления  в экспериментальной группе в экспериментальной группе
|  7 7
| 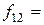 25 25
|  26 26
| 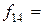 30 30
|
Частота появления  в контрольной группе в контрольной группе
|  10 10
| 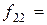 20 20
|  5 5
| 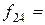 10 10
|
3.4.
Значение варианты 
| 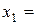 2 2
| 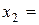 3 3
| 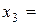 4 4
|  5 5
|
Частота появления  в экспериментальной группе в экспериментальной группе
|  5 5
| 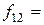 30 30
|  40 40
| 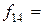 30 30
|
Частота появления  в контрольной группе в контрольной группе
|  10 10
| 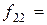 20 20
|  10 10
| 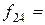 10 10
|
|
|
|
3.5.
Значение варианты 
| 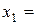 2 2
| 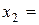 3 3
| 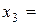 4 4
|  5 5
|
Частота появления  в экспериментальной группе в экспериментальной группе
|  10 10
| 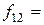 30 30
|  30 30
| 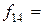 29 29
|
Частота появления  в контрольной группе в контрольной группе
|  12 12
| 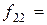 20 20
|  8 8
| 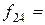 7 7
|
3.6.
Значение варианты 
| 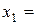 2 2
| 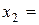 3 3
| 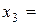 4 4
|  5 5
|
Частота появления  в экспериментальной группе в экспериментальной группе
|  7 7
| 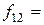 30 30
|  20 20
| 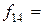 40 40
|
Частота появления  в контрольной группе в контрольной группе
|  5 5
| 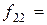 20 20
|  12 12
| 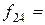 10 10
|
3.7.
Значение варианты 
| 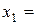 2 2
| 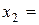 3 3
| 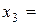 4 4
|  5 5
|
Частота появления  в экспериментальной группе в экспериментальной группе
|  6 6
| 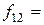 20 20
|  40 40
| 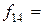 30 30
|
Частота появления  в контрольной группе в контрольной группе
|  15 15
| 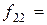 25 25
|  10 10
| 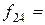 5 5
|
3.8.
Значение варианты 
| 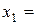 2 2
| 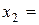 3 3
| 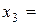 4 4
|  5 5
|
Частота появления  в экспериментальной группе в экспериментальной группе
|  8 8
| 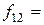 25 25
|  32 32
| 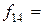 25 25
|
Частота появления  в контрольной группе в контрольной группе
|  12 12
| 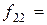 18 18
|  6 6
| 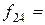 4 4
|
3.9.
Значение варианты 
| 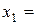 2 2
| 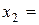 3 3
| 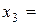 4 4
|  5 5
|
Частота появления  в экспериментальной группе в экспериментальной группе
|  12 12
| 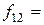 28 28
|  30 30
| 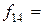 25 25
|
Частота появления  в контрольной группе в контрольной группе
|  10 10
| 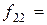 22 22
|  8 8
| 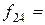 4 4
|
3.10.
Значение варианты 
| 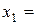 2 2
| 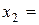 3 3
| 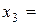 4 4
|  5 5
|
Частота появления  в экспериментальной группе в экспериментальной группе
|  10 10
| 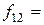 30 30
|  35 35
| 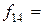 25 25
|
Частота появления  в контрольной группе в контрольной группе
|  12 12
|  18 18
|  10 10
|  6 6
|
Задача 4.
Исследуется зависимость коэффициента усвоения знаний, выраженного в процентах (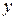 %) от уровня посещаемости занятий (
%) от уровня посещаемости занятий ( %) в группе из четырнадцати учащихся (
%) в группе из четырнадцати учащихся ( - порядковый номер учащегося). Статистические данные приведены в таблице.
- порядковый номер учащегося). Статистические данные приведены в таблице.
Требуется:
1) Найти оценки параметров линейной регрессии  на
на  . Построить диаграмму рассеяния и нанести прямую регрессии на диаграмму рассеяния.
. Построить диаграмму рассеяния и нанести прямую регрессии на диаграмму рассеяния.
2) На уровне значимости 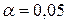 проверить гипотезу о согласии линейной регрессии с результатами наблюдений.
проверить гипотезу о согласии линейной регрессии с результатами наблюдений.
3) С надежностью 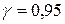 найти доверительные интервалы для параметров линейной регрессии.
найти доверительные интервалы для параметров линейной регрессии.
4.1.

| ||||||||||||||

| ||||||||||||||

|
4.2.

| ||||||||||||||

| ||||||||||||||

|
4.3.

| ||||||||||||||

| ||||||||||||||

|
4.4.

| ||||||||||||||

| ||||||||||||||

|
4.5.

| ||||||||||||||

| ||||||||||||||

|
|
|
|
4.6.

| ||||||||||||||

| ||||||||||||||

|
4.7.

| ||||||||||||||

| ||||||||||||||

|
4.8.

| ||||||||||||||

| ||||||||||||||

|
4.9.

| ||||||||||||||

| ||||||||||||||

|
4.10.

| ||||||||||||||

| ||||||||||||||

|
Задача 5.
Предположим, что в педагогическом эксперименте участвовали три группы студентов по 10 человек в каждой. В группах применили различные методы обучения: в первой – традиционный 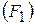 , во второй – основанный на компьютерных технологиях
, во второй – основанный на компьютерных технологиях 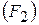 , в третьей – метод, широко использующий задания для самостоятельной работы
, в третьей – метод, широко использующий задания для самостоятельной работы  . Знания оценивались по десятибалльной системе.
. Знания оценивались по десятибалльной системе.
Требуется обработать полученные данные об экзаменах и сделать заключение о том, значимо ли влияние метода преподавания, приняв за уровень значимости 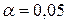 .
.
Результаты экзаменов заданы таблицей,  – уровень фактора
– уровень фактора  – оценка
– оценка  -го учащегося обучающегося по методике
-го учащегося обучающегося по методике  .
.
5.1.
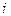
| |||||||||||
Уровень фактора

| 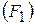
| ||||||||||
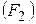
| |||||||||||

|
5.2.
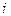
| |||||||||||
Уровень фактора

| 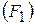
| ||||||||||
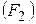
| |||||||||||

|
5.3.
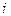
| |||||||||||
Уровень фактора

| 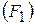
| ||||||||||
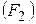
| |||||||||||

|
5.4.
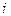
| |||||||||||
Уровень фактора

| 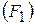
| ||||||||||
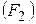
| |||||||||||

|
5.5.
|
Воспользуйтесь поиском по сайту:  ©2015 - 2026 megalektsii.ru Все авторские права принадлежат авторам лекционных материалов. Обратная связь с нами...
|

