Основные математические понятия и факты

Требования к общеобразовательной подготовке кандидата по математике.

Экзаменуемый должен:

а) знать:

- математические понятия, основные формулы и основные теоремы.

б) уметь:

- производить арифметические действия над числами, заданными в виде десятичных и обыкновенных дробей;

- производить тождественные преобразования многочленов, дробей, выражений, содержащих степенные, показательные, логарифмические и тригонометрические функции;

- решать уравнения и неравенства первой и второй степени; решать системы уравнений; решать простейшие уравнения и неравенства, содержащие степенные, показательные, логарифмические и тригонометрические функции;

- изображать геометрические фигуры на чертеже и производить простейшие построения на плоскости.

- использовать методы алгебры и тригонометрии при решении геометрических задач;

- пользоваться понятием производной при исследовании функций на возрастание (убывание), на экстремумы.

Порядок проведения письменного экзамена по математике.

До начала экзамена для кандидатов проводится консультация, где разъясняется порядок его проведения и представляемые требования.

Письменный экзамен по математике проводится по билетам, которые содержат 10 (десять) примеров по всем разделам математики школьного курса.

На письменный экзамен по математике отводится 4 астрономических часа (240 мин.).

Экзамен проводится в следующем порядке: экзаменаторы собирают экзаменационные листы кандидатов и взамен выдают титульные листы с листами – вкладышами и экзаменационные билеты. Каждый кандидат заполняет титульный лист.

Вся письменная работа как в чистовом, так и в черновом варианте выполняется только на листах – вкладышах.

После выполнения работы или по истечении времени, отведенного на письменный экзамен, титульные листы с листами – вкладышами и билеты сдаются экзаменатору.

По окончанию экзамена все письменные работы передаются ответственному секретарю для шифровки.

Проверка письменных работ производится в специально выделенном для этой цели помещении. При обнаружении на листах – вкладышах подписи или других надписей, не относящихся к работе, письменная работа проверяется двумя экзаменаторами.

Оценка по письменной работе проставляется на первой странице чистового листа-вкладыша и заверяется подписью экзаменатора. Одновременно оценка проставляется в экзаменационную ведомость с занесением в нее шифра кандидата.

По окончании проверки письменные работы передаются ответственному секретарю для расшифровки и проставления оценок в экзаменационные листы.

Исправление оценок, проставленных по результатам сдачи экзамена, допускается только с разрешения председателя приемной комиссии и оформляется протоколом заседания комиссии.

Программа по математике

На экзамене по математике поступающий в высшее учебное заведение должен показать: а) четкое знание математических определений и теорем, предусмотренных программой, умение доказывать эти теоремы; б) уме­ние точно и сжато выражать математическую мысль в устном и письменном изложении, использовать соответствующую символику; в)уверенное владение математическими знаниями и навыками, предусмотренными программой, умение применять их при решении задач.

Программа по математике для поступающих в высшие учебные заведе­ния состоит из четырех разделов. Первый из них представляет собой перечень основных математических понятий и фактов, которыми должен владеть поступающий (уметь правильно их использовать при решении задач, ссылаться на них при доказательстве теорем). Во втором разделе указаны теоремы, которые надо уметь доказывать. В третьем разделе перечислены основные математические умения, и навыки, которыми должен владеть экзаменуемый. В четвертом - типовые задания, входящие в экзаменационные билеты.

Основные математические понятия и факты

Арифметика, алгебра и начала анализа

1.Натуральные числа (N). Простые и составные числа. Делитель, кратное. Общий наибольший делитель. Общее наименьшее кратное.

2.Признаки делимости на 2, 3, 5, 9 и 10.

3.Целые числа (Z). Рациональные числа (Q), их сложение, вычита­ние, умножение и деление. Сравнение рациональных чисел.

4.Действительные числа (R), их представление в виде десятичных дробей.

5.Изображение чисел на прямой. Модуль действительного числа, его геометрический смысл.

6.Числовые выражения. Выражения с переменными, формулы сокра­щенного умножения.

7.Степень с натуральным и рациональным показателем. Арифмети­ческий корень.

8.Логарифмы, их свойства.

9.Одночлен и многочлен.

10.Многочлен с одной переменной. Корень многочлена на примере квадратного трехчлена.

11.Понятие функции. Способы задания функции, Область определе­ния, множество значений функции.

12.График функции. Возрастание и убывание функции; периодич­ность, четность нечетность.

13.Достаточное условие возрастания (убывания) функции на проме­жутке. Понятие экстремума функции. Необходимое условие экстремума функции (теорема Ферма). Достаточное условие экстремума. Наиболь­шее и наименьшее значения функции на промежутке.

14.Определение и основные свойства функций: линейной, квадратичной у = ax² + bx² + с, степенной у = aхⁿ ( n Î N), у = k/x, показательной у=а ^x, а>0, логарифмической, тригонометрических функций (у = sinx; у = cosx; у = tg х), арифметического корня у =Öx.

15.Уравнение. Корни уравнения. Понятие о равносильных уравнениях.

16.Неравенства. Решения неравенства. Понятие о равносильных не­равенствах.

17.Система уравнений и неравенств. Решения системы.

18.Арифметическая и геометрическая прогрессия. Формула n-го чле­на и суммы первых n членов арифметической прогрессии. Формула n - гочлена и суммы первых n членов геометрической прогрессии.

19.Синус и косинус суммы и разности двух аргументов (формулы).

20.Преобразование в произведение сумм sina ± sinb; cosa ± cosb.

21.Определение производной. Ее физический и геометрический смысл.

22.Производные функций у = sinx, у = cosx,

у = tg х, у = хⁿ (n Î Z); y=a ^x.

Геометрия

1.Прямая, луч, отрезок, ломаная; длина отрезка. Угол, величина угла. Вертикальные и смежные углы. Окружность, круг. Параллельные пря­мые.

2.Примеры преобразования фигур, виды симметрии. Преобразование подобия и его свойства.

3.Многоугольник, его вершины, стороны, диагонали.

4.Треугольник. Его медиана, биссектриса, высота. Виды треуголь­ников. Соотношения между сторонами и углами прямоугольного треугольника.

5.Четырехугольник: параллелограмм, прямоугольник, ромб, квадрат, трапеция.

6.Окружность и круг. Центр, хорда, диаметр, радиус. Касательная к окружности. Дуга окружности. Сектор.

7.Центральные и вписанные углы.

8.Формулы площади: треугольника, прямоугольника, параллелог­рамма, ромба, квадрата, трапеции.

9.Длина окружности и длина дуги окружности. Радиальная мера угла. Площадь круга и площадь сектора.

10.Подобие. Подобные фигуры. Отношение площадей подобных фи­гур.

11.Плоскость. Параллельные и пересекающиеся плоскости.

Основные формулы и теоремы

Алгебра и начала анализа

1.Свойста функции у=ах+b и ее график.

2.Свойства функции у = k/x и ее график.

3.Свойства функции у = ах² + Ьх + с и ее график.

4.Формула корней квадратного уравнения.

5.Разложение квадратного трехчлена на линейные множители.

6.Свойства числовых неравенств.

7.Логарифм произведения, степени, частного.

8.Определение и свойства функций у = sinx и у = cosx и их графики.

9.Определениеи свойства функции у = tgx и ее график.

10.Решение уравнений вида sinx= a, cosx= a, tgx= а.

11.Формулы приведения.

12.Зависимости между тригонометрическими функциями одного и того же аргумента.

13.Тригонометрические функции двойного аргумента.

14.Производная суммы двух функций.

Геометрия

1.Свойства равнобедренного треугольника.

2.Свойства точек, равноудаленных от концов отрезка.

3.Признаки параллельности прямых.

4.Сумма углов треугольника. Сумма внутренних углов выпуклого многоугольника.

5.Признаки параллелограмма.

6.Окружность, описанная около треугольника.

7.Окружность, вписанная в треугольник.

8.Касательная к окружности и ее свойство.

9.Изменение угла, вписанного в окружность.

10.Признаки подобия треугольников.

11.Теорема Пифагора.

12.Формулы площадей параллелограмма, треугольника, трапеции.

13.Формула расстояния между двумя точками плоскости. Уравнение окружности.

Основные умения и навыки

Экзаменующийся должен уметь:

1.Производить арифметические действия над числами, заданными в виде десятичных и обыкновенных дробей; с требуемой точностью округ­лять данные числа и результаты вычислений.

2.Проводить тождественные преобразования многочленов, дробей, со­держащих переменные, выражений, содержащих степенные, показатель­ные, логарифмические и тригонометрические функции.

3.Строить графики линейной, квадратичной, степенной, показатель­ной, логарифмической и тригонометрической функций.

4.Решать уравнения и неравенства первой и второй степени, уравне­ния и неравенства, приводящиеся к ним; решать системы уравнений и неравенств первой и второй степени и приводящиеся к ним. Сюда, в частности, относятся простейшие уравнения и неравенства, содержащие степенные, показательные, логарифмические и тригонометрические фун­кции.

5.Решать задачи на составление уравнений и систем уравнений.

6.Изображать геометрические фигуры на чертеже и производить про­стейшие построения на плоскости.

7.Использовать геометрические представления при решении алгебра­ических задач, а методы алгебры и тригонометрии—при решении геомет­рических задач.

8.Пользоваться понятием производной при исследовании функций на возрастание (убывание), на экстремумы и при построении графиков фун­кций.

Типовые задания.

Вычислить:

 

 

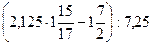Решить систему уравнений:

 

Вычислить:

f'(x) при x=0, если: f(x)=sinx+3x+5x² f(x)=3x²+3x+5

f(x)=5x³+4cosx+21 f(x)=2x⁵+3sinx+2x f(x)=3x⁴+4sinx+5x

 

Вычислить производную функции:

 

Решить неравенство:

lg(x+3)>lg(29-3x) log_1/2(2x-1)>log_1/2(x+1)

log₃(1-x)>log₃(3-2x) log₃(3x-4)>log₃(x-2)

lg2x<lg(x-1)

 

Решить уравнение:

|5x-2x|+|x-3|=2 |2-x|=|2x+1|

|x+3|=|2x-1| |x-2|+|x+2|=4

|2x-5|=|x|

Решить уравнение:

sin2x=sinx 2^3x=4^2x+1

3^x+5-20 ^. 3^x+2=63 sin2x=cos6x

sin7x=cos4x

 

Найти экстремумы функции:

f(x)=x³-12x f(x)=-x²-8x+13

f(x)=4x²+8x+17 f(x)=3x²+6x+8

f(x)=4x²-4x+2

 

Стороны двух смежных сторон квадрата соединены между собой и с противоположной вершиной квадрата. Площадь полученного треугольника равна 54. Определить сторону квадрата.

Катеты прямоугольного треугольника равны 3 и 4. Найти радиус вписанной окружности.

Найти площадь прямоугольного треугольника с острым углом 30⁰ и гипотенузой 5.

В равнобедренном треугольнике основание 6. Найти боковую сторону, если медиана, опущенная на известную сторону, равна 4.

Определить площадь полной поверхности цилиндра, осевое сечение которого есть квадрат, а боковая поверхность равна S.

 

Упростить выражение:

 

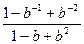Поделиться:

Воспользуйтесь поиском по сайту: