 |
По дисциплине «Математический анализ»
|
|
|
|
Вопросы для подготовки к экзамену
1. Понятие множества.
2. Абсолютная величина действительного числа.
3. Окрестность точки.
4. Понятие функции.
5. Основные свойства функций.
6. Основные элементарные функции.
7. Элементарные функции.
8. Классификация функций.
9. Преобразование графиков.
10. Применение функций в экономике.
11. Интерполирование функций.
12. Предел числовой последовательности.
13. Предел функции в бесконечности и в точке.
14. Бесконечно малые величины.
15. Бесконечно большие величины.
16. Основные теоремы о пределах.
17. Признаки существования предела.
18. Замечательные пределы.
19. Задача о непрерывном начислении процентов.
20. Непрерывность функции.
21. Определение производной.
22. Зависимость между непрерывностью и дифференцируемостью функции.
23. Схема вычисления производной.
24. Основные правила дифференцирования.
25. Производная сложной и обратной функций.
26. Производные основных элементарных функций.
27. Понятие о производных высших порядков.
28. Экономический смысл производной.
29. Использование понятия производной в экономике.
30. Основные теоремы дифференциального исчисления.
31. Правило Лопиталя.
32. Возрастание и убывание функций.
33. Экстремум функции.
34. Наибольшее и наименьшее значения функции на отрезке.
35. Выпуклость функции.
36. Точки перегиба.
37. Асимпоты графика функции.
38. Общая схема исследования функций и построения их графиков.
39. Приложение производной в экономической теории.
40. Понятие дифференциала функции.
41. Применение дифференциала в приближенных вычислениях.
42. Понятие о дифференциалах высших порядков.
43. Первообразная функция и неопределенный интеграл.
|
|
|
44. Свойства неопределенного интеграла.
45. Интегралы от основных элементарных функций.
46. Метод замены переменной.
47. Метод интегрирования по частям.
48. Интегрирование простейших рациональных дробей.
49. Интегрирование некоторых видов иррациональностей.
50. Интегрирование тригонометрических функций.
51. Об интегралах «неберущихся» в элементарных функциях.
52. Понятие определенного интеграла, его геометрический и экономический смысл. Свойства определенного интеграла.
53. Определенный интеграл как функция верхнего предела.
54. Формула Ньютона-Лейбница.
55. Замена переменной и формула интегрирования по частям в определенном интеграле.
56. Геометрические приложения определенного интеграла.
57. Несобственные интегралы.
58. Приближенное вычисление определенного интеграла.
59. Использование понятия определенного интеграла в экономике.
60. Основные понятия.
61. Сходимость ряда.
62. Необходимый признак сходимости.
63. Гармонический ряд.
64. Ряды с положительными членами.
65. Ряды с членами произвольного ряда.
66. Область сходимости Ряд Маклорена.
67. Применение рядов в приближенных вычислениях.
68. Основные понятия.
69. Предел и непрерывность.
70. Частные производные.
71. Дифференциал функции.
72. Производная по направлению.
73. Градиент.
74. Экстремум функции нескольких переменных.
75. Наибольшее и наименьшее значения функции.
76. Условный экстремум.
77. Метод множителей Лагранжа.
78. Понятие об эмпирических формулах.
79. Метод наименьших квадратов.
80. Понятие двойного интеграла.
81. Функции нескольких переменных в экономической теории.
Пример экзаменационного билета
Билет №1
1. Интеграл Римана и его свойства.
2. Дифференциал функции многих переменных.
3. Найти интеграл ∫ arcsin(x)dx.
4. Вычислить первый и второй дифференциалы функции f(x, y) = exy.
5. Найти экстремумы функции f(x,y) = xy при условии x2 + y2 = 1.
При выполнении экзаменационного задания требуется решить задачи, сформулировать соответствующие определения и теоремы и привести доказательство одной из них по выбору студента.
|
|
|
Тематика контрольных работ
Задачи контрольной работы
по дисциплине «Математический анализ»
Задание №1. Вычислить пределы:
1.
2.
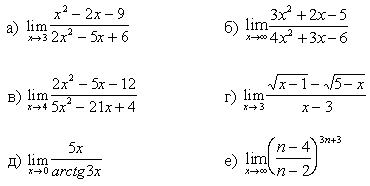
3.
4.
5.
6.
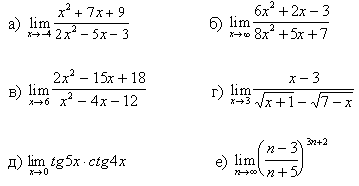
7.
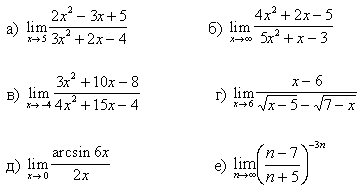
8.
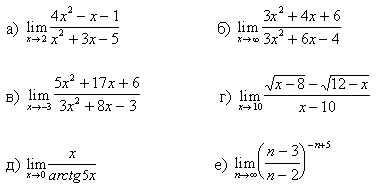
9.
10.
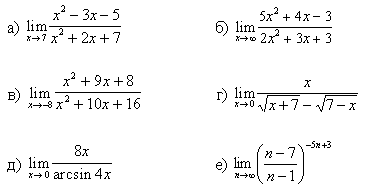
Задание №2. Найти производные заданных функций:
1.
2.
3.
4.
5.
6.
7.
8.
9.
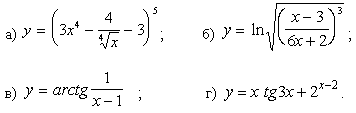
10.
Задание №3. Исследовать средствами дифференциального исчисления исследовать функцию y = f(x) и построить ее график.
1. y = x3 - 9x2 + 24x - 16
2. y = x3 -11x2 + 39x - 45
3. y = x3 + 6x2 + 9x + 4
4. y = x3 + x2 - 5x + 3
5. y = x3 + 10x2 +32x + 32
6. y = x3 + 9x2 + 24x + 20
7. y = x3 - 14x2 + 60x - 72
8. y = x3 - 12x2 + 45x - 54
9. y = x3 - 18x2 + 105x -196
10. y = x3 - 10x2 + 28x - 24
Задание №4. Вычислить приближенное значение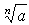 
, заменяя приращение функции 
дифференциалом.
| 1. n=3, a=125,93 | 6. n=4, a=255,16 |
| 2. n=5, a=242,05 | 7. n=3, a=124,07 |
| 3. n=4, a=256,96 | 8. n=5, a=243,95 |
| 4.n=3, a=216,99 | 9. n=4, a= 81,84 |
| 5. n=5, a= 32,85 | 10. n=3, a=215,04 |
|
|
|
