Выбор оптимальной длины кодовой комбинации при использовании циклического кода в системе с РОС

Длина кодовой комбинации n должна быть выбрана таким образом, чтобы обеспечить наибольшую пропускную способность канала связи. При использовании корректирующего кода кодовая комбинация содержит n разрядов, из которых к разрядов являются информационными, а r разрядов - проверочными: n = k+r;

Если в системе связи используются двоичные сигналы (сигналы типа 1 и 0 ) и каждый единичный элемент несет не более одного бита информации, то между скоростью передачи информации и скоростью модуляции существует соотношение:  C = k/n×B                                                                  

где С - скорость передачи информации, бит/с,

В - скорость модуляции. Бод.

Очевидно, что чем меньше r, тем больше отношение k/n приближается к 1, тем меньше отличается С от В, т.е. тем выше пропускная способность системы связи.

Известно также, что для циклических кодов с минимальным кодовым расстоянием d0=3 справедливо соотношение:

                                          r ³ log (n+1);                                                        

С точки зрения внесения постоянной избыточности в кодовую комбинацию выгодно выбирать длинные кодовые комбинации, так как с увеличением n относительная пропускная способность:                                   R = C/B = k/n;                                                     

увеличивается, стремясь к пределу равному 1.

В реальных каналах связи действуют помехи, приводящие к появлению ошибок в кодовых комбинациях. При обнаружении ошибки декодирующим устройством в системах с РОС производится переспрос группы кодовых комбинаций. Во время переспроса полезная информация не передается, поэтому скорость передачи информации уменьшается.

  В этом случае: 

                            C = B k/n[1- Poo(M+1)/Pпп+Poo(M+1)]                            

где Pоо - вероятность обнаружения ошибки декодером (вероятность переспроса);

Рпп - вероятность правильного приема (безошибочного приема) кодовой комбинации;

М - емкость накопителя передатчика в числе кодовых комбинаций.

При малых вероятностях ошибки в канале связи (Рош<0.005) вероятность Роо также мала, поэтому знаменатель мало отличается от 1 и можно считать:

                                C»B×k/n[1-Poo(M+1)];                                                   

При независимых ошибках в канале связи, при n×Рош<<1

                                    Poo» n×Poш;                                                                  

тогда                           C» B×k/n[1-n×Poш(M+1)];                                          

Емкость накопителя M= [3+2×tp/tкомб];                                                      

где        tр-время распространения сигнала по каналу связи, с

tкомб - длительность кодовой комбинации из n разрядов, с

Но       tp = L/v;          tкомб = n/B;

После подстановок имеем      R = k/n[1-Poш (4n+2LB/v)];                       (1)

При наличии ошибок в канале связи величина R является функцией Рош, n, k, L, В, v. следовательно, существует оптимальное n при котором относительная пропускная способность будет максимальной.

Формула (1) еще более усложняется в случае зависимых ошибок в канале связи (при пакетировании ошибок).

Выведем эту формулу для модели ошибок Пуртова. Необходимо определить вероятность:  

Р(³tоб,n) = (n/ tоб) × Pош = (n/do-1) ×Pош

Рно»1/2 ×P(³tоб, n);                                          

Подставляя значение заменой tоб на dо-1, имеем

                              r = {3.32[(1-a)×lg n/dо-1+lg Pош - lg Pно]}      (2)

Окончательно 

R = {1-3.32/n [(1-a)×lg n/d0-1+lg Pош - lg Pно]}× 1- Pош ×n (4+2LB/vn)      (3)

 

К параметрам циклического кода относятся:

    n- длина кодовой комбинации;

 k- длина информационной части кодовой комбинации;

 r- длина проверочной части кодовой комбинации;

 

Определим оптимальную длину кодовой комбинации n, обеспечивающую наибольшую относительную пропускную способность R и число проверочных разрядов r обеспечивающих заданную вероятность необнаруженной ошибки Рош при заданной кратности ошибок tоб внутри кодовой комбинации и заданной вероятности ошибок Рош в канале связи.

По результатам расчетов составляем таблицы для Рош = 0,0005 и Рош = 0,005:

L=5500 км; a=0.55; a0=4; V=80000; B=1200 Бод; Рно=3.0×10-6

 

n=2 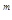-1,где m=5...12

R = {1-3.32/n [(1-a)×lg n/d0-1+lg Pош - lg Pно]}× 1- Pош ×n (4+2LB/vn)      

r = {3.32[(1-a)×lg n/dо-1+lg Pош - lg Pно]}          

k=n-r

 

Таблица 1                     Рош = 0,0005                                

R	n	r	k
0.69758	31	9	22
0.83337	63	10	53
0.90115	127	10	117
0,93277	255	11	244
0.94402	511	11	500
0.94254	1023	12	1011
0.93163	2047	12	2035
0.91202	4095	13	4082

 

nопт=511

Из таблицы 1 видно, что наибольшую пропускную способность R=0.94402 обеспечивает циклический код с параметрами n= 511, r= 11. k=500

 

 

    

Таблица 1                     Рош = 0,005                                

R	n	r	k
0.47359	31	13	18
0.62827	63	13	50
0.6865	127	14	113
0,68048	255	14	241
0.62465	511	15	496
0.52192	1023	15	1008
0.36679	2047	15	2032
0.14655	4095	16	4079

 

nопт=127

Из таблицы 2 видно, что наибольшую пропускную способность R= 0,6865 обеспечивает циклический код с параметрами n= 127, r= 14 k=113.

    

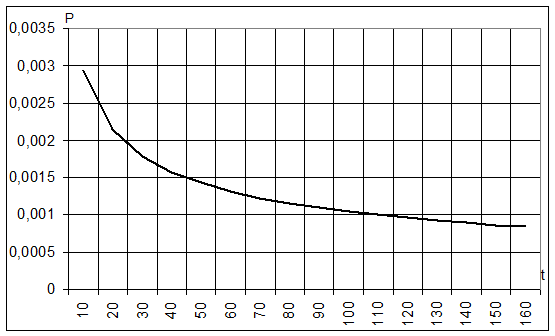
Для полученой длинны блока построить граф розделения вероятности кратности ошибки.

Граф вероятностей P(t,n=n опт).

t£n/3

n=n оптимальный

n=511 P=0.0005

n=127 P=0.005

 

12	Поделиться:

Воспользуйтесь поиском по сайту: