 |
Энергия магнитного поля катушки с током.
|
|
|
|
Энергия магнитного поля катушки с током.
Работа магнитного поля идет на превращение механической энергии движения частиц в электрическую энергию тока. Энергию магнитного поля катушки можно определить по формуле: 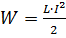 .
.
Эта формула достаточно просто запоминается, если произвести аналогию с механикой. В данном случае характеристикой рассматриваемого объекта является индуктивность, аналогичная массе. А скорость тела в механике аналогична силе тока.
ЛЕКЦИЯ 4. Электромагнитные колебания и волны.
Как уже говорилось в курсе механики, колебания - это изменение состояния системы. Электромагнитные колебания предполагают изменение тока, заряда или же напряжения. В школьном курсе физики такого типа колебания рассматриваются на примере колебательного контура. Данные изменения происходят в конденсаторе и в катушке. Электромагнитные колебания в контуре происходят только за счет энергии, которая сберегается в конденсаторе и катушке, без посторонней силы. Принято считать, что в катушке сопротивление отсутствует. Время, за которое происходит одно колебание, будем считать равным 1 периоду.

В начальный момент на конденсаторе сохранен заряд размером q0. После этого ток начнет постепенно перемещаться на катушку, однако, моментально принять максимальное значение он не может, поэтому происходит его изменение, в результате чего изменяется магнитное поле и тем самым появляется самоиндукция. Она, в свою очередь, пытается противодействовать возрастанию тока, поэтому так же увеличивается.
Чтобы стало более понятно, давайте представим пружинный маятник. В начальный момент пружина растянута до максимального значения. В это время скорость его является нулевой, однако в тот момент, когда маятник отпускают, он начинает ускоряться благодаря силам упругости, но, чем ближе к нерастянутому положению, тем меньше данная скорость становится.
|
|
|
Итак, по истечению первой четверти периода катушка максимально наполняется током, а конденсатор, наоборот, отдал весь заряд. На протяжении второй четверти заряд переходит на конденсатор и снова постепенно его заряжает. Следует отметить, что не происходит моментально зарядки или разрядки конденсатора - заряд с него уходит постепенно.

Во время перезарядки конденсатора обкладки наполняются зарядом, противоположным первоначальному. Полностью конденсатор перезаряжается только по прошествии первой половины периода. После этого происходят такие же изменения в контуре, но в обратном направлении.

И когда обкладки конденсатора полностью зарядятся точно так же, как и было в начальный момент времени - пройдет период.
Если в контуре отсутствует сопротивление, то такие колебания будут продолжаться бесконечно долго, без изменения амплитуды. Если же рассматривать подобную цепь в реальной жизни, то за каждый период на конденсатор будет возвращаться меньшее количество заряда, поэтому величина тока будет постепенно падать. В конечном итоге, из-за сопротивления он полностью потухнет.
Гармонические колебания.
Колебания в идеальном контуре можно описать с помощью законов синуса и косинуса. При этом ток - производная заряда.
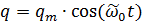 ,
,  , где
, где
q и qm – мгновенное и максимальное значения заряда конденсатора,
I и Im – мгновенное и максимальное значения силы тока,
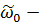 циклическая частота колебаний.
циклическая частота колебаний.
При рассмотрении колебаний в механике мы рассматривали, что на период колебаний математического маятника влияет длина нити и ускорение свободного падения, в пружинном маятнике - масса груза и жесткость пружины. В данном случае основными величинами, которые влияют на период, являются емкость конденсатора и индуктивность. Формула для нахождения периода называется формулой Томсона:
|
|
|
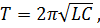
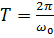 ,
, 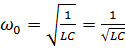 .
.
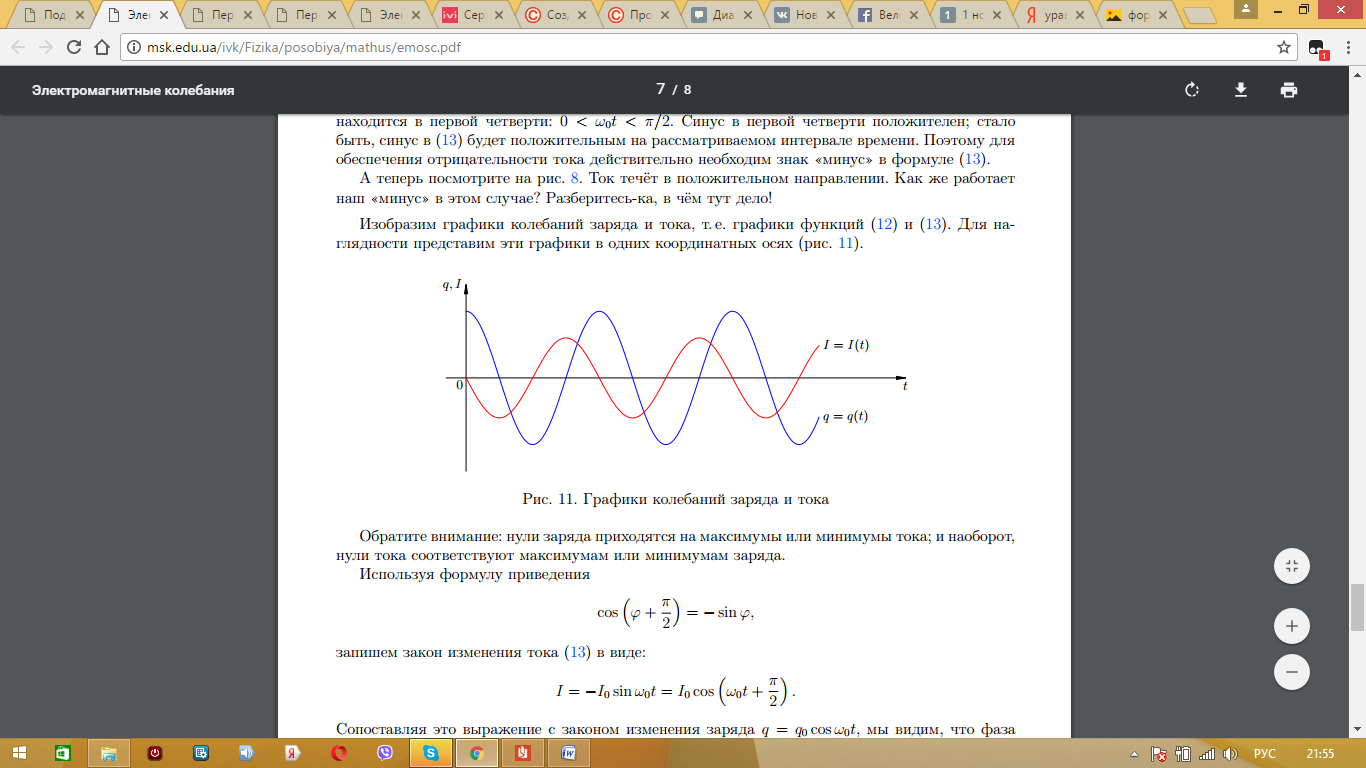
Во время колебаний в колебательном контуре происходит переход заряда из конденсатора в катушку и обратно. В каждой из частей такого контура электромагнитное поле совершает определенную работу. Поэтому для такого перемещения заряда и тока необходима энергия. Так же, как и в случае с описанием каждой части периода, так и с энергией имеется такая же зависимость. В момент, когда максимальный заряд находится на конденсаторе, он имеет максимальное значение энергии, а энергия на катушке равна нулю. После того, как весь ток перешел на катушку - энергия катушки максимальна, а на конденсаторе равна нулю. Но все мы знаем, что в природе существует закон сохранения заряда. Поэтому максимальное значение энергии на конденсаторе равно максимальной энергии на катушке. Максимальная энергия конденсатора: 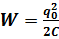 .
.
|
|
|


