Задания по оптике. Выполнил Фунтов А.А. студент 211гр. ФНП.

№1

Частота современных мобильных телефонов лежит в диапазоне от 1.7 ГГц до 1.9ГГц.

№2

Формулы МаксвеллаФ в интегральной форме имеют вид:

1) , которая по существу является обобщенным законом Фарадея

2) Это уравнение показывает, тот факт, что магнитное поле создается как движущимися зарядами, так и переменным электрическим полем

3)

4) формулы 3 и 4 являются выражением теоремы Остроградского-Гаусса. Физический смысл 3 в том, что электрические поля создаются зарядами, а 4 в том, что магнитных зарядов в природе не существует. Фактически первые два уравнения связывают электрические и магнитные поля.

Вывод волнового уравнения:

Воспользуемся дифференциальным видом уравнений 1и 2, а именно:

и 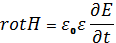. Возьмем ротор от первого уравнения:

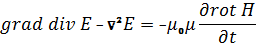(5).

Так как grad div =0, получим при подстановке 2-го уравнения в (5):

.

Приняв , получим:

.

Аналогично для магнитного поля:

№3

Подставим уравнение сферической волны () в волновое получим:

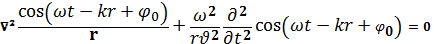
№4

Подставим уравнение плоской волны в комплексном виде() в волновое уравнение. Получим:

так как имеем дело с монохроматической волной и под скоростью в уравнении понимается фазовая скорость ().

№5

Подставим уравнение плоской волны в комплексном виде ( и ) в уравнения Максвелла получим:

Умножим полученные уравнения друг на друга скалярно, получим:

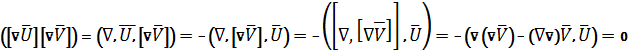
Очевидно, что вектора перпендикулярны и, следовательно, вектор Умова-Пойтинга () показываЗющий направление распространения волны так же перпендикулярен векторам . Последнее показывает тот факт, что электромагнитная волна поперечна. А так как вектор тоже показывает направление распространения волны, то он сонаправлен с вектором Умова-Пойтинга, а, следовательно, составляет с векторами правую тройку векторов.

Поскольку переменное электрическое поле порождает переменное магнитное поле и наоборот, так как свет может преодолевать большие расстояния, то вектора в бегущей волне сфазированны.

Рассмотрим случай распространения плоской волны вдоль положительного направления оси х. Вектора Е=Е(t-x/v) и H=H(t-x/v) направлены вдоль осе x и z соответственно. В этом случае уравнения Максвелла можно переписать в следующем виде

Введя обозначение α= t-x/v

Подставив полученное в 1-ое уравнение.

С учетом

получим:

 

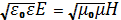
№6

Найти спектр колебаний волнового цуга конечной длительности τ_с

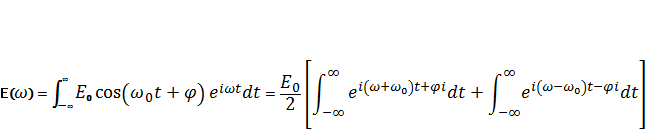
№7

Выведем закон отражения из принципа Гюйгенса. Рассмотрим преломление лучей света на границе раздела 2-х сред.

Пусть луч пришел в точку А (в дальнейшем луч 1) в момент времени t₀, и отразивший дошел до некой точки D за время Δt, находящейся на луче прошедшем за Δt расстояние между точками В и С(в дальнейшем луч 3). Так как скорость лучей одинакова то пройденные за время Δt отрезки АD и ВС равны. Отрезок АВ перпендикулярен лучам 1-3. Отрезок АD получим проведя перпендикулярную линию, проходящей через фронт отраженной волны из точки А и огибающей всех фронтов (из точек А и С), построенной по принципу Гюйгенса. Так как АВ перпендикулярен лучу 1, то угол ВАС равен α₀ и угол АВС, а так же АВD прямой. Отрезки АD и ВС равны и угол …

 

№8

Построим графики для коэффициентов отражения.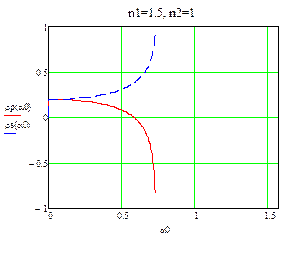

№9

Рассмотрим ситуацию на рис. Докажем, что

Так как коэффициенты отражения и преломления

выводятся из отношений напряженностей света

отраженного, преломленного и падающего

соответственно (т.е. ), достаточно доказать равенство

Из формул Френеля следует, что

№10

Получим уравнения для фазовых сдвигов при полном внутреннем отражении. Воспользуемся формулами Френеля

Так как косинус угла преломления комплексное число

и отражение полное, то

 

Числитель и знаменатель в формулах Френеля в данном случае можно представить как комплексно сопряженные числа, т.е.

 

Следовательно: и

 

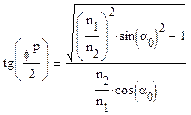
Аналогично для s компоненты

Так как , то найдем формулу для разности фаз из формулы для тангенса от разности углов.

 

Подставив нетрудно получить

Построим графики для n₁=1.5, n₂=1.

 

№11

Выведем закон отражения из принципа Гюйгенса. Пусть на ровную поверхность под углом α₀ падают 3 луча (см.рис). Первым до поверхности дошел луч 1, в этот же момент времени луч 3 был в точке В. Далее по принципу Гюйгенса образовалась огибающая всех волновых фронтов образовавшихся за время, требуемое на прохождение ВС. Эта огибающая соединяет точки D (АD- 1 луч отраженный от поверхности) и C. Очевидно, что АD перпендикулярен CD, также как АВ к ВС. Поскольку на преодоление отрезков АВ и АD свет потратил одно и тоже время, то они равны. То есть имеем два прямых и равных (по гипотенузе и катету) треугольника АDС и СВА, следовательно углы при равных катетах равны, т.е. углы САD и ВСА равны. Ясно, что угол САD= , так как лучи 1и 3паралельны, следовательно угол между вертикалью и АD равен α₀.

№12

Выведем закон Брюстера из уравнения Френеля. Явления Брюстера заключается в том, что при определенном угле падения свет не отражается, т.е. , что можно переписать в виде:

Очевидно, что должно выполняться

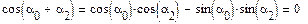
Т.к. из физических соображений. Из законов преломления ясно, что

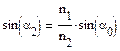и

Подставим эти выражения в полученное уравнение, получим:

Перенесем второе слагаемое вправо и возведем обе части уравнения в квадрат, получим:

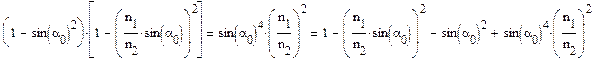
Преобразуя, получим:

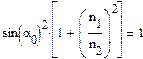
Иначе:

При угле очевидно

Из основного тригонометрического тождества:

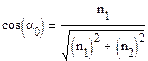
А, следовательно:

Последнее выражение и есть искомый закон Брюстера.

n2

θ

№13

n1

α

Определим формулу для числовой апертуры волокна

при заданных n₁и n₂. Запишем закон преломления для луча

Входящего из воздуха в среду с показателем преломления n₁.

Свет распространяясь в волокне испытывает явление полного внутреннего отражения и угол падения будет равен . Ясно, что угол θ_max связан с предельным углом, то

Совершив простые математические преобразования ясно, что

№14

Опишем процесс поворота плоскости поляризации при прохождении полуволновой пластины. Пусть на пластику падает линейно поляризованная волна под углом θ. В пластинке она разделяется на обыкновенную (Е_о) и необыкновенную (Е_е) с разными амплитудами. Разность фаз между ними на выходе будет равна:

 

Е0

где показатели преломления обыкновенной и

необыкновенной

θ

Ее

θ

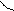
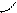
волны соответственно, а 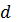длина пластины.

Так как пластина полуволновая должно выполнятся условие: 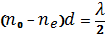, а, следовательно , следовательно Е_о и Е_е будут в противофазе. Так как Е_о и Е_е в противофазе, то выходящая волна будет повернута на угол θ относительно вертикали, но в других четвертях, а следовательно плоскость поляризации выходной волны будет повернута относительно входной на 2θ.

Если на полуволновую пластину падает эллиптическая волна, то эллиптическая волна также разделится на две волны, т.к. эллиптическую волну можно представить в виде суперпозиции 2-х волн с разностью фаз в . Для определенности пусть 1-ая волна идет как бы впереди 2-й, что обуславливает вращение вектора поляризации по часовой стрелке. Поскольку на выходе фазе изменится на , то разность фаз станет например 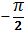, т.е. 2-я волна пойдет раньше 1-й, а, следовательно направление вращения сменится на противоположное.

 

№14

Найдем значение интенсивности света проходящего через поляроид, фазовую пластину и через другой поляроид. Пусть естественный свет падает на первый поляроид с интенсивностью I₀. Пройдя через поляроид свет станет линейно поляризованным и его интенсивность уменьшимся в 2 раза. Пройдя через фазовую пластину свет станет эллиптически поляризованным, который можно представить в виде суперпозиции двух линейно поляризованных волн: обыкновенной и необыкновенной, угол между которыми равен α, а разность фаз между которыми вычисляется по формуле:

где показатели преломления обыкновенной и необыкновенной волны соответственно, 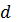длина пластины, λ длина волна света. Интенсивность света обыкновенной и необыкновенной волн равна соответственно, так как линия поляризации необыкновенной волны параллельна оптической оси. Если ось второго поляроида составляет угол θ с осью фазовой пластины, интенсивность волн прошедших через последнюю найдем из:. Поскольку из поляроида выходит линейно поляризованная волна, то световая волна будет результатом интерференции волн с интенсивностью и . Тогда из формулы для интерференции

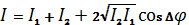
найдем интенсивность света вышедшего из второго поляроида

 

 

№15

Откуда при отраженном свете на лазерном диске появляется цветовая окраска? Это по сути своей дифракционная решетка, состоящая из круговых дорожек, состоящих из неоднородно расположенных вершин и низин, выжженных лазером, следовательно, свет, отраженный от диска испытает явление дифракции, а поскольку белый свет состоит из смешения волн с различными длинами, то для каждой конкретной волны картина дифракции будет своя, то можно наблюдать различную цветовую окраску под различными углами падения.

Измерим дифракционной угол диска от лазерной указки с длиной волны 0.65 мкм. Для этого достаточно найти угол из условия первого главного максимума. По результатам измерения он равен ≈ 0.42 радиан или 24.21^о. отсюда нетрудно найти период этой дифракционный решетки, который равен расстоянию между дорожками диска и равен ≈1.6 мкм.

№16

Определим длину когерентности белого света. Для этого будем считать, что его длина волны равна приблизительно 550 нм, а ширину определим из кривой видимости (см.рис) на уровне 0.5. Она равна ≈ 100 нм.

Найдем длину когерентности из формулы:

 

 

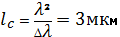
Поделиться:

Воспользуйтесь поиском по сайту: