 |
Магнитное поле в вакууме и веществе
|
|
|
|
Введение
Практические занятия являются одной из важнейших компонент учебного процесса по физике. Они способствуют приобщению студентов к самостоятельной работе, учат анализировать изучаемые физические явления, использовать на практике полученные теоретические знания.
Предназначены для студентов, изучающих раздел курса общей физики «Электричество и магнетизм». В пособии представлены примеры решения типичных задач разной степени трудности. Решения сопровождаются необходимыми указаниями и комментариями. Задачи систематизированы по основным темам раздела. По каждой теме приведены основные формулы, облегчающие усвоение алгоритмов решения задач.
Электричество и магнетизм
Электростатическое поле в вакууме
Основные формулы:
Закон Кулона:  ,
,
где 






 | |||||
 | |||||
 | |||||
 q 1 r q 2 q 1 r q 2
q 1 r q 2 q 1 r q 2
Напряженность электрического поля: 
Напряженность поля точечного заряда: 
Напряженность поля заряженного шара: 
где R — радиус шара.



Принцип суперпозиции электрических полей: 
Поток вектора напряженности через поверхность S:

Теорема Гаусса:  ,
,
где Ф Е – поток вектора напряженности через замкнутую поверхность S, q – заряд, заключенный внутри поверхности S.
Линейная плотность заряда: 
Поверхностная плотность заряда: 
Объемная плотность заряда: 
Напряженность поля, создаваемого бесконечной равномерно заряженной плоскостью, нитью:

Электрическое смещение: 
Потенциал электрического поля: 
Потенциал поля точечного заряда: 
Потенциал поля заряженного шара: 
Работа по перемещению заряда в электрическом поле: А = q (j1 - j2),
|
|
|
где (j1 - j2) — разность потенциалов.




Энергия заряженного конденсатора 
Энергия системы точечных зарядов: 
Электрический момент диполя: 





Механический момент, действующий на диполь в электрическом поле:  Поляризованность диэлектрика:
Поляризованность диэлектрика: 
Связь поляризованности и напряженности электрического поля:  , где χ – диэлектрическая восприимчивость.
, где χ – диэлектрическая восприимчивость.
Примеры решения задач
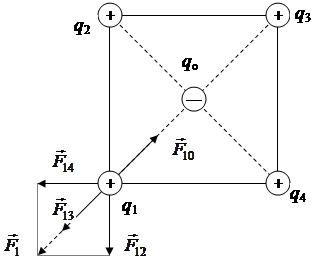 Задача 1. В центре квадрата, в каждой вершине которого находится заряд равный 2,4 нКл, помещен отрицательный заряд q o. Найти этот заряд, если на каждый заряд в вершине действует результирующая сила, равная 0,4 мН. Сторона квадрата 1 см.
Задача 1. В центре квадрата, в каждой вершине которого находится заряд равный 2,4 нКл, помещен отрицательный заряд q o. Найти этот заряд, если на каждый заряд в вершине действует результирующая сила, равная 0,4 мН. Сторона квадрата 1 см.
| Дано: а = 1см =10—2м. q 1 = q 2 = q 3 = q 4 = 2,4 нКл = 2,4 . 10—9Кл F =0,4мН=0,4 . 10—3Н | Решение. |
| q o —? |
Результирующая сила F, действующая на каждый из зарядов, находящихся в
вершинах квадрата, равна 

 ,
,

Отсюда:

Задача 2. Два заряда q 1 = q и q 2 = -4 q находятся на расстоянии r = 10 см друг от друга. Третий заряд q 3 может перемещаться только вдоль прямой, проходящей через заряды. Определите положение заряда q 3 , при котором он будет находиться в равновесии.
| Дано: q 1 = q; q 2 = -4 q; r = 10см | Решение.
Заряд будет находиться в равновесии, если  Из рисунка видно, что это условие может быть выполнено лишь на рис. (а).
Из рисунка видно, что это условие может быть выполнено лишь на рис. (а).
|
| х —? |
 |
Расстояние от меньшего по модулю заряда q 1 до q 3 на рис. (а) обозначим через х. Тогда расстояние от заряда q 2 до заряда q 3 будет равно (r + x).
Выражая в условии равновесия силы F 1 и F 2 в соответствии с законом Кулона, получим

Физическому условию задачи удовлетворяет корень х 1 = r.
Ответ: х = r.
Задача 3. Электрическое поле создано двумя точечными зарядами q 1=30 нКл и q 2=-10 нКл Расстояние d между зарядами равно 20 см. Определите напряженность электрического поля в точке, находящейся на расстоянии r 1=15 см от первого и на расстоянии r 2=10 см от второго заряда.
|
|
|
| Дано: q 1 = 30 нКл = 3 . 10-8 Кл; q 2 = -10 нКл = -10 . 10-8 Кл; d = 20 см = 0,2м; r 1 = 15 см = 0,15 м; r 2 = 10 см = 0,1 м; | Решение.
 α
α
 α
α  q 1 d q 2
q 1 d q 2
|
| Е —? |
Согласно принципа суперпозиции:

Задача 4. Заряд q =1,5 . 10—8 Кл равномерно распределен по кольцу радиуса R =0,2м. Найдите напряженность электрического поля в точке, находящейся на оси кольца на расстоянии h =0,15 м от его центра.
| Дано: q =1,510-9 Кл R =0,2 м h =0,15 м | Решение. Заряд q не является точечным, поэтому кольцо разбивается на элементарные части, заряд dq, которые можно считать точечными. |
| E —? |

 |
Согласно принципа суперпозиции:  Вектор d
Вектор d  можно разложить на составляющие dEix и dEiy . Тогда
можно разложить на составляющие dEix и dEiy . Тогда  ,
,  — единичные вектора (орты).
— единичные вектора (орты).
Очевидно, что 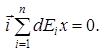 Таким образом
Таким образом  .
.
dEiy = dEi ·cosα, 

Ответ: E =1,3·103 (В/м).
Задача 5. Заряд точечный q о = —2×10—10 Кл расположен на продолжении оси диполя, электрический момент которого р е = —1,5×10—10 Кл×м, на расстоянии r =10 см от его центра (ближе к положительному заряду диполя). Какую работу надо совершить, чтобы перенести этот заряд в симметрично расположенную точку по другую сторону диполя.
 Дано:
q о = -2. 10-10 Кл
р е = -1,5 . 10-10 Кл. м,
r = 10 см Дано:
q о = -2. 10-10 Кл
р е = -1,5 . 10-10 Кл. м,
r = 10 см
| Решение. Работа А *, совершаемая внешними силами при перемещении заряда в электрическом поле, равна работе |
| А *—? | сил поля, взятой с обратным знаком. |

где j1 и j2 - потенциалы точек В и С.

Если учесть, что  и при r >>
и при r >>  выражениями
выражениями  в знаменателе можно пренебречь, то формулы для j1 и j2 принимают вид:
в знаменателе можно пренебречь, то формулы для j1 и j2 принимают вид:


Задача 6. Тонкий стержень длиной  =10 см равномерно заряжен зарядом q = -3×10-9 Кл. Определите напряженность и потенциал поля в точке С, лежащей на оси стержня. На расстоянии x 0 от середины стержня до этой точки.
=10 см равномерно заряжен зарядом q = -3×10-9 Кл. Определите напряженность и потенциал поля в точке С, лежащей на оси стержня. На расстоянии x 0 от середины стержня до этой точки.
Дано:
x o= 20 см
q = -3. 10—9 Кл
 = 10 см = 10 см
| Решение. Заряд не является точечным, поэтому стержень разбивается на элементарные отрезки dx, заряд dq на которых можно считать точечным. |
| E c —? j c —? | 
|
Потенциал поля, создаваемый в точке С зарядом dq, равен

Потенциал поля, создаваемый в точке С всем стержнем, находится интегрированием

Таким образом,
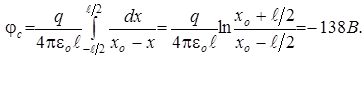
Напряженность поля вдоль оси OX равна
 .
.
Отсюда 
Ответ: φc= -138 В; E c= 720 В/м.
Задача 7. В плоский конденсатор влетает электрон со скоростью V = 2×107 м/c, направленной параллельно пластинам конденсатора. На какое расстояние от своего первоначального направления сместится электрон за время пролета конденсатора? Расстояние между пластинами d = 2 см, длина пластин конденсатора  =5 см, разность потенциалов между пластинами U = 200 В.
=5 см, разность потенциалов между пластинами U = 200 В.
|
|
|
Дано:
V о = 2. 10-7 м/с
d = 2 см = 2. 10-2 м
 = 5 см
U = 200 В
m = 9,1. 10-31 кг
e = 1,6. 10-19 Кл = 5 см
U = 200 В
m = 9,1. 10-31 кг
e = 1,6. 10-19 Кл
| Решение.


|
| S —? |
Движение электрона вдоль оси ОХ является равномерным, вдоль оси ОУ - равноускоренным.

где a – ускорение, приобретаемое электроном под действием силы F = eE. 
Отсюда 
Ответ: S = 5,5 мм.
Задача 8. Плоский воздушный конденсатор с площадью S пластины, равной 500 см2, подключен к источнику тока, ЭДС которого равен 300 В. Определить работу А внешних сил по раздвижению пластин от расстояния d 1 = 1 см до d 3 = 3 см в двух случаях: 1) пластины перед раздвижением отключаются от источника тока; 2) пластины в процессе раздвижения остаются подключенными к нему.
| Дано: S = 500 см2= =5. 10—2 м2 U = 300 B d 1 = 1 см d 3 = 3 см | Решение. Работа внешних сил равна изменению энергии конденсатора: А = W 2 — W 1. 1) Заряд на обкладках конденсатора остается постоянным, так как конденсатор отключен от источника |
| А —? | q = C 1 Dφ = const, где Dφ равна ЭДС источника U. |

2) Пластины остаются подключенными к источнику тока, и система не является изолированной. Заряд с пластин при их раздвижении перемещается к клеммам батареи. В этом случае остается неизменной разность потенциалов между пластинами Dφ = U, поэтому энергию конденсатора удобно представить в виде:  ,
,
тогда  . Таким образом
. Таким образом
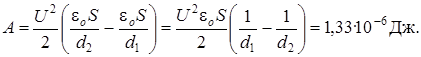
Ответ: 1) А = 3,98·10-6 Дж; 2) A = 1,33·10-6 Дж.
Задача 9. Расстояние d между пластинами плоского конденсатора равно 2 мм, разность потенциалов U = 1,8 кВ. Диэлектрик - стекло. Определите диэлектрическую восприимчивость χ стекла и поверхностную плотность s ¢ связанных зарядов на поверхности стекла.
| Дано: d = 2 мм U = 1,8 кВ e = 7,0 | Решение. e = 1 + χ, χ = e - 1 = 6. s ¢ = Р, где Р — поляризованность диэлектрика. Р = χ eо Е, где Е = U / d — напряженность поля в |
| s ¢—? | диэлектрике. |
Отсюда: s ¢ = χ eо (U / d) = 47,7 . 10—6 Кл/м2.
|
|
|
Ответ: χ = 6, s ¢ = 47,7 . 10—6 Кл/м2.
Задача 10. Плоская квадратная пластина со стороной a =0,1 м находится на некотором расстоянии от бесконечной, равномерно заряженной плоскости (s=1 мкКл/м2). Плоскость пластины составляет угол b=30о с линиями поля. Найти поток Ф вектора электрической напряженности через эту пластину.
| Дано: a = 0.1 м s=1 мкКл/м2 b = 30о | Решение.
 +s +s  a
a
 b
b
|
| Ф —? |
Заряженная плоскость создает однородное электрическое поле с напряженностью  . Таким образом Ф = E·S· cosa.
. Таким образом Ф = E·S· cosa.
Учитывая, что  , окончательно получаем
, окончательно получаем 
Ответ: Ф=280 В·м.
Задача 11. В центре сферы, радиусом R =20 см, находится точечный заряд q =10-2 мкКл. Определить поток вектора напряженности через часть сферической поверхности площадью S =20 см2.
| Дано: R = 20см = 0.2 м q = 10-2 мкКл S = 20см2 = 20·10-4 м2 | 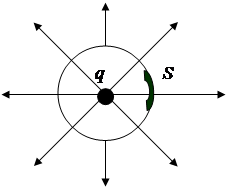 Решение. Решение.
|
| Ф —? |
Поток Ф R через всю сферическую поверхность можно определить по теореме Остроградского-Гаусса: 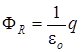 .
.
Искомая часть этого потока, проходящая через S,определяется соотношением  .
.
Ответ: Ф=4,5 В·м.
Постоянный ток
Основные формулы:
Сила тока:  .
.
Плотность тока:  , j = qnV.
, j = qnV.
Закон Ома для однородного участка цепи: 
Сопротивление проводника: 
Зависимость удельного сопротивления от температуры: 
Закон Ома для неоднородного участка цепи: 
Сила тока короткого замыкания:  .
.
Закон Ома для замкнутой цепи:  .
.
Работа электрического поля на участке цепи: 
Закон Джоуля-Ленца: 
Мощность тока: P = I . U.
Полная мощность, выделяемая в цепи: P = I . e.
Первый закон Кирхгофа:  .
.
Второй закон Кирхгофа: 
Примеры решения задач
Задача 12. Амперметр, накоротко присоединенный к источнику тока с ЭДС 1,5 В и внутренним сопротивлением 0,2 Ом, показывает силу тока 5 А. Какую силу тока показывает этот амперметр, если его зашунтировать сопротивлением 0,1 Ом?
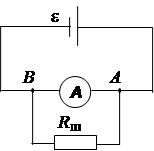 Дано:
e = 1,5 В
r = 0,2 Ом
I 1 = 5 А
R ш = 0,1 Ом Дано:
e = 1,5 В
r = 0,2 Ом
I 1 = 5 А
R ш = 0,1 Ом
| Решение.
Ток в цепи без шунта был равен
 Отсюда Отсюда  .
Ток в цепи с зашунтированным амперметром равен .
Ток в цепи с зашунтированным амперметром равен
| |
| I 2 —? |  , ,
|
где  — сопротивление внешней цепи.
— сопротивление внешней цепи.
Ответ: I 2 = 10 A.
Задача 13. Даны 12 элементов с ЭДС e =1,5В и внутренним сопротивлением r =0,4Ом. При последовательном или параллельном соединении этих элементов в батарею ток внешней цепи, имеющей сопротивление R =0,3 Ом, будет максимальным?
| Дано: n = 12 e = 1,5 В r = 0,4 Ом R = 0,3 Ом | Решение. При последовательном соединении источников тока суммарная ЭДС равна ep= n ×e, а результирующее внутреннее сопротивление батареи равно r p = n . r. Таким образом, ток в цепи при последовательном соединении источников тока равен |
| I max —? | 
|
При параллельном соединении одинаковых источников тока суммарная ЭДС будет равна e, а результирующее внутреннее сопротивление батареи равно  Таким образом, ток в цепи при параллельном соединении источников тока равен
Таким образом, ток в цепи при параллельном соединении источников тока равен 
|
|
|
Ответ: I 2 > I 1 при параллельном соединении.
Задача 14. Электрическая плитка мощностью 1 кВт и нихромовой спиралью предназначена для включения в сеть с напряжением 220 Вт. Сколько метров проволоки диаметром 0,5 мм надо взять для изготовления спирали, если температура нити равна 900оС. Удельное сопротивление нихрома при 0о С — 1мк Ом . м, а температурный коэффициент сопротивления — 4 . 10—4 К—1.
| Дано: Р = 1 кВт = 103 Вт U = 220 В d = 0,5 мм = 0,5.10—3 t = 900о С p o =1мк Ом . м =10—6 Ом . м a = 4 . 10—4 К—1 | Решение.
Мощность плитки равна  где где
 —сопротивление нихромовой проволоки. Сопротивление проволоки также равно —сопротивление нихромовой проволоки. Сопротивление проволоки также равно 
|
 —? —?
| где  — удельное сопротивление проволоки при t =900o C. — удельное сопротивление проволоки при t =900o C.
|
Таким образом, длина нихромовой проволоки, необходимой для изготовления спирали, равна 
Ответ:  =7м.
=7м.
Задача 15. Сила тока в проводнике равномерно нарастает от I o= 0 до I = 3A в течение времени t = 10с. Определить заряд q, прошедший в проводнике.
| Дано: I o = 0 I = 3 A t =10 с | Решение. Элементарный заряд dq, прошедший в проводнике за время dt, равен dq = I · dt, где I в силу равномерного нарастания может быть выражено формулой I = k t, |
| q —? | где 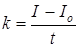 — коэффициент пропорциональности. — коэффициент пропорциональности.
|
Полный заряд, прошедший в проводнике за время t, равен

Ответ: q =15 Кл.
Задача 16. Сила тока в проводнике равномерно нарастает от I o = 0 до некоторого максимального значения в течение времени t =10 с. За это время в проводнике выделилось количество теплоты Q =1 кДж. Определить скорость нарастания тока в проводнике, если сопротивление R его равно 3 Ом.
| Дано: I o = 0 t = 10с Q = 1кДж R = 3 Ом. | Решение.
Количество теплоты, выделившееся в проводнике за время t, равно  , I = k · t,
где , I = k · t,
где  - скорость нарастания тока в проводнике. - скорость нарастания тока в проводнике.
|
| q —? |
 Отсюда
Отсюда 
Ответ: k = 1 A / c.
Задача 17. Три источника тока с ЭДС e1 = 11 B, e2 =4 B и e3 = 6 B и три реостата с сопротивлениями R 1=5 Ом, R 2=10 Ом и R 3=2 Ом соединены, как показано на рисунке. Определить силы токов I в реостатах. Вынужденное сопротивление источника тока пренебрежимо мало.
 Дано:
e1 = 11 B
e2 =4 B
e3 = 6 B
R 1=5 Ом
R 2=10 Ом
R 3=2 Ом Дано:
e1 = 11 B
e2 =4 B
e3 = 6 B
R 1=5 Ом
R 2=10 Ом
R 3=2 Ом
| Решение. | |
| I 1 , I 2 , I 3 —? |
Силы токов в разветвленной цепи определяются с помощью законов Кирхгофа. Поскольку в задаче три неизвестных, необходимо составить три уравнения. Перед составлением уравнений следует, во-первых, выбрать произвольно направления токов, текущих через сопротивления, указав их стрелками на чертеже, и, во-вторых, выбрать направление обхода контуров (только для составления уравнений по второму закону Кирхгофа).
При решении данной задачи направления токов выбраны, как показано на рисунке.
Одно из трех необходимых для решения задачи уравнений составляется, исходя из первого, два других — из второго закона Кирхгофа.
По первому закону Кирхгофа для узла В имеем
I 1 + I 2 - I 3 = 0.
При составлении уравнений по первому закону Кирхгофа необходимо соблюдать правило знаков: ток, подходящий к узлу, входит в уравнение со знаком плюс; ток, отходящий от узла — со знаком минус.
При составлении уравнений по второму закону необходимо соблюдать следующее правило знаков: а) если ток по направлению совпадает с выбранным направлением обхода контуров, то соответствующее произведение IR входит в уравнение со знаком плюс, в противном случае произведение IR входит в уравнение со знаком минус; б) если ЭДС повышает потенциал в направлении обхода контура, то есть, если при обходе контура приходится идти от минуса к плюсу внутри источника, то соответствующая ЭДС входит в уравнение со знаком плюс, в противном случае — со знаком минус.
По второму закону Кирхгофа имеем соответственно для контуров AR 1 BR 2 и AR 2 BR 3 :
I 1 R 1 - I 2 R 2 = e1 - e2,
I 2 R 2 + I 3 R 3 = e2 - e3.
Подставив в уравнения значения сопротивлений и ЭДС, получим систему уравнений:
I 1 + I 2 - I 3 = 0;
5 I 1 - 10 I 2 = 7;
10 I 2 + 2 I 3 = - 2.
Решив эту систему уравнений, получаем что I 1 = 0,8 А, I 2 = - 0,3 А, I 3= 0,5 А.
Знак минус у значения тока I 2 свидетельствует о том, что при произвольном выборе направлений токов, указанных на рисунке, направление тока I 2 было указано противоположно истинному.
Ответ: I 1 = 0,8 А, I 2= - 0,3 А, I 3 = 0,5А.
Магнитное поле в вакууме и веществе
Основные формулы:
Закон Био-Савара-Лапласа:  ,
,
где mо=4p10-7Гн/м.
Магнитная индукция в центре кругового тока:  .
.
Магнитная индукция поля, создаваемого бесконечно длинным прямым проводником с током: 
Магнитная индукция поля,
создаваемого отрезком проводника:


 Связь магнитной индукции с напряженностью магнитного поля:
Связь магнитной индукции с напряженностью магнитного поля: 
Магнитная индукция поля, создаваемого соленоидом в средней его части (или тороида на его оси): 
Принцип суперпозиции магнитных полей: 
Закон Ампера: 
Сила взаимодействия двух прямых бесконечно длинных параллельных проводников с токами: 
Магнитный момент контура с током: Pm = I . S.
Механический момент, действующий на контур с током, помещенный в однородное магнитное поле: M = p m . B sin a.
Сила, действующая на заряд, движущийся в магнитном поле (сила Лоренца): F = q V B sin a.
Закон полного тока: 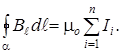
Магнитный поток через плоский контур: Ф = B S cos a.
Потокосцепление, то есть полный магнитный поток, сцепленный со всеми витками соленоида или тороида:  .
.
Магнитный поток сквозь тороид, сердечник которого составлен из двух частей, изготовленных из веществ с различными магнитными проницаемостями: 
Примеры решения задач
Задача 18. Бесконечно длинный тонкий проводник с током I = 50А имеет изгиб (плоскую петлю) радиусом R = 10см. Определить в точке О магнитную индукцию В поля, создаваемого этим током.
| Дано: I = 50А R = 10см | Решение. 
| |
| В —? |
Магнитная индукция в точке О согласно принципа суперпозиции равна  где
где 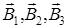 — магнитные индукции поля в точке О, создаваемые током, текущим соответственно на первом, втором и третьем участках проводника.
— магнитные индукции поля в точке О, создаваемые током, текущим соответственно на первом, втором и третьем участках проводника.
Векторы  в соответствии с правилом буравчика направлены перпендикулярно плоскости чертежа в одну сторону (к нам), то есть геометрическое суммирование можно заменить алгебраическим В = В 1 + В 2 + В 3.
в соответствии с правилом буравчика направлены перпендикулярно плоскости чертежа в одну сторону (к нам), то есть геометрическое суммирование можно заменить алгебраическим В = В 1 + В 2 + В 3.
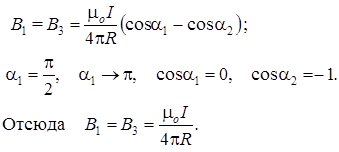
Магнитная индукция В 2 в точке О создается половиной кругового проводника с током, поэтому 
Таким образом, 
Ответ: B =8,05·10-4 Тл.
Задача 19. По двум бесконечно длинным прямым параллельным проводам текут токи I 1 = 20 А и I 2 = 30 А в одном направлении. Расстояние d между проводами равно 10 см. Вычислить напряженность магнитного поля H в точке, удаленной от обоих проводов на одинаковое расстояние r = 10 см.
| Дано: I 1 = 20 А I 2 = 30 А d = 10см r = 10 см | Решение.

| |
| H —? |
Напряженность магнитного поля в точке А согласно принципа суперпозиции равна  .
.  Результирующая напряженность по модулю и направлению является диагональю параллелограмма, построенного на векторах
Результирующая напряженность по модулю и направлению является диагональю параллелограмма, построенного на векторах 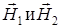
 , где a=60о.
, где a=60о.
Отсюда  .
.
Ответ: H =69,2 А/м.
Задача 20. Провод в виде тонкого полукольца радиусом R = 10 см находится в однородном магнитном поле (В = 50 мТл). По проводу течет ток I =10 А. Найти силу  , действующую на провод, если плоскость полукольца перпендикулярна линиям магнитной индукции, а проводящие провода находятся вне поля.
, действующую на провод, если плоскость полукольца перпендикулярна линиям магнитной индукции, а проводящие провода находятся вне поля.
| Дано: R = 10 см В = 50 мТл = = 50 . 10—3 Тл I = 10 А. | Решение. 
|
| F —? |
Выделим на проводе малый элемент dℓ с током I. На этот элемент тока действует сила Ампера. Направление этой силы определяется по правилу векторного произведения или по правилу левой руки.
Ввиду симметрии провода координатные оси удобно выбрать, как показано на рисунке.

Сила  , действующая на весь провод, равна
, действующая на весь провод, равна  . Из соображений симметрии
. Из соображений симметрии 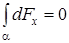 . Тогда
. Тогда  . Так как вектор перпендикулярен вектору
. Так как вектор перпендикулярен вектору  , то dF = JBdℓ.
, то dF = JBdℓ.
Из рисунка видно, что 
Проинтегрировав последнее выражение в пределах от —π/2 до π/2, имеем 
Сила  сонаправлена с единичным вектором
сонаправлена с единичным вектором  .
.
F = 2 I B R = 1 H.
Ответ: F = 1 H.
Задача 21. Электрон в атоме водорода движется вокруг ядра по круговой орбите некоторого радиуса. Найти отношение магнитного момента Рm эквивалентного кругового тока к моменту импульса L орбитального движения электрона. Заряд электрона и его массу считать известными.
| Дано: m = 9,1 . 10—31 кг e = 1,6 . 10—19 Кл | Решение. | |
 Р m / L —? Р m / L —?
|
Эквивалентный круговой ток обусловлен движением электрона по круговой орбите с периодом T.
 ,
,
где V – скорость движения электрона по круговой орбите.
Магнитный момент кругового тока равен
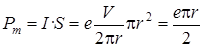 .
.
Момент импульса электрона определяется по формуле L = mVr. Отсюда  .
.
Ответ:  .
.
Задача 22. Электрон движется в однородном магнитном поле с индукцией В =9 мТл по винтовой линии, радиус которой равен 1см и шаг h =7,8 см. Определить период Т обращения электрона и его скорость V.
| Дано: В = 9 мТл R = 1 см h =7,8 см =7,8 . 10-2м m = 9,1 . 10—31 кг e = 1,6 . 10—19 Кл Т —? V —? | Решение.

|
Электрон в магнитном поле движется по винтовой линии под действием силы Лоренца. Вектор скорости V составляет угол a c направлением вектора магнитной индукции  . Электрон движется по окружности радиуса R в плоскости, перпендикулярной линиям индукции со скоростью Vy = V sinα; одновременно он движется и вдоль поля со скоростью
. Электрон движется по окружности радиуса R в плоскости, перпендикулярной линиям индукции со скоростью Vy = V sinα; одновременно он движется и вдоль поля со скоростью  .
.
Уравнение движения электрона по окружности имеет вид  . Отсюда
. Отсюда 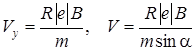 .
.
Шаг винтовой линии h равен пути, пройденному электроном вдоль поля за время, равное периоду обращения электрона Т по окружности h = V x T = V cosα· T, где  . Таким образом
. Таким образом  , и угол a равен
, и угол a равен  .
.
Подставив значение sin a в формулу для скорости u, получаем
V = 2,5 . 107 м/с.
Период обращения электрона Т = 3,97 . 10—9 с.
Ответ: V = 2,5 . 107 м/с, Т = 3,97 . 10—9 с.
Задача 23. Линии напряженности однородного электрического поля и линии индукции однородного магнитного поля взаимно перпендикулярны. Напряженность электрического поля 1 кВ/м, а индукция магнитного поля 1 мТл. Какими должны быть направление и модуль скорости электрона, чтобы его движение было прямолинейным?
| Дано: Е = 1кВ/м =103 В/м В = 1 мТл 10—3 Тл |  Решение. Решение.
| |
| V —? |
На электрон действуют две силы:
1) сила Лоренца 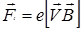 , направленная перпендикулярно скорости
, направленная перпендикулярно скорости  и вектору магнитной индукции
и вектору магнитной индукции  ;
;
2) кулоновская сила  , совпадающая по направлению с вектором напряженности электрического поля.
, совпадающая по направлению с вектором напряженности электрического поля.
По первому закону Ньютона не будет испытывать отклонения при своем движении, если  или eE - eVB =0. Отсюда
или eE - eVB =0. Отсюда  .
.
Ответ: V =106


