 |
Схема вычисления неопределённого интеграла
|
|
|
|
Свойство линейности неопределённого интеграла
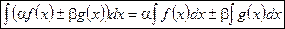
Теорема о замене переменной в неопределённом интеграле

При выборе новой переменной учитывается следующее:
1) Стандартные подстановки
1) В интегралах вида  рекомендуется:
рекомендуется:
если n нечётное, то  ; если m нечётное, то
; если m нечётное, то  ; если и n и m нечётные, то обе подстановки работают, но выгоднее в качестве новой переменной брать ту функцию, степень которой больше (после выбора новой переменной необходимо использовать тригонометрические преобразования для подготовки проведения замены);
; если и n и m нечётные, то обе подстановки работают, но выгоднее в качестве новой переменной брать ту функцию, степень которой больше (после выбора новой переменной необходимо использовать тригонометрические преобразования для подготовки проведения замены);
если n и m чётные, то степени синуса и косинуса понижают по формулам:
 ,
,  ,
,  .
.
2) В интегралах вида  и
и  работают формулы
работают формулы  и
и  .
.
3) В интегралах вида  выбирают
выбирают  ;
;  –
–  ;
;  –
–  . После проведения подстановки при помощи тригонометрических преобразований устраняется иррациональность.
. После проведения подстановки при помощи тригонометрических преобразований устраняется иррациональность.
2. В нестандартной ситуации
рекомендуется в качестве новой переменной выбрать максимально возможное выражение, производная от которого содержится в подынтегральной функции (допускается отличие на числовой коэффициент). Если такого выражения нет, то можно попытаться выбрать в качестве новой переменной наиболее неприятное выражение.
Следствие к теореме о замене переменной в неопределённом интеграле

Интегрирование по частям

Некоторые функции, интегрируемые только по частям, можно классифицировать:
1. Для интегралов вида  рекомендуется в роли u выбрать многочлен
рекомендуется в роли u выбрать многочлен  , а в роли dv – всё остальное. Интегрирование по частям при этом проводится n раз (n – степень многочлена).
, а в роли dv – всё остальное. Интегрирование по частям при этом проводится n раз (n – степень многочлена).
2. Для интегралов вида  рекомендуется в роли dv выбрать
рекомендуется в роли dv выбрать  , а в роли u – оставшуюся функцию.
, а в роли u – оставшуюся функцию.
3. Для интегралов вида  рекомендуется провести интегрирование по частям 2 раза, выбирая в роли u одинаковые функции оба раза, затем решить получившееся уравнение с неизвестным – исходным интегралом.
рекомендуется провести интегрирование по частям 2 раза, выбирая в роли u одинаковые функции оба раза, затем решить получившееся уравнение с неизвестным – исходным интегралом.
|
|
|
Интегрирование рациональных дробей 
1. Если интегрируемая рациональная дробь неправильная  , то нужно разделить многочлен в числителе на многочлен в знаменателе уголком и представить эту дробь в виде суммы многочлена и правильной рациональной дроби
, то нужно разделить многочлен в числителе на многочлен в знаменателе уголком и представить эту дробь в виде суммы многочлена и правильной рациональной дроби  . Затем применить свойство линейности и представить исходный интеграл в виде суммы интегралов от степенных функций и интеграла от правильной дроби.
. Затем применить свойство линейности и представить исходный интеграл в виде суммы интегралов от степенных функций и интеграла от правильной дроби.
2. Чтобы проинтегрировать правильную рациональную дробь нужно:
1) Разложить многочлен знаменателя на множители.
2) Представить дробь в виде суммы простейших в зависимости от множителей знаменателя:
множителю вида  соответствует простейшая дробь
соответствует простейшая дробь  ;
;
множителю вида  соответствует сумма простейших дробей
соответствует сумма простейших дробей  ;
;
множителю вида  , где
, где  соответствует простейшая дробь
соответствует простейшая дробь  .
.
3) Привести полученную сумму простейших дробей к общему знаменателю (равен исходнму знаменателю), приравнять числитель этой дроби к многочлену в числителе исходной правильной рациональной дроби и из этого равенства найти значения неопределённых коэффициентов (для этого рекомендуется в левую и правую части равенства сначала подставить корни знаменателя правильной дроби, затем приравнять коэффициенты при одинаковых степенях х слева и справа).
4) Подставить в интеграл полученное представление дроби с найденными коэффициентами, применить свойство линейности и вычислить интегралы от простейших дробей:
 ,
,  ,
,
а чтобы вычислить интеграл с квадратным трёхчленом нужно разбить его на два так, чтобы первый  вычислялся заменой переменной
вычислялся заменой переменной  , а второй
, а второй  после выделения в знаменателе полного квадрата
после выделения в знаменателе полного квадрата  приобретал табличный вид (9):
приобретал табличный вид (9):

ТЕХНИКА ВЫЧИСЛЕНИЯ НЕОПРЕДЕЛЁННОГО ИНТЕГРАЛА
При вычислении неопределённого интеграла необходимо учитывать, что далеко не все функции можно проинтегрировать аналитически. Окончательный результат получается у табличных интегралов, поэтому основные усилия при вычислении интегралов направлены на придание интегралу табличного вида всеми возможными способами: здесь задействуются элементарные преобразования функций (алгебраические, тригонометрические и т.п.), а также методы замены переменной и интегрирования по частям. Единственное свойство, которым обладает неопределённый интеграл (в отличие от производной) – это свойство линейности: интеграл от суммы равен сумме интегралов, и числовой коэффициент можно выносить за знак интеграла, это свойство также применяется для упрощения вида интеграла.
|
|
|
СХЕМА ВЫЧИСЛЕНИЯ НЕОПРЕДЕЛЁННОГО ИНТЕГРАЛА
1. Сравнить интеграл с таблицей и проанализировать, насколько исходный интеграл отличается от табличных. При этом возможны следующие благоприятные ситуации:
а) интеграл табличный – ответ получается сразу;
б) интеграл отличается от табличного тем, что в подынтегральной функции имеющей табличный вид вместо чистой переменной х представлена её линейная комбинация  , то есть переменная «испорчена» лишь числами – тогда применяется следствие к теореме о замене переменной и результат тоже получается сразу, без дополнительных действий.
, то есть переменная «испорчена» лишь числами – тогда применяется следствие к теореме о замене переменной и результат тоже получается сразу, без дополнительных действий.
В некоторых случаях при проведении анализа выявляется «корень зла» – та ситуация, которую обязательно необходимо устранить, чтобы получить возможность вычислить этот интеграл – тогда дальнейшее действие очевидно; или имеется стандартная ситуация, схема действий в которой тоже определена. В других случаях переходят к пункту 2.
2. Проанализировать, можно ли с помощью элементарных преобразований придать подынтегральной функции табличный вид или представить её в виде суммы и применить свойство линейности, разбив исходный интеграл на сумму более простых.
Перед применением свойства линейности убедиться в его целесообразности: что получаемые при этом интегралы действительно вычисляются легче, чем исходный, или по виду близки к табличным.
3. Оценить возможность применения метода замены переменной или метода интегрирования по частям.
Как правило, в первую очередь нужно попытаться применить метод замены переменной, успех которого зависит от возможности выбора новой переменной.
|
|
|
Достаточно большое количество функций, не подлежащих классификации, интегрируется по частям. Можно рекомендовать сначала подобрать выражение, выступающее в роли dv, так как при вычислении v берётся интеграл  и, чтобы его без труда найти, он должен быть табличным; а в роли u – всё остальное, так как можно легко продифференцировать любую функцию. Часто использование метода интегрирования по частям приводит к решению уравнения, неизвестным в котором выступает исходный интеграл (как в случае класса 3).
и, чтобы его без труда найти, он должен быть табличным; а в роли u – всё остальное, так как можно легко продифференцировать любую функцию. Часто использование метода интегрирования по частям приводит к решению уравнения, неизвестным в котором выступает исходный интеграл (как в случае класса 3).
Следует учитывать, что многие интегралы можно вычислить несколькими способами, поэтому необходимо оценить возможность и уровень сложности процесса применения всех методов, чтобы выявить из них наиболее рациональный.
При вычислении одного интеграла возможно чередование методов или многократное применение одного метода.
ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ
 Формула Ньютона-Лейбница:
Формула Ньютона-Лейбница: 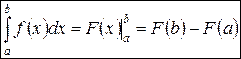 , где
, где  .
.
Геометрический смысл определённого интеграла: 
Вычисление площади плоской фигуры




 для областей первого типа – которые хорошо проецируются на ось Ох;
для областей первого типа – которые хорошо проецируются на ось Ох;

 для областей второго типа – которые хорошо проецируются на ось Оу.
для областей второго типа – которые хорошо проецируются на ось Оу.
ОБЪЁМ ТЕЛА ВРАЩЕНИЯ
Если криволинейная трапеция вращается вокруг оси Ох, то  ,
,
а если вокруг оси Оу, то  .
.
ДЛИНА ДУГИ ПЛОСКОЙ КРИВОЙ
Длина дуги плоской кривой  (
( ) АВ, где
) АВ, где  и
и  вычисляется по формулам:
вычисляется по формулам:  , если
, если  ; или
; или  , если
, если 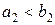 .
.
Если кривая задана параметрически  , то
, то  .
.
ПЛОЩАДЬ БОКОВОЙ ПОВЕРХНОСТИ ТЕЛА ВРАЩЕНИЯ
Если криволинейная трапеция вращается вокруг оси Ох, то 
|
|
|


